Die Scheitelpunktform
Betrachtet man erneut die Übung zur Verschiebung der Parabel in \(x\)- und \(y\)-Richtung, so erkennt man insbesondere, dass die Werte \(x_s\) und \(y_s\), die man am Schieberegler einstellt, den Koordinaten des Scheitelpunkts der Parabel entsprechen. Dies führt zu folgender alternativen Darstellung quadratischer Funktionsterme:
Definition: Scheitelpunktform
Die Darstellung quadratischer Funktionen \(f(x)=a(x-x_s)^2+y_s\) heißt Scheitelpunktform der Funktion \(f\). Hierbei geben die Werte \(x_s\) und \(y_s\) die Koordinaten des Scheitelpunkts an, es gilt also \(S(x_s|y_s)\). Sämtliche Eigenschaften des Leitkoeffizienten a bleiben hierbei von der allgemeinen Form erhalten.
Aufgabe 1
Ermitteln Sie anhand der gegebenen Funktionsgleichungen möglichst viele Informationen über die zugehörigen Funktionsgraphen (Öffnungsrichtung und -weite, Scheitelpunkt):
| a) \(f(x)=(x-3)^2+2\) | b) \(g(x)=\frac12 (x+1)^2+1\) |
| c) \(h(x)=-2 x^2+0,5\) | d) \(i(x)=2 (x-2,5)^2\) |
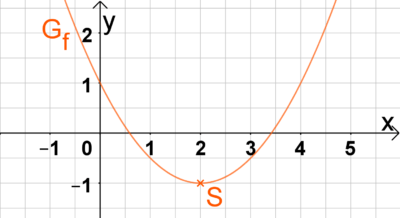 Mit Hilfe der Scheitelpunktform kann man aus einem Funktionsgraphen schnell die zugehörige Funktionsgleichung bestimmen, vorausgesetzt der Scheitelpunkt besitzt Koordinaten, die gut ablesbar sind. Für den nebenstehenden Funktionsgraphen folgt beispielsweise mit dem Scheitelpunkt \(S(2|-1)\):
Mit Hilfe der Scheitelpunktform kann man aus einem Funktionsgraphen schnell die zugehörige Funktionsgleichung bestimmen, vorausgesetzt der Scheitelpunkt besitzt Koordinaten, die gut ablesbar sind. Für den nebenstehenden Funktionsgraphen folgt beispielsweise mit dem Scheitelpunkt \(S(2|-1)\):
\[f(x)=a(x-2)^2-1\]
Um den Leitkoeffizienten zu bestimmen genügt es nun einen weiteren Punkt auf dem Funktionsgraphen in die gefundene Funktionsgleichung einzusetzen und nach \(a\) aufzulösen. Hier bietet sich z.B. der Punkt \(P(0|1)\) an. Man erhält:
\[\begin{array}[lllll]\hspace 1&=&a(0-2)^2-1&\\1&=&a(-2)^2-1&\\1&=&4a-1&\vert +1\\2&=&4a&\vert :4\\\frac12&=&a&\end{array}\]
Folglich lautet die Funktionsgleichung der Funktion \(f\):
\[f(x)=\frac{1}{2} (x-2)^2 -1\]
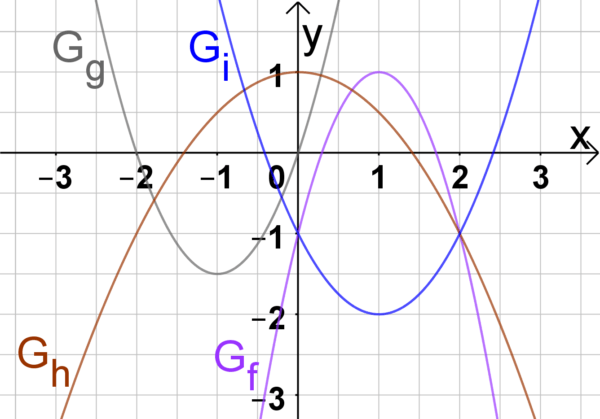
Aufgabe 2
Bestimmen Sie zu den gegebenen Graphen jeweils die Scheitelpunktform.