Preisbildung auf dem vollkommenen Markt
Angebot und Nachfrage
Das Verhalten von Angebot und Nachfrage auf Preisänderungen wurde bisher einzeln untersucht. Der Preis bildet sich aus dem Zusammenwirken beider Faktoren. Folgende Darlegungen gelten für die Bedingungen des vollkommenen Marktes, der z.B. an der Wertpapierbörse gegeben ist. Die Wertpapierhändler erhalten von den Käufern und Verkäufern Kauf- oder Verkaufsaufträge. Dabei können Käufer und Verkäufer ihre Aufträge limitieren. Ein Käufer könnte den Börsenmakler beauftragen, ein bestimmtes Wertpapier zu höchstens 72,00 € pro Stück zu kaufen. Sollte der Kurs an diesem Tag höher sein, wird der Auftrag nicht ausgeführt. Ein Verkäufer kann den Börsenmakler beauftragen, ein Wertpapier zu mindestens 71,00 € zu verkaufen. Ist der Kurs am Verkaufstag niedriger, wird der Auftrag nicht ausgeführt. Werden die Kauf- und Verkaufsaufträge nicht limitiert, so werden die zum Kauf nachgefragten Wertpapiere „billigst“ und die zum Verkauf angebotenen Wertpapiere „bestens“, d.h. zu dem am Abschlusstag gültigen Kurs gekauft oder verkauft.
Bei einem Wertpapierhändler laufen folgende Aufträge ein:
| Kaufaufträge (Nachfrage) | Verkaufsaufträge (Angebot) |
| Käufer A: 50 Stück billigst | Verkäufer F: 30 Stück bestens |
| Käufer B: 45 Stück zu 71,00 € höchstens | Verkäufer G: 45 Stück zu 71,00 € mindestens |
| Käufer C: 20 Stück zu 72,00 € höchstens | Verkäufer H: 65 Stück zu 72,00 € mindestens |
| Käufer D: 40 Stück zu 73,00 € höchstens | Verkäufer I: 120 Stück zu 73,00 € mindestens |
| Käufer E: 30 Stück zu 74,00 € höchstens | Verkäufer J: 140 Stück zu 74,00 € mindestens |
Der Makler hat nun die Aufgabe festzustellen, bei welchem Kurs der höchste Umsatz erzielt werden kann. Dazu muss festgestellt werden, welche Umsätze bei den einzelnen Preisen möglich sind:
| Mögliche Preise | Durchführbare Kaufaufträge (in Stück) |
Durchführbare Verkaufsaufträge (in Stück) |
Umsatz (mögliche Menge · Preis) |
| 70,00 € | 50 + 45 + 20 + 40 + 30 = 185 | 30 | 30 · 70,00 = 2.100,00 € |
| 71,00 € | 50 + 45 + 20 + 40 + 30 = 185 | 30 + 45 = 75 | 75 · 71,00 = 5.325,00 € |
| 72,00 € | 50 + 20 + 40 + 30 = 140 | 30 + 45 + 65 = 140 | 140 · 72,00 = 10.080,00 € |
| 73,00 € | 50 + 40 + 30 = 120 | 30 + 45 + 65 + 120 = 260 | 120 · 73,00 = 8.760,00 € |
| 74,00 € | 50 + 30 = 80 | 30 + 45 + 65 + 120 + 140 = 400 | 80 · 74,00 = 5.920,00 € |
In diesem Beispiel beträgt der vom Makler festgesetzte Preis 72,00 €, weil hier die angebotene Menge der nachgefragten Menge entspricht. Man spricht vom Gleichgewichtspreis. Zu beachten ist, dass die Anbieter, die einen höheren Preis erzielen wollten, und die Nachfrager, die nur einen geringeren Preis bezahlen wollten, leer ausgehen.
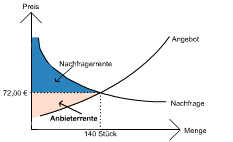
Nachfragerrente (Konsumentenrente): Es gibt Käufer, die mehr ausgegeben hätten als den zustande gekommenen Preis. Die Konsumentenrente stellt als Ersparnis die Differenz zwischen der maximalen Zahlungsbereitschaft und dem tatsächlichen Preis dar.
Anbieterrente (Produzentenrente): Manche Verkäufer erhalten durch den ermittelten Gleichgewichtspreis mehr als sie ursprünglich für den Verkauf einnehmen wollten. Die Produzentenrente stellt einen zusätzlichen Erlös dar.
Der Gleichgewichtspreis ergibt sich aus der Schnittstelle zwischen der Angebots- und der Nachfragekurve. Liegt der Preis über 72,00 €, so wollen die Anbieter mehr verkaufen, als die Konsumenten gewillt sind zu kaufen. Das Ergebnis ist ein Angebotsüberhang. Bei einem niedrigeren Preis als 72,00 € entsteht auf dem Markt eine Fehlmenge, die dann durch ein Ansteigen der Preise ausgeglichen wird. Bei einem Preis von 72,00 € entstehen weder Fehlmengen noch Angebotsüberhänge. Der Konsument, der 40 Stück zu höchstens 73,00 € kaufen wollte, erzielt eine Konsumentenrente von 40 * (73 – 72) = 40,00 €. Der Anbieter, der bereit war 45 Stück zu 71,00 € zu verkaufen, erzielt damit eine Produzentenrente von 45 * (72 – 71) = 45,00 €.
Preisbildung auf dem vollkommenen Markt: Aufgaben
Testen Sie Ihr Wissen an folgenden Beispielen:
An der Wertpapierbörse gehen folgende Aufträge für die X-Aktie ein:
| Käufer | Nachgefragte Menge | Kurswunsch (höchstens) | Verkäufer | Angebotene Menge | Kurswunsch (mindestens) | |
| A | 30 | billigst | F | 40 | bestens | |
| B | 6 | 34,00 € | G | 14 | 31,00 € | |
| C | 8 | 33,00 € | H | 12 | 32,00 € | |
| D | 22 | 32,00 € | I | 25 | 33,00 € | |
| E | 14 | 31,00 € | J | 30 | 34,00 € |
Aufgaben:
1 Ermitteln Sie rechnerisch den Gleichgewichtspreis.
2 In welcher Höhe erzielen die Marktteilnehmer B, E, G und I welche Art von „Rente“?
3 Erklären Sie, weshalb sich der Preis auf dem vollkommenen Markt im Schnittpunkt von Angebot und Nachfrage einpendelt. Erklären Sie, was passiert, wenn sich der Marktpreis als zu hoch oder zu niedrig erweist.
