Preisbildung im unvollkommenen Polypol
Beschreibung der Marktform
Das Marktmodell des unvollkommenen Polypols ist in der Realität häufig anzutreffen. Im unvollkommenen Polypol ist mindestens eine der Bedingungen des vollkommenen Marktes nicht erfüllt. Auf realen Märkten fehlt es zumeist sogar an mehreren Erfordernissen. Andere Bezeichnungen für dieses Marktmodell sind monopolistischer Wettbewerb oder heterogene Konkurrenz.
Der monopolistische Wettbewerb unterscheidet sich vom vollkommenen Polypol vor allem durch folgende Merkmale:
- Auf einem unvollkommenen Markt werden nicht homogene, sondern heterogene Güter angeboten.
- Die Unternehmen versuchen durch das absatzpolitische Instrumentarium wie Werbung oder Produktgestaltung Präferenzen der Nachfrager für bestimmte Produkte zu wecken.
- Es stehen sich viele Anbieter und viele Nachfrager mit jeweils geringen Marktanteilen gegenüber.
- Ein einheitlicher Preis kommt nicht zustande.
Obwohl infolge der vielen Anbieter Wettbewerb herrscht, hat der einezlne Anbieter aber auch einen gewissen preispolitischen Spielraum, innerhalb dessen er, wie ein Monopolist, seinen Preis beliebig festsetzen kann.
Wird das Nachfrageverhalten grafisch abgebildet, ergibt sich eine doppelt geknickte Preis-Absatz-Funktion. Zwischen der Preisobergrenze (p1) und der Preisuntergrenze (p2) ist die Nachfrage relativ unelastisch. Eine Preiserhöhung führt in diesem Bereich nur zu einem geringeren Nachfragerückgang. Bei Preissteigerungen über p1 hinaus, verliert der Anbieter jedoch alle Nachfrager. Setzt der Anbieter den Preis zu niedrig fest, wechseln alle Nachfrager aufgrund des günstigen Angebots zu ihm über. Aber da sein Marktanteil zu gering ist, kann er diese Nachfrage nicht befriedigen.
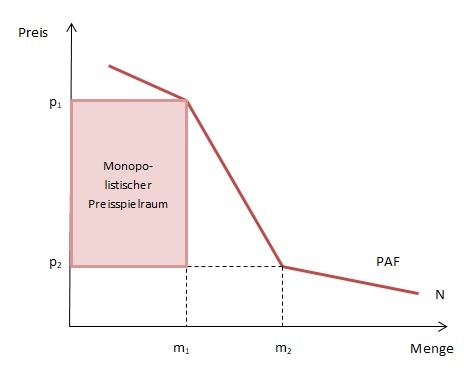
Da der einzelne Anbieter nur einen ganz geringen Marktanteil hat, kann er das Marktgeschehen insgesamt kaum beeinflussen. Auf seine Maßnahmen (z. B. Preiserhöhung) werden daher die anderen Anbieter auch kaum reagieren. Der Anbieter im unvollkommenen Polypol muss daher bei seinen Aktionen in erster Linie das voraussichtliche Verhalten der Nachfrager und weniger die Gegenmaßnahmen der Konkurrenten berücksichtigen. Überschreiten Preisänderungen nach oben oder unten die von den Nachfragern hingenommenen Grenzen, so reagieren sie mit starken Nachfrageänderungen.
Die Größe des monopolistischen Preisspielraums hängt – neben der Standortdichte der Anbieter und der Elastizität der Nachfrage – vor allem von den Substitutionsverhältnissen ab, d. h. von der Bereitschaft der Nachfrager, bei Preiserhöhungen auf ein vergleichbares Gut eines anderen Anbieters auszuweichen. Daher lassen sich die untere und obere Grenze des monopolistischen Preisspielraums auch als Substitutionsschwelle bezeichnen. Überschreitet ein Anbieter diese Schwelle, sind die Nachfrager zur Substitution bereit. Die Anbieter sind daher bemüht, mittels Werbung eine intensive Produktdifferenzierung zu betreiben, die ihr Gut in den Augen der Nachfrager deutlich von den (ähnlichen) Produkten anderer Anbieter abhebt. Je mehr dies gelingt, umso höher liegt die Schwelle der Abwanderung.
Beispiel
Eine kleine Bäckerei bietet montags bis freitags am Mittag ein warmes Essen an. Die Bäckerei möchte für dieses Angebot ihren Gewinn maximieren. Eine intensive Marktforschung hat die in der Tabelle dargestellten Preis-Mengen-Kombinationen und folgende Preis-Absatz-Funktion ermittelt:
für m < 200: p = 8
für 200 <= m <= 800: p = 10 – 0,01 m
für m > 800: p = 2
Für das warme Mittagessen musste die Bäckerei investieren. Es fallen monatlich fixe Kosten von 350,00 € an. Die variablen Kosten für das Essen betragen 1,10 € pro Mahlzeit. Der Bäckerei ist es nicht möglich, mehr als 800 Essen pro Monat zu kochen.
| Menge in Stück |
Preis in € |
Erlös je Monat in € |
Kosten je Monat in € |
Gewinn/Verlust je Monat in € | Grenzerlös je Stück in € | Grenzkosten je Stück in € |
| 0 | 8,00 | 0,00 | 350,00 | – 350,00 | 8,00 | 1,10 |
| 100 | 8,00 | 800,00 | 460,00 | 340,00 | 8,00 | 1,10 |
| 200 | 8,00 | 1.600,00 | 570,00 | 1.030,00 | 6,00 | 1,10 |
| 300 | 7,00 | 2.100,00 | 680,00 | 1.420,00 | 4,00 | 1,10 |
| 400 | 6,00 | 2.400,00 | 790,00 | 1.610,00 | 2,00 | 1,10 |
| 500 | 5,00 | 2.500,00 | 900,00 | 1.600,00 | 0,00 | 1,10 |
| 600 | 4,00 | 2.400,00 | 1.010,00 | 1.390,00 | – 2,00 | 1,10 |
| 700 | 3,00 | 2.100,00 | 1.120,00 | 980,00 | – 4,00 | 1,10 |
| 800 | 2,00 | 1.600,00 | 1.230,00 | 370,00 | – 6,00 | 1,10 |
| 900 | 2,00 | 1.800,00 | 1.340,00 | 460,00 | 2,00 | 1,10 |
| 1.000 | 2,00 | 2.000,00 | 1.450,00 | 550,00 | 2,00 | 1,10 |
| 1.100 | 2,00 | 2.200,00 | 1.560,00 | 640,00 | 2,00 | 1,10 |
Der Grenzerlös stellt jenen zusätzlichen Erlös dar, welcher durch den Verkauf einer zusätzlichen Mengeneinheit erzielt werden würde. Er ist abhängig vom Verlauf der Nachfragefunktion. Grenzkosten sind die Kosten, die entstehen, wenn man eine Einheit eines Produktes mehr herstellt. Spiegelbildlich formuliert, sind es die Kosten, die entstehen, wenn man ein Stück weniger produziert. Die Grenzkosten entsprechen in der Regel den variablen Kosten. Der Grenzerlös bezieht sich ebenso wie die Grenzkosten auf eine zusätzlichen Produkteinheit, also auf ein einzelnes Stück.
Für die Erlösfunktion gilt:
für m < 200: E = 8 m
für 200 <= m <= 800: E = 10 m – 0,01 m2
für m > 800: E = 2 m
Der Grenzerlös ist damit:
für m < 200: E‘ = 8
für 200 <= m <= 800: E‘ = 10 – 0,02 m
für m > 800: E’= 2
Für die Gesamtkosten gilt: Kg = 350 + 1,10 m
Die Grenzkosten sind damit: Kg‚ = 1,10
Das Gewinnmaximum ermittelt sich bei der Menge im monopolistischen Bereich, bei der die Grenzkosten den Grenzerlösen entsprechen:
1,10 = 10 – 0,02 m
m = 445 Stück
Der Preis ist dann:
p = 10 – 0,01 * 445 = 5,55 €
Der maximale Gewinn beträgt dann:
G = E – Kg = p * m – Kf – Kv = 5,55 * 445 – 350 – 1,1 * 445 = 1.630,25 €
Der Bäcker erzielt bei den Mittagessen sein Gewinnmaximum bei einem Preis von 5,55 € pro Essen. Er kann im Monat 445 Stück verkaufen und erwirtschaftet einen Gewinn von 1.630,25 €.
Dies lässt sich grafisch darstellen. In der Gesamtbetrachtung:
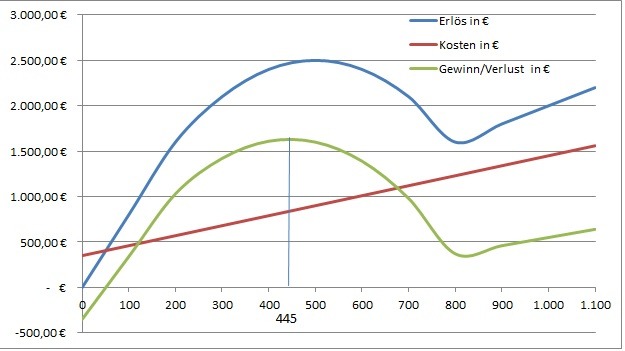
und in der Stückbetrachtung:
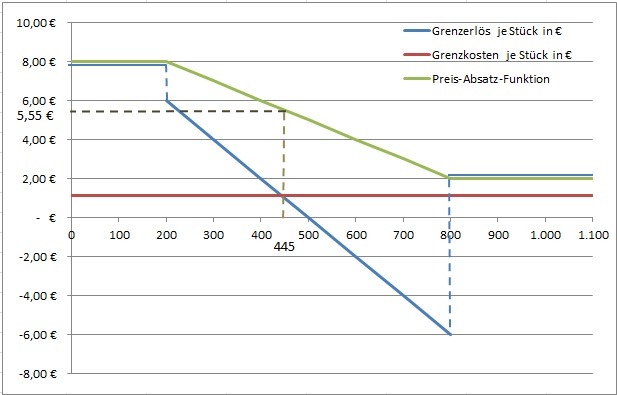
Preisbildung im unvollkommenen Polypol: Aufgaben
Testen Sie Ihr Wissen an folgenden Beispielen:
Sie sind Mitarbeiter der RUSEL AG, einem industriellen Hersteller von Autoreifen mit eigenem Vertrieb. Trotz großer Konkurrenz will die RUSEL AG in der nächsten Wintersaison einen neuen Winterreifen auf den Markt bringen. Für ihr neues Produkt geht die Geschäftsleitung der RUSEL AG, anlog zur Konkurrenz, von einem geringen Marktanteil aus.
Ein von der RUSEL AG beauftragtes Marktforschungsinstitut liefert bezüglich preispolitischer Aktivitäten für das neue Produkt folgende Informationen:

Weiterhin sind Ihnen aus Ihrer Abteilung folgende Daten bekannt:
Die monatliche Kostenfunktion für die Herstellung des neuen Winterreifens lautet (Werte in €): K = 40,00 x + 50.000,00
Die maximale Kapazität der zur Produktion verwendeten Anlage beträgt 2.500 Stück/Monat.
Sie erhalten von der Geschäftsleitung der RUSEL AG den Auftrag, für den neuen Winterreifen den gewinnmaximalen Preis festzulegen und grafisch zu veranschaulichen.
Aufgaben:
1 Begründen Sie, auf welchem Markt (Marktform, Vollkommenheit) die RUSEL AG mit ihren Autoreifen tätig ist.
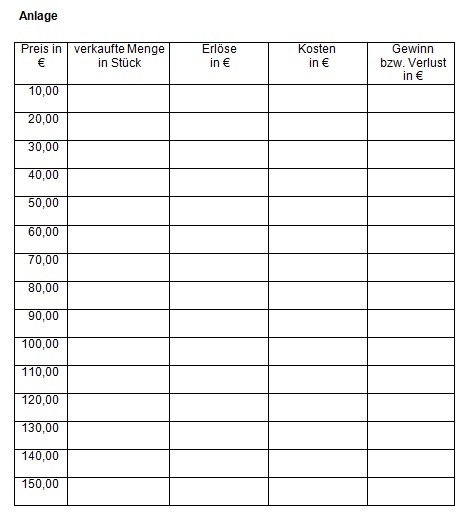
2 Beschaffen Sie sich die notwendigen Informationen zur Festlegung des gewinnmaximalen Preises. (Anlage 1)
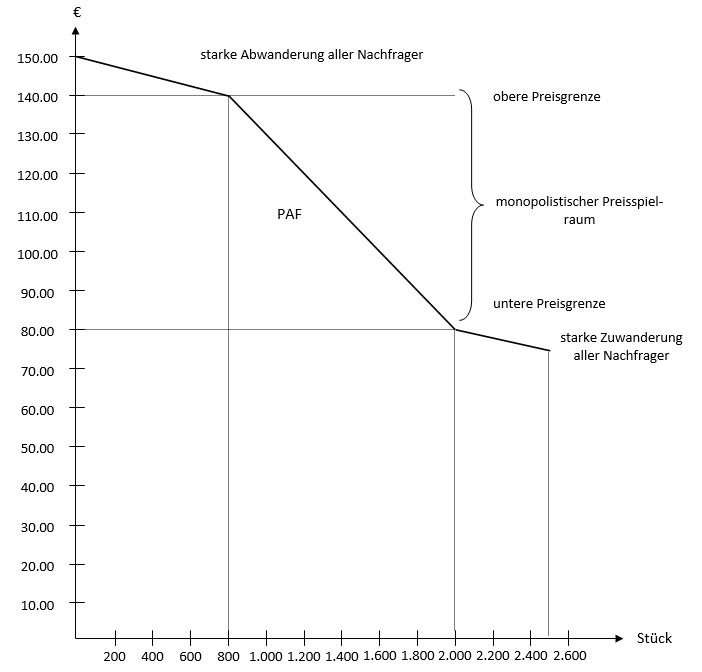
2.1 Stellen Sie die vom Marktforschungsinstitut zur Verfügung gestellten Daten in einer vollständig beschrifteten Grafik dar. (x-Achse: 1cm = 200 Stück; y-Achse: 1cm = 10,00 €)
2.2 Berechnen Sie die direkte Preiselastizität der Nachfrage für folgende Preisveränderungen:
Preiserhöhung von
(1) 140,00 € auf 150,00 €
(2) 80,00 € auf 90,00 €
Preissenkung von
(3) 80,00 € auf 70,00 €
2.3 Analysieren Sie u. a. mit Hilfe der berechneten Elastizitäten (vgl. 2.2) und der erstellten Grafik (vgl. 2.1) die Preisgestaltungsmöglichkeiten der RUSEL AG bzw. das Nachfrageverhalten nach dem neuen Winterreifen für folgende Preise bzw. Preisintervalle.
p = 150,00 €
150,00 € > p > 140,00 €
140,00 € >= p >= 80,00 €
p < 80,00 €
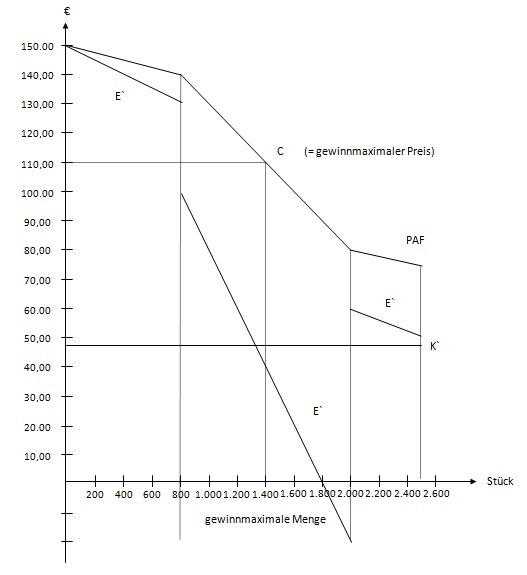
3 Ermitteln Sie die gewinnmaximale Preis-Mengen-Kombination der RUSEL AG.
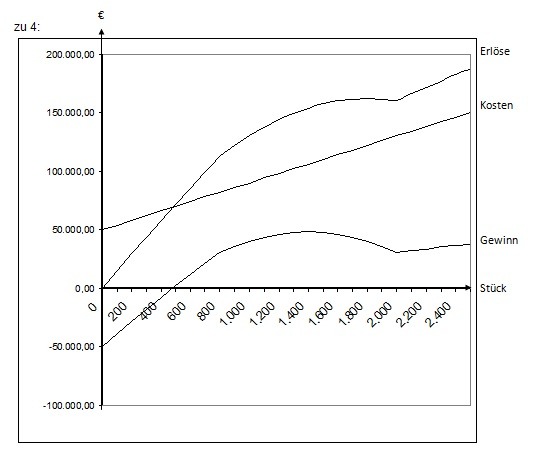
4 Veranschaulichen Sie die Situation mit Hilfe einer Grafik. Stellen Sie hierzu die Erlöse, die Kosten und den Gewinn dar.
5 Die Unternehmensleitung der RUSEL AG wählt für den neuen Winterreifen die gewinnmaximale Preis-Mengen-Kombination. Erläutern Sie jeweils eine mögliche Konsequenz dieser Preisfestsetzung für die Arbeitnehmer der RUSEL AG und der Nachfrager.
6 NEUE Ausgangssituation: Sie helfen ehrenamtlich beim Open Air Kino „SummerNights“ in Ihrer Stadt mit. Das Open Air Kino befindet sich am Stadtrand und fand in den letzten Jahren großen Zuspruch. Um weiterhin möglichst viele Besucher zu gewinnen, hat man beschlossenen, dass sich die Besucher Essen und Getränke von zu Hause mitnehmen dürfen. Der Eishändler Müller verkauft Zitroneneis am Stiel auf dem Open Air Gelände. Erfahrungsgemäß können bei einem Preis 1,60 Euro je Eis 220 Stück verkauft werden. Dies entspricht auch aufgrund beschränkter Kühlmöglichkeiten der maximal möglichen Verkaufsmenge des Eishändlers, auch wenn er noch weitere 80 Stück zu diesem Preis verkaufen könnte. Wenn der Eishändler Müller den Preis auf 4,00 Euro je Eis erhöht, dann kann er noch 115 Stück verkaufen. Der Prohibitivpreis liegt bei 4,20 Euro je Eis. In der Nähe des Open Air Kinos verkaufen einige Tankstellen und relativ viele Supermärkte ebenfalls das Zitroneneis.
6.1 Begründen Sie, weshalb es sich im vorliegenden Fall „Zitroneneismarkt“ um ein Polypol sowie um einen unvollkommenen Markt handelt.
6.2 Skizzieren Sie die für den Eishändler Müller geltende Preis-Absatz-Funktion und erläutern Sie die aus Ihrer Skizze ersichtlichen preispolitischen Bereiche.
6.3 Erläutern Sie den Unterschied zwischen der Preis-Absatz-Funktion eines Anbieters und der Gesamtnachfragekurve nach dem Gut.
Hier finden Sie die Anlagen zu den Aufgaben: