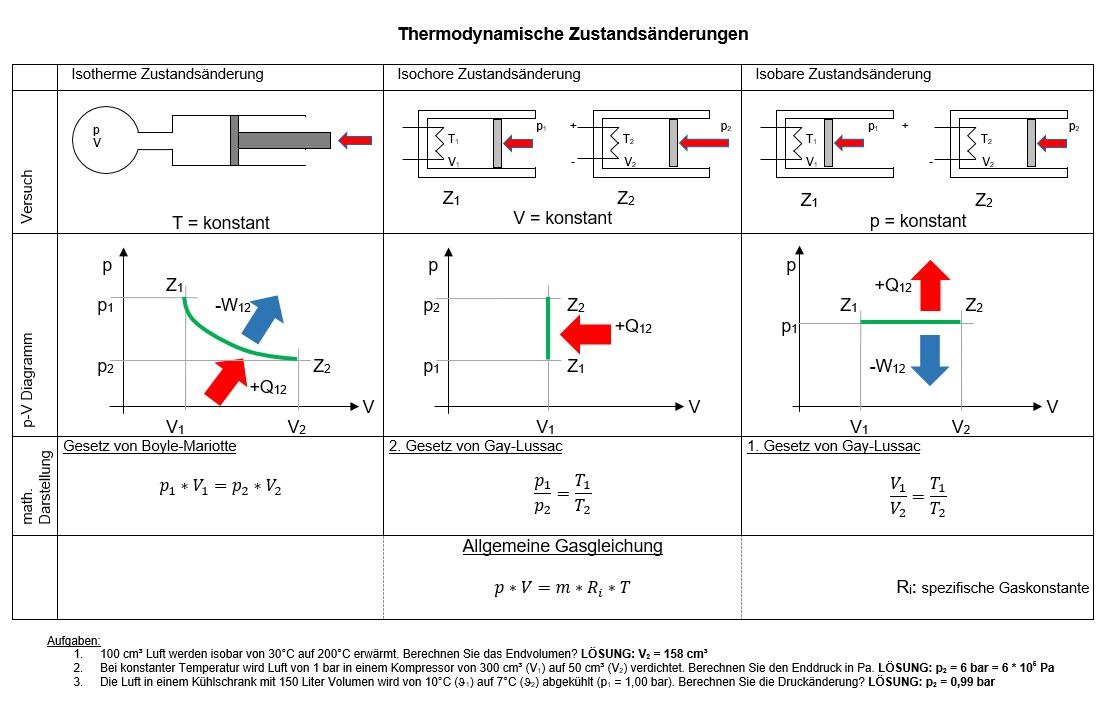
Energie und Arbeit
Der Betrachtung der umgesetzten Energie bei den Zustandsänderungen bedarf der genauerer Betrachtung. Bei einer Zustandsänderung kann je nach System Stoff bzw. Materie und Energie umgesetzt werden. Bei den bisher betrachteten geschlossenen Systemen wird nur Energie mit der Umgebung ausgetauscht. Die Energie kann dabei mechanisch Arbeit oder Wärmeenergie sein.
Mechanische Arbeit
Bei den isobaren und isochoren Prozessen zeigte sich, dass die während des Prozesses umgesetzte Arbeit dem Flächeninhalt der unter der Prozesskurve p(V) liegenden Fläche entspricht. Diese Erkenntnis gilt für beliebige Prozesse. Man erkennt das daran, weil ein beliebiger Prozessverlauf durch eine Folge von isobaren und isochoren Prozessen angenähert werden kann.
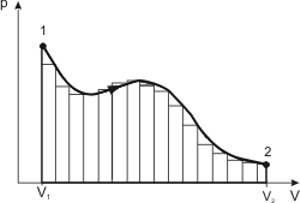
Um die bei einem Prozess umgesetzte Arbeit zu berechnen, muss also lediglich der Inhalt der unter der Prozesskurve p(V) liegenden Fläche berechnet werden. Das kann numerisch geschehen, indem die Fläche in kleine Rechteckstreifen unterteilt wird. Die Teilflächeninhalte der Rechteckstreifen werden einzeln berechnet, anschließend werden die Teilinhalte aufsummiert. Diese Methode kann sehr gut mit Hilfe eines Computers durchgeführt werden. Aber auch die Mathematik hat eine leistungsfähige Methode entwickelt, um solche Flächeninhalte zu berechnen, gemeint ist die Integralrechnung. Voraussetzung für ihre Anwendung ist, dass der Druck als Funktion des Volumens bekannt ist, was nur bei einfachen Prozessen der Fall ist. Mit der Symbolik der Integralrechnung kann das Problem der Arbeitsberechnung elegant formuliert werden. Für die Arbeit W12 eines beliebigen Prozesses gilt:
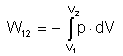
Diese Formel besagt eigentlich nur, dass zur Ermittlung der Arbeit W12 der Inhalt der unter der Prozesskurve liegenden Fläche zu berechnen ist. Die Methode ist Sache der Mathematik. Das Minuszeichen vor dem Integral wird benötigt, um das richtige Vorzeichen für zu- bzw. abgeführte Arbeit zu erhalten. Wie bereits bekannt ist, erhält die Arbeit ein negatives Vorzeichen, wenn Arbeit abgegeben wird, also bei einer Expansion des Gases. Hingegen ist das Vorzeichen bei zugeführter Arbeit, d.h. bei einer Kompression, positiv. Es gilt:
W12 = – W12
Bei thermodynamischen Prozessen entspricht also die umgesetzte Arbeit dem Betrage nach dem Flächeninhalt unter der Prozesskurve.
Wärmeenergie (Thermische Energie)
In einem idealen Gas bewegen sich die Gasmoleküle. Diese Beobachtung der allgemeinen Wärmebewegung geht auf den britischen Botaniker Robert Brown (1827) zurück, der Brown’schen Molekularbewegung, diese lässt sich leicht in Flüssigkeiten zeigen [Video]. Die Moleküle bewegen sich dabei ungeordnet und besitzen damit sowohl kinetische als auch potentielle Energie. Bei hohen Temperaturen bewegen sich die Moleküle schneller als bei niedrigen Temperaturen. Die thermische Energie Eth kann also durch Wärmezufuhr erhöht und durch Wärmeabfuhr erniedrigt werden. Der Zusammenhang von Temperatur T und thermischer Energie ist bei idealen Gasen nahezu proportional.
Eth ~ T
Die thermische Energie ist damit aber auch zur zugeführten Wärme Q proportional, da
Q = m * c * T
Die stoffabhängige Größe in dieser Gleichung ist die spezifische Wärmekapazität c. Die spezifische Wärmekapazität ist allerdings von der Temperatur abhängig. Sie beschreibt, in welchem Maß eine Stoff Wärme speichern kann. In der Tabelle sind einige spezifische Wärmekapazitäten angegeben (bei 20°C). Desweiteren muss bei der Berechnung der Wärme die Art der Zustandsänderung berücksichtigt werden, bei einer isobaren Zustandsänderung (cp) wird Wärme und Arbeit umgesetzt, bei einer isochoren (cV) nur Wärme.
| Gas | cp in kJ/kgK | CV in kJ/kgK |
| Wasserstoff | 14,32 | 10,17 |
| Helium | 5,193 | 3,21 |
| Methan | 2,158 | 1,696 |
| Butan | 1,658 | |
| Neon | 1,030 | 0,628 |
| Luft | 1,005 | 0,717 |
| Argon | 0,523 | 0,317 |
Innere Energie
In der Einleitung zu dem Lernbereich Thermodynamik wurden die Zustandsgrößen Druck, Temperatur und Volumen vorgestellt. Die Zustandsgrößen lassen sich in extensive und intensive Größen unterscheiden. Zu den Merkmalen der extensiven Größen gehört, dass sie sich mit der Größe (Raum) des betrachteten Systems verändern. Das Volumen aber auch die Masse oder die Stoffmenge sind extensive Größen. Verändert sich die Größe nicht, spricht man von intensiven Größen, wie der Temperatur, dem Druck und der im System steckenden Energie.
Mechanische Arbeitszu- oder abfuhr und die Änderung der thermischen Energie während einer Zustandsänderung verändert die im System enthaltene, gespeicherte Energie. Diese Energie wird als innere Energie U bezeichnet. Die innere Energie lässt sich bei der isochoren Zustandsänderung gut veranschaulichen. Einem geschlossenen System wird bei gleichbleibendem Volumen Energie (Wärme Q12) zugeführt. Diese Energie steckt jetzt als erhöhte innere Energie U als erhöhte Temperatur und erhöhtem Druck im System, sie ist nicht verloren gegangen – das wäre ein Widerspruch zum Energieerhaltungssatz. Es gilt
U = Q12
Die umgesetzten Energien bei den einzelnen Zustandsänderungen sind in der Lösung zum Arbeitsblatt Zustandsänderungen eingetragen. Ändert sich die Richtung der Zustandsänderung, z.B. von der isothermen Expansion zur isothermen Kompression, so ändern sich die Vorzeichen der umgesetzten Energien.