Kraftübertragungprinzipien

Werden Bauteile freigeschnitten, so entstehen Gegenkräfte, bzw. die Gegenkräfte werden sichtbar gemacht. Um die Gegenkräfte möglichst einfach zu erfassen, wird auf grundlegende Kraftübertragungsprinzipien zurückgegriffen. Gegenkräfte wurden in der Architektur des 19. Und 20. Jahrhundert gerne ‚sichtbar‘ gemacht. Dabei wurde auf die griechische Mythologie zurückgegriffen, auf den Titanen Atlas, der das Himmelsgewölbe stützen musste. Steingeworden Titanen stützen noch heute Brückenpfeiler, Erker, Dächer, …

Auch wenn Atlas heute die Physik nicht mehr stützt, bietet doch die Vorstellung ‚Ich muss dieses Teil (Erker, Brücke) halten – welche Gegenkräfte muss ich dafür aufbringen‘ eine brauchbare Anschauung.

Seil

Ein Seil kann nur eine Kraft in Seilrichtung übertragen, beim Freischneiden tritt somit nur eine Gegenkraft F_S in Seilrichtung auf (Freischneiden). Bei durchhängenden Seilen (Funktion F_s(x)) ist die Richtung der Seilkraft die Steigung der dazugehörenden Funktion.

Stab

Ein Stab kann sowohl Kräfte in Längs- als auch in Querrichtung übertragen. Diese werden als Normal- und Querkräfte bezeichnet und sind aufgrund ihrer unterschiedlichen maximal zulässigen Größen als Einzelkräfte bei der Bauteildimensionierung zu bestimmen.

1-wertiges Lager

Ein 1-wertiges Lager kann nur Kräfte in einer Richtung aufnehmen. Als Beispiel ist das schon erwähnte Seil zu nennen und die sogenannte Pendelstütze (fester Stab, drehbar gelagert). 1-wertige Lager finden sich häufig als Auflager für Brücken, das Lager stützt die Brücke dabei nur nach unten hin ab, nach rechts und links kann sich die Brücke frei bewegen, ebenso kann sie um das Lager L gedreht werden. Das Seil kann nur Zugkräfte aufnehmen, der Pendelstutzen sowohl Zug- als auch Druckkräfte.

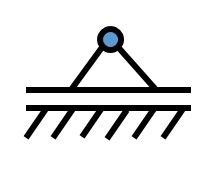
2-wertiges Lager

Bei einem 2-wertigen Lager ist der Freiheitsgrad weiter eingeschränkt Das 2-wertige Lager wirkt sowohl Kräften in x- als auch in y-Richtung entgegen. Es ist nur noch eine Drehbewegung um den Punkt P möglich.

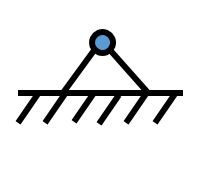
3-wertiges Lager

Der Kragbalken dient als Beispiel für ein 3-wertiges Lager. Der Balken ist in dem Punkt P fest eingemauert, er kann weder in x- noch in y-Richtung bewegt werden und auch ein Drehen um den Punkt P ist ausgeschlossen.

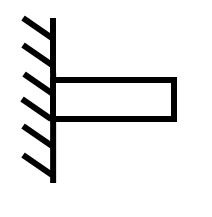
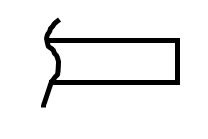
Rolle

Eine Rolle überträgt die Kräfte von einer Seite zur anderen im Verhältnis 1:1. Die Rolle ist in dem Punkt M so gelagert, dass sie in x- und y-Richtung gehalten wird, sich aber frei drehen kann, sie kann kein resultierendes Drehmoment aufnehmen. Beide Seilkräfte F_S1 und F_S2 greifen tangential an der Rolle an und erzeugen um den Punkt M ein Drehmoment,

M_S1 = F_S1 * r                                                        Drehrichtung links (positiv)

M_S2 = F_S2 * r                                                        Drehrichtung rechts (negativ)

Da sich die Rolle im statischen Zustand nicht dreht, muss das resultierende Drehmoment gleich Null sein

+ M_S1 – M_S2 = 0

Damit müssen die beiden Beträge der Drehmomente gleich groß sein und damit auch die beiden Beträge der Kräfte F_S1 und F_S2. Die beiden Kräfte F_Mx und F_My ergeben sich auf gleiche Weise:

+ F_My – F_S1 – F_S2y = 0

+ F_S2x – F_Mx = 0

Aufgrund dieser Überlegungen war die Annahme F_S1 = F_S2 bei der Untersuchung der Leuchte richtig. In der Animation kann in der rechten Abbildung der Punkt P bewegt werden.