Kraft und Drehmoment
Kraft
Die zentrale physikalische Größe in der Statik ist die Kraft. Auf die zu untersuchenden Bauteile wirken von außen belastenden Kräfte, das kann z.B. die Gewichtskraft eines Autos sein, das über die Brücke fährt, aber auch das Eigengewicht des Bauteils selbst oder eine angreifende Windlast auf ein Hochhaus. Nach dem zweiten Newton’schen Gesetz gilt für Kräfte:
\(F=m \cdot a\) (vektorielle Kraft = Masse \(\cdot\) vektorielle Beschleunigung)
Die Einheiten dieser Größen sind Newton \(N\) für die Kraft \(F\), Kilogramm \(kg\) für die Masse \(m\) und Meter pro Quadratsekunde \((\frac {m}{s^2})\) für die Beschleunigung \(a\). \(1 N\) entspricht somit \(1\frac {kg \cdot m}{s^2}\).
Als vektorielle Größe hat die Kraft \(F\) drei Eigenschaften:
– einen Angriffspunkt
– eine Richtung und
– einen Betrag.
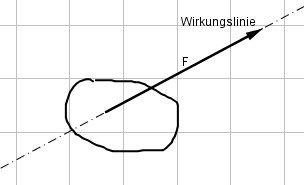
Die Kraft setzt an einem Punkt P an und wirkt in eine Richtung mit einem bestimmten Betrag. Sie kann somit gut als Vektor sichtbar gemacht werden. Verlängert man den Vektor in beide Richtungen, so erhält man die Wirkungslinie der Kraft. In der Physik werden Vektoren mit einem Pfeil über dem Formelzeichen gekennzeichnet.
In vielen Lehrbüchern der Statik wird dieser Pfeil weggelassen, so auch in diesem Lernbereich, wissend, dass Kräfte Vektoren sind!
Für die Gewichtskraft ergibt sich damit
\(F_G = m \cdot g\) mit \(g\) als Ortsfaktor
Die Gewichtskraft setzt immer im Schwerpunkt eines Körpers an.
Der Wert für g beträgt \(g = 9,81 \frac {m}{s^2}\), es wird in der Statik aber auch häufig gerundet mit \(g = 10 \frac {m}{s^2}\) gerechnet. Der dadurch auftretende Fehler vergrößert die geometrische Größe der zu berechnenden Bauteile, d.h. die Sicherheit ist gewährleistet.
Drehmoment

Um die Lampe am Seil mit der Winde hochzuziehen, wird eine Kraft benötig. Die Kraft wird dabei in eine Dreh’Kraft‘ umgesetzt, in ein Drehmoment. Aus der Erfahrung ist bekannt, dass das auf die Kurbel wirkende Drehmoment umso größerist, je länger der Hebel ist und die Kraft mit dem Hebel 90° einschließen soll.
Unter einem Drehmoment versteht man das Produkt (mathematisch: Kreuzprodukt) aus einer Kraft F und dem senkrechten Abstand l ihrer Wirkungslinie vom Drehpunkt C. Der Dreh- oder Bezugspunkt wird als Index (Mehrzahl: Indizes) mit angegeben.
\(M_C = F \cdot l\) mit \(M_C\) als Drehmoment mit Bezugspunkt C
Da der Abstand \(l\) mit der Einheit Meter angegeben wird, ergibt sich die Einheit des
Drehmoments:\( [M] = 1Nm\).
Im Beispiel der Drehwinde können Sie den Radius der Kurbel (\(r\)), den Ausgangspunkt (\(A\)) der Kraft \(F\) und die Position der Kurbel verändern.
Drehen verschiedene Drehmomente um einen Punkt, so können sie addiert werden, die Drehrichtung bestimmt das Vorzeichen. Das Drehmoment hat ebenso wie die Kraft drei Eigenschaften:
– Drehachse
– Drehrichtung und
– Betrag.
Drehmomente werden mit einem Drehpfeil in das Kraftsystem eingezeichnet.
