Freischneiden

Ziel der Statik ist es, Bauteile zu dimensionieren. Dazu müssen die von außen angreifenden Kräfte (Lasten) und die entsprechenden Gegenkräfte bekannt sein. Die Gegenkräfte sind aber in verbauten Teilen meist nicht unmittelbar sichtbar, sie müssen also sichtbar gemacht werden. Dazu wird der Körper „freigeschnitten“. Dieses nach Leonhard Euler (1707 – 1783) benannte Schnittprinzip ermöglicht es, angreifende Kräfte (rot) und Gegenkräfte (grün) sichtbar zu machen. Am Beispiel des Seils (Kabel) und des Hakens H der Deckenleuchte soll dies veranschaulicht werden. Grundlage ist das 3. Axiom (Axiome).

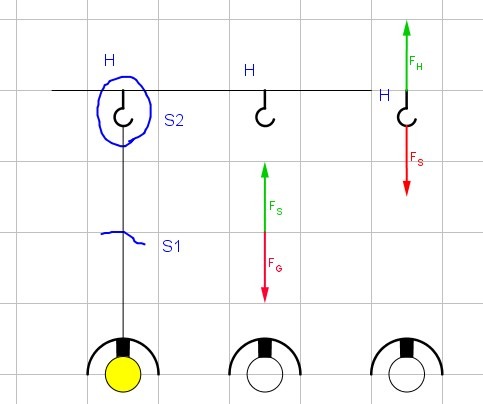
Wird in einem ersten Schritt das Kabel der Leuchte mit dem Schnitt S1 gedanklich freigeschnitten, so muss die Leuchte auch weiterhin im Gleichgewicht bleiben. Die angreifende Kraft F_G der Leuchte ruft eine Gegenkraft F_S im Seil hervor. Sind beide Kräfte gleich groß, befindet sich der Punkt (Körper) im Gleichgewicht. Ebenso kann mit jedem Punkt K (siehe nächste Aufgabe) des Seils verfahren werden.

F_S = F_G

Ebenso wird jetzt mit dem Haken verfahren. Der Schnittverlauf S2 umschließt den Haken. Als angreifende Kraft wirkt F_S und ruft die Gegenkraft F_H hervor, die den Haken in der Decke hält. Der Haken ist wiederum dann im Gleichgewicht, wenn die beiden Kräfte F_S und F_H gleich groß sind. 

F_H = F_S

Zusammengefasst ergibt sich, dass die Kraft im Haken gleich der Gewichtskraft ist.

F_H = F_G

Kurz gesagt: F_G zieht am Seil, das Seil zieht am Haken.

Dieses einfache Beispiel wird im Folgenden so verändert, dass die Leuchte nicht mehr direkt am Deckenhaken befestigt ist, sondern das Seil (Kabel) über Haken H geführt wird und erst an der Stelle P von einer Person mit der Kraft F_s1 gehalten wird.

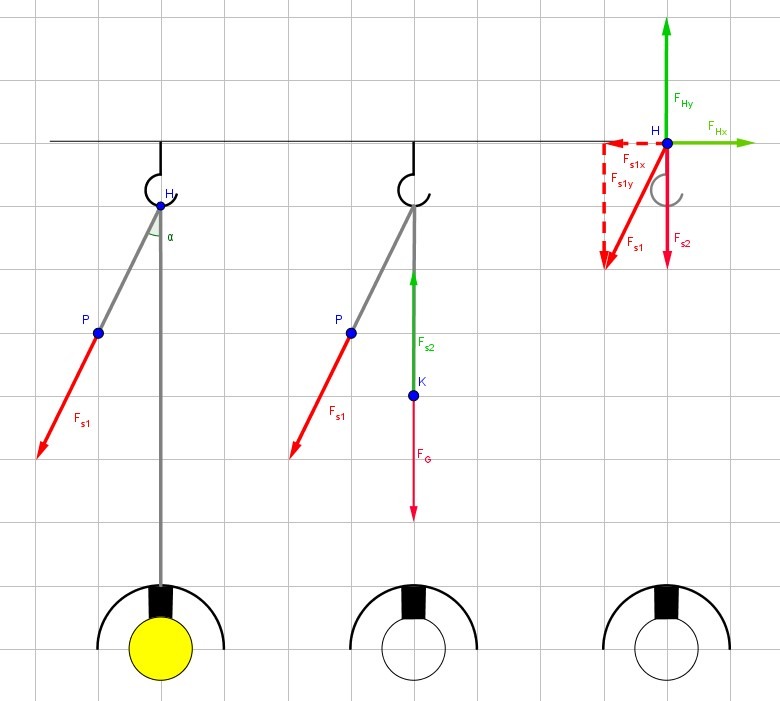
Durch das erste Freischneiden im Punkt K wird, wie schon oben erklärt, die Kraft im Seil F_S2 bestimmt. Auf den Haken H wirken jetzt die zwei Seilkräfte F_S1 und F_S2 (begründete Annahme F_S1 = F_S2, sonst bewegt sich die Leuchte auf- oder abwärts, siehe (Rolle). Der Haken wird in einen masselosen Punkt überführt, da seine Abmessungen klein sind gegenüber den Seillängen. Jetzt kann der Haken freigeschnitten werden. Es könnten nun zunächst die Gegenkräfte so eingezeichnet werden, dass sowohl für F_S1 und F_S2 eine Gegenkraft auf der gleichen Wirkungslinie in entgegengesetzter Richtung eingetragen wird. Diese beiden Gegenkräfte können nach dem 2. Axiom zusammengefasst werden. Da es für die Dimensionierung des Bauteils jedoch interessant ist, welche Normal– und Querkräfte wirken, können die Gegenkräfte auch gleich als F_Hx und F_Hy eingetragen werden.

Die beiden Seilkräfte müssen in ihre x- und y-Komponenten aufgeteilt werden und diese dann getrennt voneinander zu F_Hx und F_Hy addiert werden. In dem vorliegenden Beispiel ist die resultierende Kraft in y-Richtung F_Hy die Normalkraft, die in x-Richtung F_Hx die Schubkraft. Die resultierende Gesamtkraft ist von untergeordneter Bedeutung. Wird ausschließlich eine rechnerische Lösung erwartet, dann werden die Kräfte nur nach Angriffspunkt und Richtung eingetragen, der Betrag wird errechnet und muss bzw. kann nicht maßstabsgetreu gezeichnet werden.

Je nach Richtung der Kräfte zum beanspruchten Querschnitt wird zwischen Normalkräften (senkrecht zum Querschnitt) und Quer-, Schub- oder Scherkräften (im Querschnitt) unterschieden. Die maximal zulässigen Normal- und Querspannungen sind unterschiedlich groß.