Übung zur Kräftezerlegung an der schiefe Ebene

Im Folgenden finden Sie eine umfangreiches Applet zum Einüben von Kräfteplänen und beschleunigten Bewegungen an schiefen Ebenen.

Das Applet können Sie auch unter diesem Link in einem extra Fenster öffnen.

 

 

Übung zum Applet „Schiefe Ebene“:

Sie erkennen, dass sich anfangs nichts bewegt. Es herrscht also Kräftegleichgewicht und es existiert keine resultierende Kraft, die beschleunigend wirkt.

Aufgabe 1: Die resultierende Kraft

Ziehen Sie den gelben Punkt an der Ecke der geneigten Ebene, bis eine resultierende Kraft \(\vec{F}_{Res}\) (schwarzer Vektorpfeil) entsteht. Diese resultierende Kraft beschleunigt den Körper den Hang hinab. Beachten Sie dabei die Änderung des Namens der in rot dargestellten Reibungskraft, wir kommen später darauf zurück. Drücken Sie dann das Reset-Symbol rechts oben in der Ecke.

Aufgabe 2: Die elastische Kraft der Unterlage

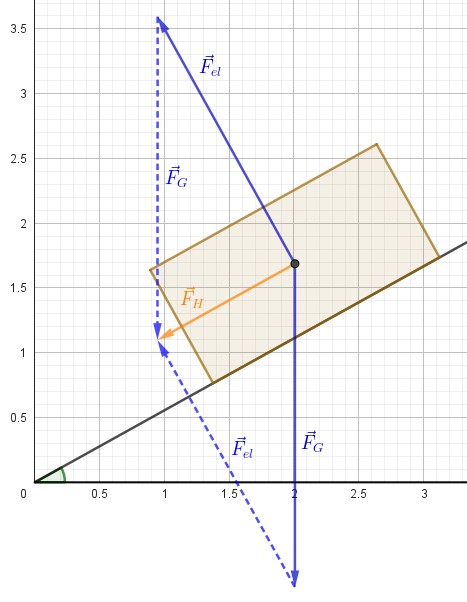
In blau sind die grundlegenden auf den Körper wirkenden Kräfte eingezeichnet: Die Gewichtskraft \(\vec{F}_G\) und die sogenannte „elastische“ Kraft \(\vec{F}_{el}\) der Unterlage. (Anmerkung: Als „elastisch“ bezeichnet man in der Physik alle Objekte, die sich nicht dauerhaft unter Krafteinwirkung verformen. Es soll damit ausgesagt werden, dass der Körper nicht in die Oberfläche einsinkt.) Die elastische Kraft \(\vec{F}_{el}\) der Unterlage kann nur senkrecht zur Oberfläche der Ebene wirken und steht deshalb der Gewichtskraft nicht direkt entgegen, sondern ist ebenfalls um den Neigungswinkel \(\alpha\) der schiefen Ebene geneigt.

Bewegen Sie wieder die geneigte Ebene und beobachten Sie dabei den (blauen) Kraftvektor \(\vec{F}_{el}\) genau. Die elastische Kraft der Unterlage steht stets senkrecht auf der Ebene und wird umso kleiner, je größer der Winkel \(\alpha\) wird. Maximal wird die Kraft der Unterlage auf den Körper nur bei einem Winkel von \(\alpha=0^\circ\), also einer waagrechten Ebene.

Aufgabe 3: Die Hangabtriebskraft

Aus der Gewichtskraft und der elastischen Kraft entsteht die Hangabtriebskraft:

\(\vec{F}_H = \vec{F}_G+\vec{F}_{el} \).     (Vorsicht: Vektoraddition!)

Bewegen Sie wieder die geneigte Ebene und verstehen Sie, wie der (orange) eingezeichnete Vektor der Hangabtriebskraft \(\vec{F}_H\) aus den beiden (blauen) Vektoren \( \vec{F}_G\) und \(\vec{F}_{el}\) entsteht. Es ist leicht einzusehen, dass die Hangabtriebskraft mit größerem Winkel \(\alpha\) zunimmt. Stellen Sie auch den extremen Winkel \(\alpha=90^\circ\) ein und erkennen Sie, dass die Hangabtriebskraft maximal den Wert der Gewichtskraft annehmen kann.

Vektoraddition \(\vec{F}_G+\vec{F}_{el} = \vec{F}_H \) veranschaulicht. Legt man die beiden (blauen) Vektoren der Gewichtskraft und elastischen Kraft der Unterlage aneinander, so erhält man immer den (orangenen) Vektor der Hangabtriebskraft:

Aufgabe 4: Die Normalkraft und die Reibungskraft

Die ebenfalls (orange) eingezeichnete Normalkraft ist die Gegenkraft zur elastischen Kraft: Genau so wie die Unterlage auf das Objekt drückt, drückt auch das Objekt auf die Unterlage. Diese Normalkraft ist die Ursache für die Reibungskraft. Es gilt mit der Reibungszahl \(\mu\) für den Betrag der Reibungskraft \(|\vec{F}_R|=\mu \cdot |\vec{F}_N|\). Im Prinzip kann die Reibungskraft also um so größer werden, je kleiner der Neigungswinkel der Ebene ist. Dies ist im Applet nicht so einfach zu sehen, da die Haftreibung niemals größer wird, als sie zum Festhalten des Objekts unbedingt sein muss.

Es gilt dabei immer, dass die Reibung einer möglichen Bewegung entgegen wirkt. Sie kann aber selbst keine Erhöhung der Geschwindigkeit bewirken, weswegen ein zu langer Kraftvektor für die Reibungskraft nicht sinnvoll ist (d.h. auch wenn sich rechnerisch eine höhere Reibungskraft ergibt, zeichnet man den Reibungskraftvektor nur so lange, dass er andere wirkende Kräfte wie Hangabtriebskraft oder Zugkraft ausgleicht).

Zudem unterscheidet man bei diesem Versuch zwischen Haftreibung \(\vec{F}_{R,Haft}\) und Gleitreibung \(\vec{F}_{R,Gleit}\): So lange sich das Objekt nicht bewegt, wirkt Haftreibung. Rutscht das Objekt auf der geneigten Ebene, so wirkt Gleitreibung. In der Realität ist die Gleitreibung normalerweise kleiner als die Haftreibung. (Da ein sprunghafter Wechsel bei der Größe der Reibungszahl beim schnellen Verändern des Winkels \(\alpha\) verwirrend sein kann wurde in diesem Applet darauf verzichtet.)

Drücken Sie das Reset-Symbol rechts oben in der Ecke. Ermitteln Sie durch Ausprobieren den (ungefähren) Neigungswinkel \(\alpha\) der Ebene, bei dem die Haftreibung nicht mehr ausreicht um den Körper festzuhalten.

Bei einer Reibungszahl von \(\mu=0{,}65\) reicht die Reibungskraft ab einem Neigungswinkel der Ebene von etwas über \(\alpha\approx 33^\circ\) nicht mehr aus, um den Körper an Ort und Stelle festzuhalten.

\( \)

Aufgabe 5: Schieben, Ziehen, Drücken

Zusätzlich können auf das auf der schiefen Ebene liegende Objekt noch weitere Kräfte ausgeübt werden, wenn es z.B. gezogen oder geschoben wird. Auch wenn es einen eigenen Antrieb besitzt (z.B. Motor) wirkt eine zusätzliche Kraft. Diese wird im Applet mit der (hellblau) eingezeichneten Kraft \(\vec{F}_{Zug}\) symbolisiert. Besonders bemerkenswert ist hier, dass die Reibungskraft nun sogar hangabwärts wirken kann, wenn man nur stark genug Richtung hangaufwärts zieht.

Drücken Sie das Reset-Symbol rechts oben in der Ecke. Variieren Sie die Zugkraft und beobachten Sie dabei den Vektor der Reibungskraft genau. Bestimmen Sie, ab ungefähr welchen Zugkraftbeträgen die Reibungskraft nicht mehr ausreicht, um den Körper festzuhalten und begründen Sie, warum dies so ist.

Zieht man zusätzlich nach links-unten („negative Zahlen“), so reicht schon ein Zugkraftbetrag von etwas über 0,2 N aus, damit das Objekt nicht mehr von der Haftreibungskraft gehalten werden kann. Dies kommt daher, weil Zugkraft und Hangabtriebskraft gemeinsam hangabwärts gegen die Reibungskraft wirken.

Zieht man zusätzlich nach rechts-oben („positive Zahlen“), so muss ein deutlich höherer Zugkraftbetrag von über 2,6 N eingestellt werden, damit das Objekt nicht mehr von der Haftreibung gehalten werden kann. Da die Reibungskraft immer entgegen einer möglichen Bewegung wirkt, wirkt diese in diesem Fall sogar mit der Hangabtriebskraft zusammen hangabwärts. Deshalb müssen nun mit der Zugkraft sowohl Hangabtriebskraft als auch Reibungskraft überwunden werden, um das Objekt in Bewegung zu versetzen.

\( \)

Aufgabe 6: Kräftebeträge berechnen

Drücken Sie das Reset-Symbol rechts oben in der Ecke. Setzen Sie den Haken beim Menüpunkt „Kräftebeträge“. Im Applet werden nun die Beträge der einzelnen Kräfte angezeigt. Verifizieren Sie diese durch Rechnung.

Bereits eingestellt: Gewichtskraft \(F_G=2{,}5\;N\)

Normalkraft (und elastische Kraft):

\( F_N =F_{el}= F_G \cdot \cos (\alpha) = 2{,}5\;N \cdot \cos (29{,}05^\circ) \approx 2{,}19\;N \)

Hangabtriebskraft:

\( F_H = F_G \cdot \sin (\alpha) = 2{,}5\;N \cdot \sin (29{,}05^\circ) \approx 1{,}21\;N \)

Maximale Reibungskraft:

\( F_R = \mu \cdot F_N = \mu \cdot F_G \cdot \cos (\alpha) = 0{,}65 \cdot 2{,}5\;N \cdot \cos (29{,}05^\circ) \approx 1{,}42\;N\)

\( \)

Aufgabe 7: Beschleunigte Bewegung an der schiefen Ebene

Setzen Sie den Haken beim Menüpunkt „Beträge der Bewegungskoordinaten“. Hier werden die Beschleunigung des Objekts, dessen momentane Geschwindigkeit und die von dem Objekt zurückgelegte Strecke zu jedem Zeitpunkt angezeigt. (Hinweis: Wenn Sie den Haken bei „Zeit an“ wegnehmen, kann der Zeitregler \(t\) auf jeden beliebigen Zeitpunkt eingestellt werden.)

Drücken Sie das Reset-Symbol rechts oben in der Ecke und stellen Sie die Zugkraft auf „Zugkraft = 3“ ein. Es entsteht eine zusätzlicher (hellblauer) Kraftvektor mit dem Betrag \(3{,}0\;N\). Das Objekt wird jetzt mit einer resultierenden Kraft \(\vec{F}_{Res}\) nach rechts-oben beschleunigt. Berechnen Sie den Betrag dieser resultierenden Kraft, den Betrag der daraus resultierenden Beschleunigung und ermitteln Sie, welche Zeit das Objekt für die ersten 2,0 Meter Strecke benötigt.

Es ist zu beachten, dass die Reibungszahl \(\mu=0{,}65\) entgegen früherer Aufgaben hier jetzt als Gleitreibungszahl verwendet wird.

Die beschleunigende resultierende Kraft erhält man aus einem Kraftansatz:

Vektoriell gilt \(\vec{F}_{Res}=\vec{F}_{Zug}+\vec{F}_H+\vec{F}_{R,Gleit}\)

Für die Beträge der Kräfte gilt allerdings

\({F}_{Res}={F}_{Zug}-{F}_H-{F}_{R,Gleit}\)

Die Werte kann man ausrechnen oder aus Aufgabe 6 entnehmen:

\({F}_{Res}=3\;N-1{,}21\;N-1{,}42\;N\approx 0{,}37\;N\)

Die resultierende Kraft beschleunigt das Objekt mit der Masse \(m=\frac{F_G}{g}=\frac{2{,}5\;N}{9{,}81\frac{N}{kg}}\approx 0{,}25\;kg\) mit

\(F_{Beschl}=m \cdot a\), d.h. \(a=\frac{F_{Res}}{m}=\frac{0{,}37\;N}{0{,}25\;kg}\approx 1{,}48\;\frac{m}{s^2}\)

Mit dieser Beschleunigung kann man die Zeit für 2,0 Meter zurückgelegte Strecke berechnen:

\(s(t)=\frac{1}{2} \cdot a \cdot t^2\), also \(t=\sqrt{\frac{2\cdot s}{a}} =\sqrt{\frac{2\cdot 2{,}0\;m}{1{,}48\;\frac{m}{s^2}}}\approx 1{,}6\;s\)

HINWEIS: Hier erkennt man, dass durch mehrere Rechenschritte Rundungsfehler entstehen:

Nimmt man die genaueren Werte aus dem Taschenrechner für \({F}_{Res}\approx 0{,}365499\;N\) und \(m \approx 0,254842\;kg\), so erhält man die im Applet angegebene Beschleunigung von \(a\approx 1{,}43\;\frac{m}{s^2}\). Damit steigt die Zeit für die zurückgelegte Strecke von 2,0 Metern leicht auf \(t\approx 1{,}67\;s\approx 1{,}7\;s\). Stellen Sie im Applet die Zeit auf „t = 1.67“ um dies zu verifizieren.

Weiter
Zurück