Newton’sche Gesetze: Aufgaben (Teil 1)

Aufgabe 1: Schlitten auf vereister Ebene

1.0 Ein Schlitten der Masse \( m= 65 \; \mathrm{kg} \) befindet sich auf ebener, vereister (reibungsfreier) Fläche im Stillstand. Ab dem Zeitpunkt \(  t_0 = 0  \) wird  mit einer Kraft vom Betrag \( 50 \; \mathrm{N} \) horizontal am Schlitten gezogen.

1.1 Ermitteln Sie den Betrag der Beschleunigung, die der Schlitten erfährt.

1.2 Berechnen Sie die zurückgelegte Strecke und den Geschwindigkeitsbetrag des Schlittens zum Zeitpunkt \(  t_1 = 3{,}0 \;  \mathrm{s} \)

\( a = \frac{F}{m}=\frac{50 \mathrm{N}}{65 \mathrm{kg}}= 0{,}77 \; \frac{\mathrm{m}}{\mathrm{s^2}} \)

\( s =\frac{1}{2} \cdot a \cdot t²= \frac{1}{2} \cdot 0{,}77 \; \frac{\mathrm{m}}{\mathrm{s^2}} \cdot (3{,}0 \; \mathrm{s})^2  = 3{,}5 \; \mathrm{m} \)

\(v=a \cdot t = 0{,}77 \; \frac{\mathrm{m}}{\mathrm{s²}} \cdot  3{,}0 \; \mathrm{s}= 2{,}3 \; \frac{\mathrm{m}}{\mathrm{s}} \)

Aufgabe 2: Fahrbahnwagen auf horizontaler Ebene

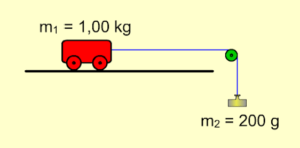2.0 Ein Fahrbahnwagen der Masse \( m_1 = 1{,}00 \; \mathrm{kg} \) steht reibungsfrei auf einer waagrechten Unterlage. Über einen Faden beschleunigt ihn ein Körper der Masse \( m_2 = 200 \; \mathrm{g} \)

2.1 Berechnen Sie den Betrag der Beschleunigung mit der sich die beiden Wagen bewegen.

2.2 Begründen Sie rechnerisch, ob die Fahrbahnwagen sich mit 10-facher Beschleunigung bewegen würden, wenn der Fahrbahnwagen 2 eine 10-fache Masse \( m_2 = 2{,}00 \; \mathrm{kg} \) hätte.

\(  F_{res} = F_{g_2}=m_2 \cdot g = 0{,}200 \; \mathrm{kg} \cdot 9{,}81 \; \frac{\mathrm{m}}{\mathrm{s²}} = 1{,}96 \; \mathrm{N} \)

\(  F_{res} = m_{ges} \cdot a \)

\(  a= \frac{ F_{res}}{m_{ges}} = \frac{ F_{res}}{m_1 + m_2} = \frac{ 1{,}96 \; \mathrm{N}}{1{,}00 \; \mathrm{kg} + 0{,}200 \; \mathrm{kg}} = 1{,}63 \; \frac{\mathrm{m}}{\mathrm{s² }} \)

\(  F_{res} = F_{g_2}=m_2 \cdot g = 2{,}00 \; \mathrm{kg} \cdot 9{,}81 \; \frac{\mathrm{m}}{\mathrm{s²}} = 19{,}6 \; \mathrm{N} \)

\(  F_{res} = m_{ges} \cdot a \)

\(  a= \frac{ F_{res}}{m_{ges}} = \frac{ F_{res}}{m_1 + m_2} = \frac{ 1{,}96 \; \mathrm{N}}{1{,}00 \; \mathrm{kg} + 2{,}00 \; \mathrm{kg}} = 6{,}53 \; \frac{\mathrm{m}}{\mathrm{s² }} \)

Trotz 10-facher Masse \( m_2 \) verzehntfacht sich die resultierende Beschleunigung nicht.

Aufgabe 3: Atwood'sche Fallmaschine


3.0 Zwei Massetsücke \( m_1 = 400 \; \mathrm{g} \)  und \( m_2 = 420 \; \mathrm{g} \), die über einen Faden verbunden sind, hängen über einer nahezu reibungsfrei gelagerten und masselosen Rolle.

3.1 Berechnen Sie den Betrag der Beschleunigung mit der sich beide Körper bewegen.

3.2 Ermitteln Sie wie groß die Masse \( m_2 \) sein müsste, damit die beiden Körper eine Beschleunigung vom Betrag \( a = 0{,}500 \; \frac{\mathrm{m}}{\mathrm{s²}} \) erfahren.

\(  F_{res} = F_{g_2} – F_{g_1}=m_2 \cdot g  – m_1 \cdot g = 0{,}420 \; \mathrm{kg} \cdot 9{,}81 \; \frac{\mathrm{m}}{\mathrm{s²}} – 0{,}400 \; \mathrm{kg} \cdot 9{,}81 \; \frac{\mathrm{m}}{\mathrm{s²}} =0{,}196 \; \mathrm{N} \)

\(  F_{res} = m_{ges} \cdot a \)

\(  a= \frac{ F_{res}}{m_{ges}} = \frac{ F_{res}}{m_1 + m_2} = \frac{ 0{,}196 \mathrm{N}}{0{,}400 \mathrm{kg} + 0{,}420 \mathrm{kg}} = 0{,}239 \; \frac{\mathrm{m}}{\mathrm{s² }} \)

\(  F_{res} = F_{g_2} – F_{g_1}=m_2 \cdot g – m_1 \cdot g = (m_2 – m_1) \cdot g = m_{ges} \cdot a = (m_1 + m_2) \cdot a \)

\(       (m_2 – m_1) \cdot g =     (m_1 + m_2) \cdot a        \)

\( m_2 \cdot g – m_1 \cdot g = m_1 \cdot a + m_2 \cdot a \)

\( m_2 \cdot g – m_2 \cdot a = m_1 \cdot a + m_1 \cdot g \)

\( m_2 \cdot (g-a) = m_1 \cdot (a+g) \)

\( m_2 = m_1 \cdot \frac{a+g}{g-a} = 400 \; \mathrm{g} \cdot \frac{0{,}500 \; \frac{\mathrm{m}}{\mathrm{s^2}} + 9{,}81 \frac{\mathrm{m}}{\mathrm{s^2} }}{9{,}81 \; \frac{\mathrm{m}}{\mathrm{s^2}}     –  0{,}500 \; \frac{\mathrm{m}}{\mathrm{s²}}} = 443 \; \mathrm{g} \)

Aufgabe 4: Aufzug

4.0 Eine Aufzugskabine mit der Masse \( 1,0 \mathrm{t} \) wird aus der Ruhe auf einem Weg von \( 2,5 \mathrm{m} \) konstant auf eine Geschwindigkeit vom Betrag \( 4,0 \frac{\mathrm{m}}{\mathrm{s}}  \) beschleunigt.

4.1 Ermitteln Sie den Betrag die Antriebskraft, die der Motor der Aufzugs aufbringen muss, wenn sich der Aufzug nach oben bewegt.

4.2 Berechnen Sie den Betrag dieser Antriebskraft, wenn sich der Aufzug nach unten bewegt.

Berechnung des Beschleunigungsbetrags:

\( v² = 2a \cdot \Delta x \)

\( a = \frac{v²}{2 \cdot \Delta x } = \frac{(4,0 \frac{\mathrm{m}}{\mathrm{s}})²}{2 \cdot 2,5 \mathrm{m}} = 3,2 \frac{\mathrm{m}}{\mathrm{s^2}}\)

Berechnung des Betrages der resultierenden (beschleunigenden) Kraft:

\( F_{res}= m \cdot a = 1,0 \cdot 10³ \mathrm{kg} \cdot 3,2 \frac{\mathrm{m}}{\mathrm{s²}}= 3,2 \cdot 10³ \mathrm{N}\)

Die resultierende Kraft ergibt sich bei einer Fahrt nach oben aus:

\( F_{res} = F_{Antrieb} – F_{g} \)

Es folgt also:

\( F_{Antrieb} = F_{res} + F_{g} = F_{res} + m \cdot g = 3,2 \cdot 10³ \mathrm{N} + 1,0 \cdot 10³ \mathrm{t} \cdot 9,81 \frac{\mathrm{m}}{\mathrm{s² }} = 13 \mathrm{kN} \)

\( a =  3,2 \frac{\mathrm{m}}{\mathrm{s^2}}\) (vgl. 4.1)

\( F_{res}= 3,2 \cdot 10³ \mathrm{N}\) (vgl. 4.1)

Die resultierende Kraft ergibt sich bei einer Fahrt nach unten aus:

\( F_{res} = F_{g} + F_{Antrieb} \)

Es folgt also:

\( F_{Antrieb} = F_{res} – F_{g} = F_{res} – m \cdot g = 3,2 \cdot 10³ \mathrm{N} – 1,0 \cdot 10³ \mathrm{t} \cdot 9,81 \frac{\mathrm{m}}{\mathrm{s² }} = -6,6 \mathrm{kN} \)

Bei einer Fahrt nach unten muss der Aufzug also mit einer Kraft vom Betrag \( 6,6 \mathrm{kN} \) bremsen.

Aufgabe 5: Fahrbahnexperiment

Ein Fahrbahnwagen der Masse \( m_W \) wird von einem kleinen Gewicht der Masse \( m_G  = 2,00 \mathrm{g}\) beschleunigt. Zum Zeitpunkt \( t_0=0 \) wird er am Ort \( x_0=0\) losgelassen. Am Ort \( x_1=0,170 \mathrm{m}\) befindet sich eine erste Lichtschranke, die einen Kurzzeitmesser startet. Passiert der Fahrbahnwagen am Ort \( x_2=1,07 \mathrm{m}\) die zweite Lichtschranke, stoppt der Kurzzeitmesser. Die gemessene Zeitspanne \( \Delta t\) beträgt \( 2,47 \mathrm{s} \).

Berechnen Sie den Betrag \( a \) der Beschleunigung  des Wagens sowie seine Masse \( m_W \).

Berechnung des Beschleunigungsbetrags:

Da \( x_0=0 \) und \( v_{0_x} =0 \) (Start aus der Ruhe), gilt die Bewegungsgleichung \( x_(t)=\frac{1}{2} \cdot a_x \cdot t² \)

Folglich gelten für \( x_1 \) bzw. \( x_2 \): \(x_1= x_(t_1)=\frac{1}{2} \cdot a_x \cdot {t_1}^2 \) bzw. \(x_2= x_(t_2)=\frac{1}{2} \cdot a_x \cdot {t_2}^2 \)

Daraus folgt: \( t_1 = \sqrt{\frac{2 x_1}{a_x} } \) bzw. \( t_2 = \sqrt{\frac{2 x_2}{a_x} } \)

Mit \( t_2 – t_1 = \Delta t\) erhält man:

\( \Delta t = \sqrt{\frac{2 x_2}{a_x}} – \sqrt{\frac{2 x_1}{a_x} } =   \frac{   \sqrt{2x_2} – \sqrt{2x_1} }{ \sqrt{a_x}  } \)

\( a_x = {( \frac{\sqrt{2x_2} – \sqrt{2x_1}}{\Delta t}         )}²  = {( \frac{\sqrt{2\cdot 1,07 \mathrm{m}} – \sqrt{2\cdot 0,170 \mathrm{m}}}{2,47 \mathrm{s}}         )}² = 0,127 \frac{\mathrm{m}}{\mathrm{s²}} \)

Berechnung der Masse \( m_W \):

\( F_{res}= m_G \cdot g = (m_W+m_G) \cdot a_x = m_W \cdot a_x + m_G \cdot a_x\)

\( m_G \cdot g – m_G \cdot a_x = m_W \cdot a_x \)

\( m_W = \frac{ m_G \cdot g – m_G \cdot a_x }{a_x} = m_g \cdot \frac{g}{a_x}- m_g= m_g \cdot (\frac{g}{a_x}- 1) = 2,00  \mathrm{g} \cdot (\frac{9,81}{0,127 \frac{\mathrm{m}}{\mathrm{s²}}} – 1) = 153 \mathrm{g} \)

Aufgabe 6: Zuordnung zu Newtonschen Axiomen

Weiter
Zurück