Impulsdiagramme: Zweidimensionaler Stoß

Beschreibung

In der Realität sind zentrale Stöße eher die Ausnahme. Normalerweise treffen die Schwerpunkte zweier Objekte versetzt aufeinander, so dass nach dem Stoß ein Winkel zwischen den Geschwindigkeitsvektoren entsteht. Dies ist oft gewollt, beispielsweise beim Billard, beim Eisstockschießen oder bei einem Kopfball im Fußball. Hier zeigt sich der Vorteil von Impulsdiagrammen mit Vektoren: Eine einfache Rechnung ist hier nicht mehr möglich, durch eine maßstabsgetreue Zeichnung sind aber schnell Aussagen über Richtungen und Beträge der Geschwindigkeiten nach dem Stoß getroffen.

Im folgenden Applet wird der vollständig elastische Stoß einer sich bewegenden blauen Kugel auf eine ruhende rote Kugel dargestellt (Rotationseffekte werden nicht mitberechnet). Dabei wird für jede Einstellung das passende Impulsdiagramm angezeigt. Der Gesamtimpuls vor dem Stoß besteht natürlich ausschließlich aus dem Impuls der sich bewegenden blauen Kugel. Der Impuls der ruhenden roten Kugel ist vor dem Stoß \(\vec{p}_{2,vorher}=\vec{0}\).

Nach dem Stoß teilt sich der Gesamtimpuls je nach Massen und Auftreffwinkel auf die beiden Kugeln auf. Durch den Versatz \(\Delta y\) kann man zwischen einem zentralen Stoß und einem streifenden Einfall wählen. Da im LehrplanPlus stets nach der Analyse von Stroboskopbildern gefragt ist, kann man mit dem Regler „Schrittweite“ den zeitlichen Abstand einzelner Positionen beim Stoßvorgangs einstellen und diese mit dem Haken bei „Spur Ein/Aus“ aufzeichnen.

Anfänglich sind die Massen im Applet identisch auf 1,5 kg eingestellt. Hier wird sofort eine Besonderheit deutlich: Bei gleichen Massen der beiden Stoßpartner entsteht im Impulsdiagramm immer ein rechter Winkel.

Um den Hintergrund zu verstehen, ist eine Betrachtung der  kinetischen Energien notwendig. Diese werden eigentlich erst im nächsten Kapitel betrachtet:

Bei diesem vollständig elastischen Stoß gilt neben der (vektoriellen) Impuls- auch die (skalare) Energieerhaltung:

Impuls: \(m_1  \vec{v}_1 = m_1  \vec{u}_1 + m_2  \vec{u}_2\)

Energie: \(\frac{1}{2} m_1  v_1^2 = \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2  u_2^2\)

Sind die Massen gleich, so wird aus dem Energieerhaltungssatz:

\(\frac{1}{2} m v_1^2 = \frac{1}{2} m u_1^2 + \frac{1}{2} m u_2^2\) \(\;\; |:\frac{1}{2} \;\; |: m\)

Teilt man durch die Masse \(m\) und den Faktor \(\frac{1}{2}\), so bleibt

\(v_1^2 = u_1^2 + u_2^2\) übrig.

Dies ist der Satz des Pythagoras, der ausschließlich in einem rechtwinkligen Dreieck gilt.

Dies bedeutet, dass bei einem solchen elastischen Stoß mit gleichen Massen immer ein rechtwinkliges Dreieck im Impulsdiagramm entstehen muss.

Geogebra Applet

Verwenden Sie entweder den Haken bei „Animation Ein/Aus“ oder ziehen Sie den Punkt auf der Zeitleiste, um den Stoßvorgang ablaufen zu lassen.

Das Applet kann unter diesem Link hier auf einer eigenen Seite aufgerufen werden.

 

 

Übungen zum Applet

  1. Laden Sie das Applet neu. Drücken Sie auf den Knopf „Animation Ein/Aus“ und beobachten Sie den nichtzentralen Stoß. Achten Sie auf den Impulspfeil der blauen Kugel vor und nach dem Stoß und vergleichen Sie diese mit dem Impulsdiagramm. Die beiden Impulse nach dem Stoß ergeben gemeinsam den Impuls der blauen Kugel vor dem Stoß: Der Impuls bleibt vor und nach dem Stoß erhalten. Da die Stoßpartner gleiche Massen besitzen, bildet das Impulsdiagramm ein rechtwinkliges Dreieck.
  2. Drücken Sie auf den Knopf „Spur Ein/Aus“ um die Stroboskopaufnahme aufzuzeichnen. Die Positionen der Kugeln werden in der Grundeinstellung alle \( \Delta t=0,1\;s\) als Punkte eingezeichnet. Die Geschwindigkeitsänderung der blauen Kugel wird deutlich, da die Punkte nach dem Stoß näher beieinander liegen. Zählen Sie die blauen Punkte vom Start x = 0 bis zur Stelle x = 6: Es liegen 10 Abstände von \( \Delta t=0,1\;s\) dazwischen, es ist also genau 1 Sekunde vergangen. Die Kugel hat also in 1 Sekunde die Entfernung von 6 Längeneinheiten (z.B. Meter) zurückgelegt: \(v_1=\frac{6\;m}{1\;s}=6\frac{m}{s}\). Mit einem Lineal könnte man nun also die Geschwindigkeiten der beiden Kugeln nach dem Stoß ermitteln.
  3. Drücken Sie auf „Reset“ um die Punkte zu löschen. Stellen Sie die „Schrittweite“ auf 0.2, setzen Sie den Haken bei „Spur Ein/Aus“ und lassen Sie die Animation laufen. Bei gleicher Geschwindigkeit sind also nun halb so viele Abstände vom Start x = 0 bis zur Stelle x = 6 erkennbar.
  4. Drücken Sie auf „Reset“ um die Punkte zu löschen. Ziehen Sie den Regler „Versatz \(\Delta y\)“ auf verschiedene Positionen und lassen Sie die Animation laufen. Beachten Sie, dass der 90°-Winkel bei gleichen Massen stets erhalten bleibt. Testen Sie auch die extremen Werte \(\Delta y=0\) und \(\Delta y=4\).
  5. Laden Sie das Applet neu, um alle Werte auf den Urzustand zu versetzen. Stellen Sie die Masse des blauen Körpers 1 auf 0,5 kg und lassen Sie die Animation laufen. Sie erkennen, dass die leichte Kugel sogar teilweise reflektiert wird und sich wieder etwas rückwärts bewegt. Verändern Sie den Versatz und beobachten Sie dabei die Veränderungen im Impulsdiagramm. Anmerkung: Der Impuls der blauen Kugel 1 nach dem Stoß \(\vec{p}_{u1}\) kann je nach Versatz jede erdenkliche Richtung annehmen.
  6. Laden Sie das Applet neu, um alle Werte auf den Urzustand zu versetzen. Stellen Sie die Masse des blauen Körpers 1 auf 3 kg und lassen Sie die Animation laufen. Sie erkennen, dass die schwere Kugel nicht zurückreflektiert wird und sich weiterhin nach rechts bewegt. Verändern Sie den Versatz und beobachten Sie dabei die Veränderungen im Impulsdiagramm. Anmerkung: Der Impuls der blauen Kugel 1 nach dem Stoß \(\vec{p}_{u1}\) kann je nach Versatz nur noch eine maximale Ablenkung von der ursprünglichen Bewegungsrichtung einnehmen (genauer: 30° Ablenkung bei \(\Delta y=2\)).
  7. Stellen Sie nun eigene Massen, Geschwindigkeiten und Versätze ein und lassen Sie auch die Positionen der Kugeln in verschiedenen Schrittweiten aufzeichnen, um das Stroboskopbild zu analysieren.

Beispiel: Zweidimensionaler Stoß

Stöße, bei denen sich mindestens einer der beiden Stoßpartner permanent verformt und/oder bei denen Bewegungsenergie in Wärme übergeht, heißen teilelastisch bzw. unelastisch. Beim zweidimensionalen Stoß gelten allerdings andere Bedingungen als beim eindimensionalen: Auch beim vollkommen unelastischen Stoß können sich hier die Stoßpartner wieder getrennt weiterbewegen, da es mehr Bewegungsrichtungen gibt als die Stoßrichtung. Verhaken sich die Stoßpartner ineinander und bewegen sich nach dem Stoß gemeinsam weiter, so wird sogar noch mehr Bewegungsenergie in Verformung und Wärme umgewandelt, als durch den (unelastischen) Stoß alleine. Beispielsweise bei Verkehrsunfällen kann man (leider) nahezu alle Formen von Stößen beobachten.

Im folgenden Beispiel soll ein einfacher zweidimensionaler Stoß betrachtet werden:

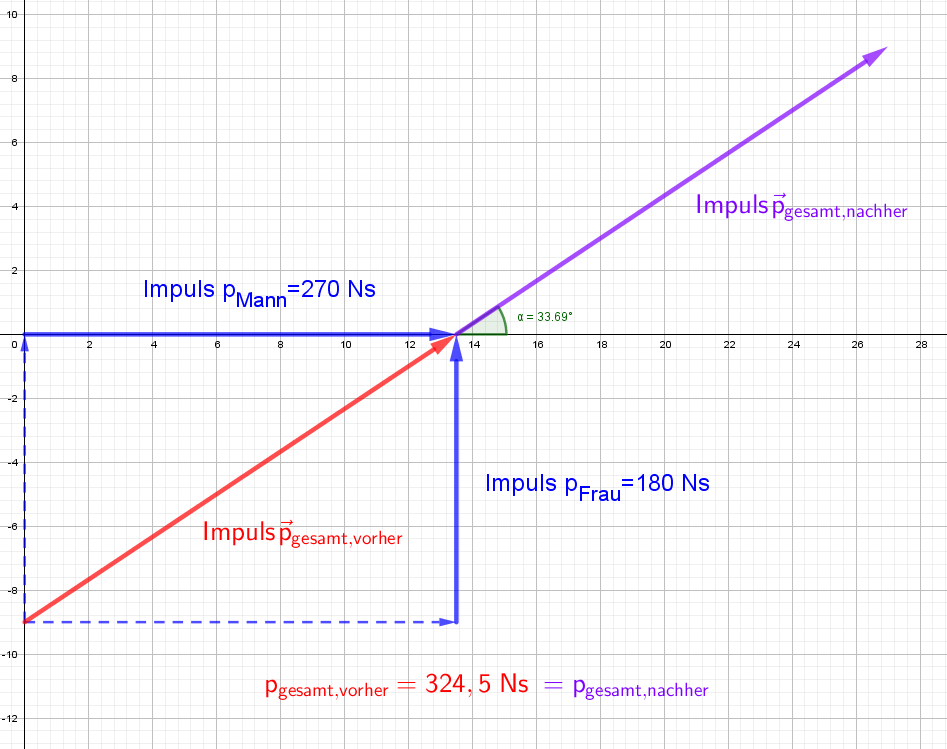
Aufgabe: Auf einer Eisbahn fährt ein Mann der Masse \(m_{Mann}=90\;kg\) und eine Frau der Masse \(m_{Frau}=60\;kg\) Schlittschuh. Beide sind mit dem Geschwindigkeitsbetrag \(v=3,0\frac{m}{s}\) unterwegs, allerdings stehen ihre sich kreuzenden Fahrtwege genau senkrecht aufeinander. Beim Aufeinandertreffen erschrecken die beiden Schlittschuhläufer und halten sich aneinander fest.

Bestimmen Sie die Richtung und den Betrag der gemeinsamen Geschwindigkeit nach dem Stoß mithilfe eines Impulsdiagramms. (Zusatz: Berechnen Sie die kinetischen Energien vor und nach dem Stoß und ermitteln Sie, wie viel Energie in Verformung bzw. Wärme übergegangen sein muss, damit sich die beiden gemeinsam weiterbewegen konnten.)

Lösung: Zuerst müssen die Einzelimpulse der beiden Stoßpartner berechnet und als Länge eines Vektors interpretiert werden. Anschließend kann man den Gesamtimpuls der beiden Schlittschuhläufer ermitteln. Da der Impuls auch nach dem Stoß erhalten bleibt, ist der ermittelte Gesamtimpuls dann auch der gemeinsame Impuls der beiden Läufer nach dem Stoß:

\(\vec{p}_{Mann}+\vec{p}_{Frau}=\vec{p}_{gesamt, vorher}=\vec{p}_{gesamt, nachher}\)

Für die Beträge gilt: \(p_{Mann}=90\;kg \cdot 3,0\frac{m}{s}=270\;Ns\) und \(p_{Frau}=60\;kg \cdot 3,0\frac{m}{s}=180\;Ns\).

Als Maßstab für das Impulsdiagramm wird \(1\;cm \; \widehat{=} \; 20\;Ns\) verwendet:

In diesem besonderen Fall kann der Gesamtimpuls mithilfe des Pythagoras berechnet werden.

Normalerweise misst man die Länge des Gesamtimpulses, in diesem Fall erhält man ca. 16,2 cm Länge. Dies entspricht einem Gesamtimpuls von

\(p_{gesamt,vorher}=p_{gesamt,nachher}\approx 324\;Ns\).

Für den Impuls gilt \(p=m \cdot v\). Sie bewegen sich nach dem Stoß also mit dem gemeinsamen Geschwindigkeitsbetrag \(u=\frac{p_{gesamt,nachher}}{m_{Mann}+m_{Frau}}=\frac{324\;Ns}{150\;kg}\approx 2,2\frac{m}{s}\) weiter. Die gemeinsame Richtung liegt ca. 34° zur Bewegungsrichtung des Mannes vor dem Stoß.

Zusatz:

Energien vorher: \(E_{kin,Mann}=\frac{1}{2}m v^2=\frac{1}{2}90\;kg \cdot (3\frac{m}{s})^2=405\;J\) und \(E_{kin,Frau}=\frac{1}{2}60\;kg \cdot (3\frac{m}{s})^2=270\;J\)

Energie nachher: \(E_{kin,gemeinsam}=\frac{1}{2}150 \cdot (2,2\frac{m}{s})^2=363\;J\)

Die in Verformung und Wärme übergegangene Energie beträgt also \(\Delta E=405\;J+270\;J-363\;J=312\;J\)

Geogebra Applet: Allgemeine zweidimensionalen Stöße

In einem sehr umfangreichen Geogebra-Applet können alle Stoßarten (elastisch, teilelastisch, unelastisch, sich verhakende Stoßpartner) eingestellt werden. Es lassen sich auch Größe, Masse, Bewegungsrichtungen und Geschwindigkeiten der Stoßpartner verändern. Nur Rotationen und tatsächliche Bewegungsänderungen durch Verformungen der Stoßpartner werden hingegen nicht beachtet. Der Umfang geht weit über das Verlangte im Physik-Fachabitur hinaus, trotzdem ist ein Spielen mit dem Applet sehr lehrreich, wenn man Stöße verstehen möchte. Verwenden Sie entweder den Haken bei „Animation Start/Stop“ oder ziehen Sie den Punkt auf der Zeitleiste t, um den Stoßvorgang ablaufen zu lassen.

Besonders eindrücklich wird hier der Umstand verständlich, dass der Gesamtimpuls vor dem Stoß und der Gesamtimpuls nach dem Stoß identisch sind (violetter Vektor). Zusätzlich werden die Impulsbeträge und die kinetischen Energien der beiden Stoßpartner vor und nach dem Stoß angegeben.

Die Stoßzahl gibt die Art des Stoßes an. Während die Stoßzahl 1 einen vollkommen elastischen Stoß beschreibt, bedeutet eine Stoßzahl von 0 einen vollkommen inelastischen Stoß. Bei 1 bleibt die Energie vollständig in der Bewegung der Stoßpartner erhalten, bei 0 geht maximal viel Energie in Verformungsarbeit (und letztlich Wärme) über. Die hier angegebenen Werte sollen einen ungefähren Eindruck vermitteln, was verschiedene Stoßzahlen bedeuten. Sie können als extrem ungenau angenommen werden, da sie je nach Ablauf des Stoßes stark variieren. Hier soll nur die Idee der unterschiedlichen Stoßarten vermittelt werden:

Stoßzahl Art des Stoßes Beispiel
1 Vollkommen elastisch Stöße auf atomarer Skala
ca. 0,95 Teilelastisch Billardkugeln aneinander
ca. 0,85 Teilelastisch Tennisball auf Schläger
ca. 0,70 Teilelastisch Zwei Autoscooter
ca. 0,40 Teilelastisch Squash-Ball auf Schläger
0,10 – 0,30 Teilelastisch Leichter Auffahrunfall (Stoßstange – Stoßstange)
0 Vollkommen unelastisch Schwerer Auffahrunfall
„Verkeilen/Verhaken/Kleben“ Schwerer Unfall, Schneeball auf Jacke

\( \)

Das Applet kann unter diesem Link hier auf einer eigenen Seite aufgerufen werden.

Weiter
Zurück