Weg und Zeit
Bei einer langen monotonen Autobahnfahrt mit der Geschwindigkeit \( v=120\frac{km}{h} \) beobachten Sie die Kilometerschilder am Rand der Fahrbahn. Alle 500 m sehen Sie auf blauen Metallschildern Zahlen wie 103,0; 103,5; 104,0 usw.. Von einem Schild zum nächsten benötigen Sie eine Zeitspanne von genau 15 Sekunden (Nachrechnen! Lösung unten). Sind die Zeitspannen zwischen diesen Markierungen stets gleich groß, so bezeichnet man die Fahrt als gleichförmig.
Versuch: Gleichförmige, geradlinige Bewegungen
Meist soll eine Abhängigkeit zwischen zwei Größen untersucht werden, im folgenden Video der Weg in Abhängigkeit von der Zeit. Andere Abhängigkeiten wären z.B. der Strom von der Spannung oder das Volumen von der Temperatur. Die Messwerte werden deshalb in einer Tabelle erfasst. Anschließend werden die Messwerte in einem sinnvoll gewählten Diagramm dargestellt. Aus diesen Diagrammen lassen sich relativ einfach bestehende Zusammenhänge der einzelnen Größen untereinander erkennen. Verbindet man die Messwerte und es ergibt sich z.B. eine Gerade, so sind die beiden Messgrößen proportional zueinander (Vergleiche: Steigung von Geraden in der Mathematik).
Die drei physikalischen Größen Weg (Formelzeichen \(s\), Einheit Meter \(m\)), Zeit (Formelzeichen \(t\), Einheit Sekunde \(s\)) und Geschwindigkeit (Formelzeichen \(v\), SI-Einheit Meter pro Sekunde \(\frac{m}{s}\)) sind aus dem täglichen Leben vertraut. Schauen Sie sich das folgende Video an und überlegen Sie sich, welche Schwierigkeiten und Fehler bei diesen Versuchen aufgetreten sind oder sein könnten.
Versuch: Auswertung
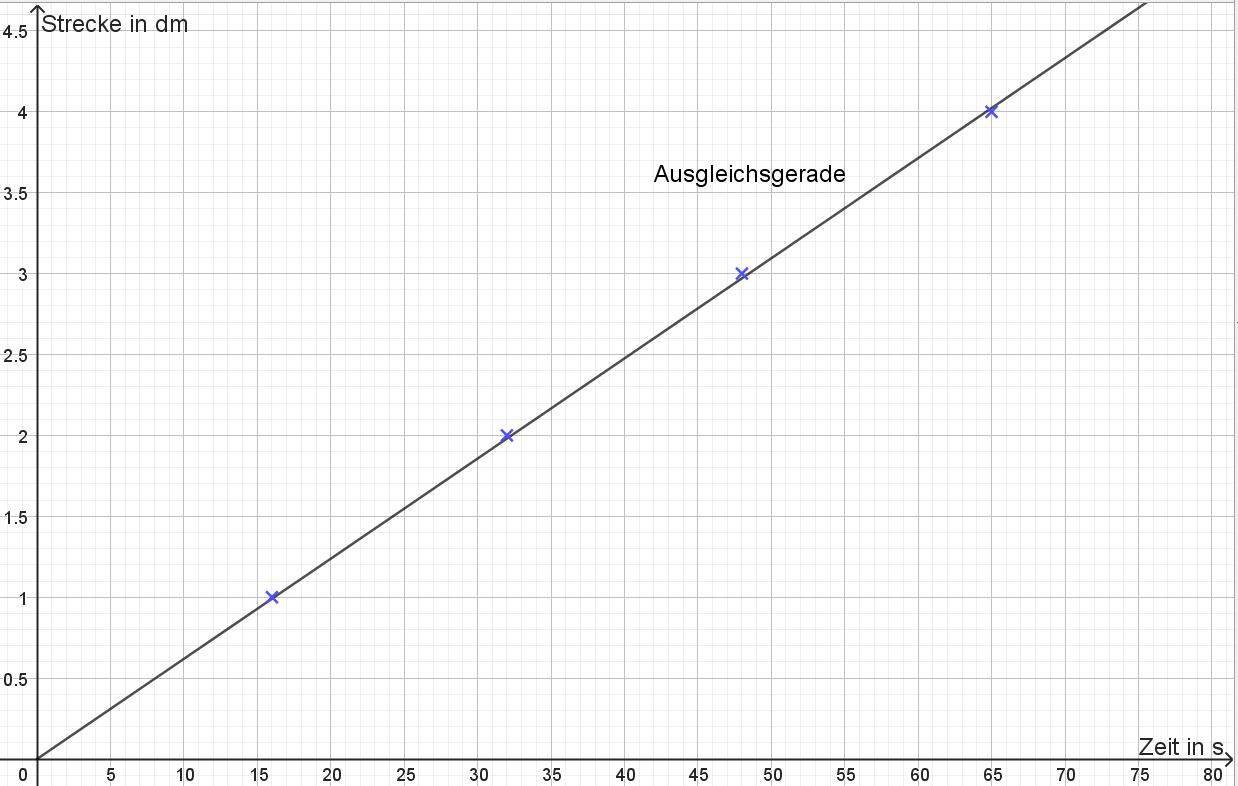
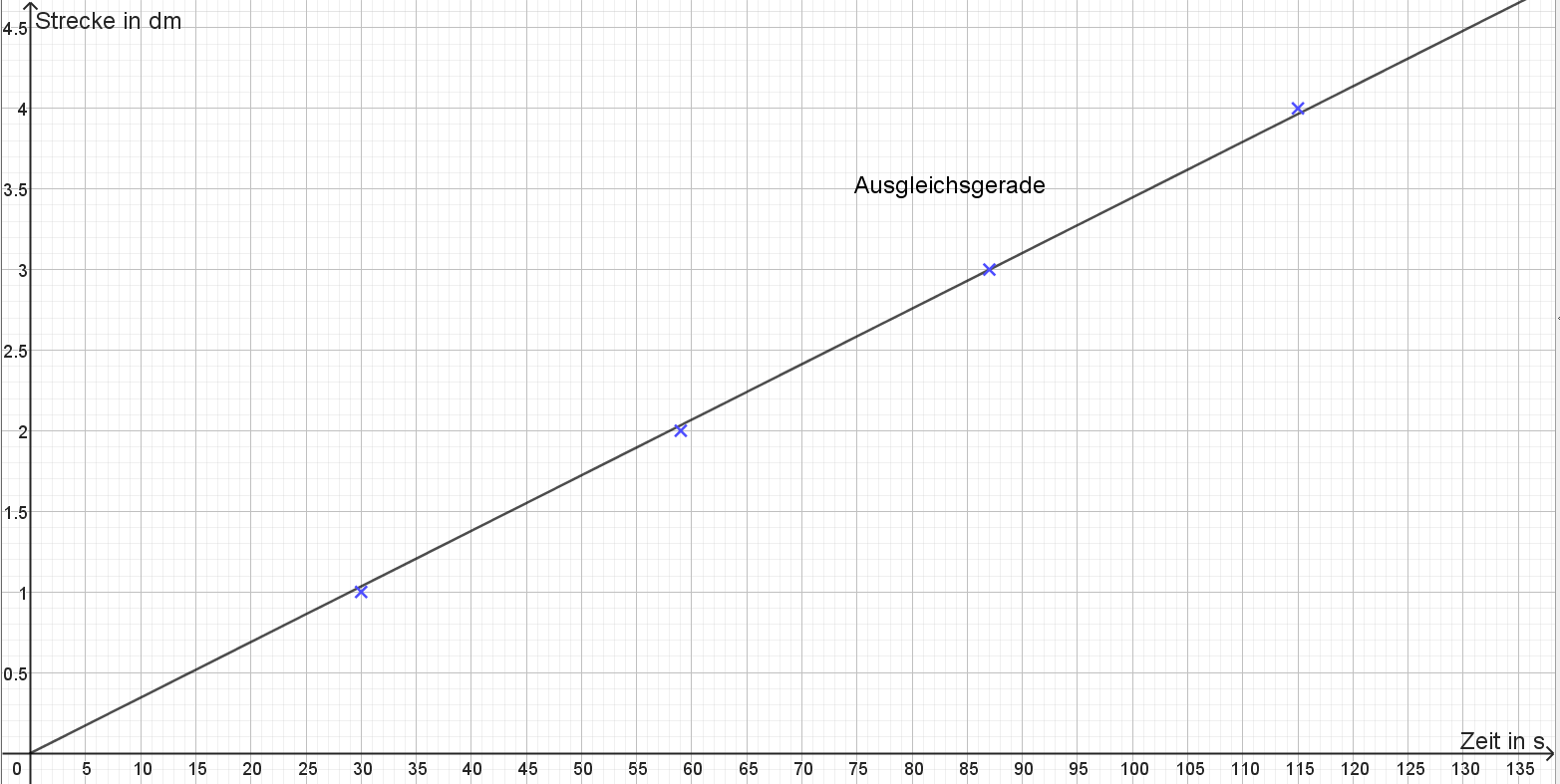
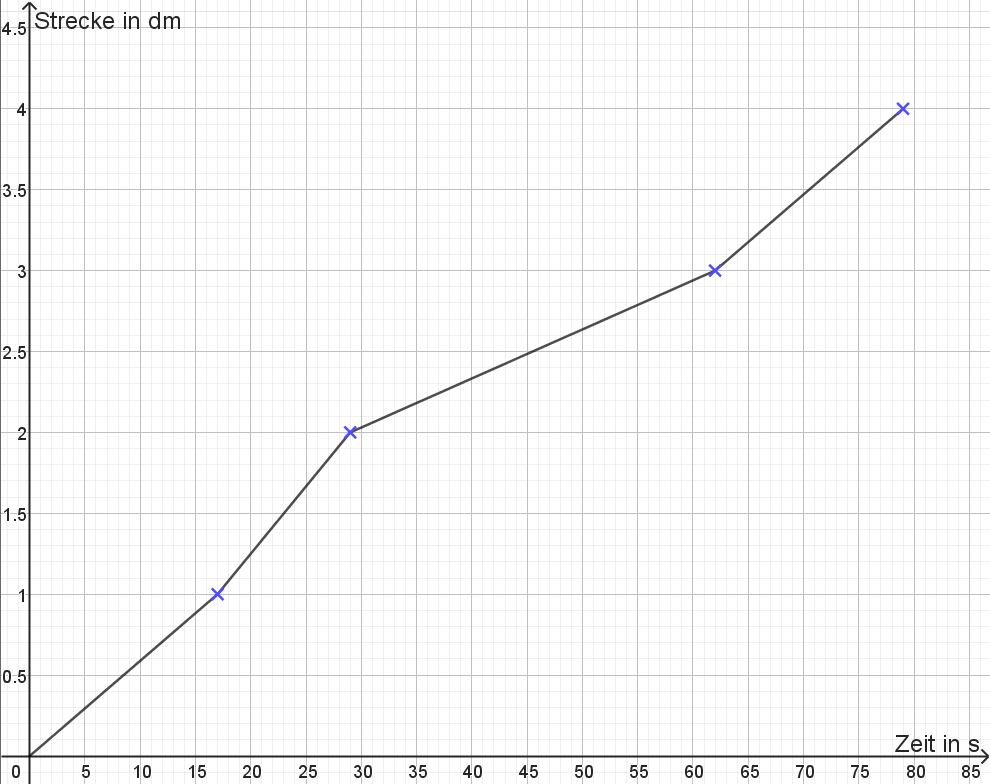
Die Aufgabe im Video lautet zu regelmäßigen zurückgelegten Strecken \(\Delta s\) die benötigten Zeitabstände \(\Delta t\) aufzunehmen. Insgesamt sind fünf Messpunkte zu sehen, also vier Abschnitte dazwischen mit jeweiligen Geschwindigkeiten. Werten Sie zunächst die drei Versuche gemäß der Anleitung im Video aus.
Hinweis: \( \Delta \) (Delta) steht für die Differenz zweier Messwerte, z.B. \(\Delta t=t_2 – t_1\).
Alternativ oder zusätzlich können Sie die Auswertung in dem folgenden Programm durchführen:
Versuch: Lösungen
Lösung durch Überlegen:
Bei \(v=60\frac{km}{h}\) legen Sie ja genau einen Kilometer pro Minute zurück. Mit \(v=120\frac{km}{h}\) ist man also doppelt so schnell und schafft zwei Kilometer pro Minute -> 500 Meter werden also in einer Viertelminute zurückgelegt.
Lösung durch Rechnung:
Es gilt \(v=\frac{s}{t} \), also \(t=\frac{s}{v}\), außerdem besteht eine Stunde aus 60 Minuten und jede Minute aus 60 Sekunden:
\(1\:h=60\:min=3600\:s\)
Mit eingesetzten Werten ist \(t=\frac{500\:m}{120\frac{km}{h}}=\frac{500\:m}{120\frac{1000\:m}{3600\:s}}=\frac{500\:m}{120\frac{m}{3{,}6\:s}}=15\:s\).
Versuch 1:
| Messung | 1 | 2 | 3 | 4 | 5 |
| Zeitstempel in \(s\) | 12 | 28 | 44 | 60 | 77 |
| Höhe \(s\) in \(dm\) | 0 | 1 | 2 | 3 | 4 |
| \(\Delta t\) in \(s\) | 0 | 16 | 16 | 16 | 17 |
| \(\Delta s\) in \(m\) | 0 | 0,1 | 0,2 | 0,3 | 0,4 |
| \(\frac{\Delta s}{\Delta t}\) in \(\frac{m}{s}\) | \(\frac{0{,}1}{16}\) | \(\frac{0{,}1}{16}\) | \(\frac{0{,}1}{16}\) | \(\frac{0{,}1}{17}\) | |
| \(\frac{s}{t}\) in \(\frac{m}{s}\) | \(0{,}00625\) | \(0{,}00625\) | \(0{,}00625\) | \(0{,}00588\) |
\( \)
Zeit-Weg-Diagramm: Im Rahmen der Messgenauigkeit handelt es sich um eine gleichförmige Bewegung.
Versuch 2:
| Messung | 1 | 2 | 3 | 4 | 5 |
| Zeitstempel in \(s\) | 95 | 125 | 154 | 182 | 210 |
| Höhe \(s\) in \(dm\) | 0 | 1 | 2 | 3 | 4 |
| \(\Delta t\) in \(s\) | 0 | 30 | 29 | 28 | 28 |
| \(\Delta s\) in \(m\) | 0 | 0,1 | 0,2 | 0,3 | 0,4 |
| \(\frac{\Delta s}{\Delta t}\) in \(\frac{m}{s}\) | \(\frac{0{,}1}{30}\) | \(\frac{0{,}1}{29}\) | \(\frac{0{,}1}{28}\) | \(\frac{0{,}1}{28}\) | |
| \(\frac{s}{t}\) in \(\frac{m}{s}\) | \(0{,}00333\) | \(0{,}00345\) | \(0{,}00357\) | \(0{,}00357\) |
\( \)
Zeit-Weg-Diagramm: Im Rahmen der Messgenauigkeit handelt es sich um eine gleichförmige Bewegung.
Versuch 3:
| Messung | 1 | 2 | 3 | 4 | 5 |
| Zeitstempel in \(s\) | 230 | 247 | 259 | 292 | 309 |
| Höhe \(s\) in \(dm\) | 0 | 1 | 2 | 3 | 4 |
| \(\Delta t\) in \(s\) | 0 | 17 | 12 | 33 | 17 |
| \(\Delta s\) in \(m\) | 0 | 0,1 | 0,2 | 0,3 | 0,4 |
| \(\frac{\Delta s}{\Delta t}\) in \(\frac{m}{s}\) | \(\frac{0{,}1}{17}\) | \(\frac{0{,}1}{12}\) | \(\frac{0{,}1}{33}\) | \(\frac{0{,}1}{17}\) | |
| \(\frac{s}{t}\) in \(\frac{m}{s}\) | \(0{,}00588\) | \(0{,}00833\) | \(0{,}00303\) | \(0{,}00588\) |
\( \)
Zeit-Weg-Diagramm: Das Objekt ändert seine Geschwindigkeit in jedem Abschnitt. Es handelt sich nicht um eine gleichförmige Bewegung.
Da die Kamera auf die mittlere gelbe Markierung ausgerichtet ist, sieht man schräg auf die oberen und unteren Markierungen. Dies nennt man Parallaxenfehler und führt zu falschen Ablesewerten z.B. bei Messgeräten mit Zeigern. Auch in diesem Experiment ist der Startzeitpunkt an der untersten gelben Markierung durch die Parallaxe schwer zu bestimmen.
Durch die Rotation der hinaufgezogenen Palette wird eine Ablesung zusätzlich erschwert.
Der Abstand zwischen den Markierungen kann nur ungenau z.B. über die Größe der Figur abgeschätzt werden.
Für die Zeitmessung liegt nur eine sekundengenaue Zeitskala von Youtube vor. Auch die Framerate des Videos ist ohne genauere Analyse unbekannt. In einem Videobearbeitungsprogramm könnte man die Zeitstempel für Start und Stop der Messung besser bestimmen.
Es ist nicht bekannt, ob durch den Motor und das Aufwickeln der Schnur eine gleichbleibende Geschwindigkeit beibehalten wird. (Der Umfang der Rolle wird größer, je mehr Schnur aufgewickelt wird. Bei einer Umdrehung wird also mehr oder weniger Schnur aufgewickelt, je nachdem, wie „voll“ die Rolle bereits ist. Außerdem wird die Last weiter oben geringer, da weniger Schnur gezogen werden muss.)