Mechanische Arbeit

Kraft und Arbeit

Wiederholung: Im Kapitel Kräfte wurde bereits darauf eingegangen, dass eine Kraft zur Verrichtung von Arbeit an einem Objekt nötig ist. Im Kranvideo aus dem früheren Kapitel wird ein Objekt hochgehoben. Auf das Bauteil wirkt die Gewichtskraft \(F_G=m \cdot g\). Diese Gewichtskraft muss überwunden werden, um das Bauteil hochzuziehen. Wenn das Bauteil um eine Höhe \(h\) angehoben wird, wird an dem Bauteil eine Arbeit \(W = F_G \cdot h=m \cdot g \cdot h\) verrichtet.

Für die mechanische Arbeit gilt allgemein die Definition:

\(Arbeit=Kraft \cdot Weg\), also \(W=F \cdot s\). Dabei ist wichtig, dass die Arbeit entlang des Weges verrichtet wird!

Die Einheit der physikalischen Arbeit ist das Joule \(J\): \([W]=1\:N\cdot m=1 \: \frac{kg \cdot m^2}{s^2}=1 \: J\)

Hubarbeit – Rechenbeispiel:

Hebt man einen Koffer der Masse \(m=22{,}7\:kg\) um die Höhe \(\Delta h=2{,}20\: m\) in ein Gepäckfach eines Zuges, so verrichtet man am Koffer die Arbeit

\(W_{Hub}=m \cdot g \cdot h=22{,}7\:kg \cdot 9{,}81 \: \frac{m}{s^2} \cdot 2{,}20\:m = 489{,}9114 \: \frac{kg \cdot m^2}{s^2}\approx 490 \: J = 0{,}490 \: kJ \)

Neben der gerade beschriebenen Hubarbeit gibt es beispielsweise auch die Beschleunigungsarbeit (Beschleunigendes Motorrad), die Spannarbeit (Aufziehen eines Spielzeugautos) oder Reibarbeit (Verschieben von Möbeln).

Reibarbeit auf waagrechtem Boden

Es gilt auch hier die allgemeine Definition der mechanischen Arbeit: \(Arbeit=Kraft \cdot Weg\)

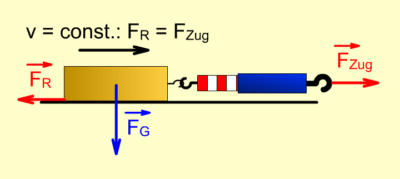
Für die physikalische Reibarbeit gilt ausschließlich der Weg, den man entgegen der Reibungskraft zurücklegt. Es wird nicht beachtet, dass das gezogene Objekt auch zunächst beschleunigt und wieder abgebremst werden muss. Ob man also schneller oder langsamer zieht, ist in unserem Fall für die Reibarbeit egal.

Es gilt somit die Formel \(W=F_R \cdot s\).

Die Reibungskraft hängt von der Reibungszahl \(\mu\) und der Kraft des Objekts auf die Oberfläche ab:

\(W=\mu \cdot F_G \cdot s\)

Mit \(F_G=m \cdot g\) ist die Formel für die Reibarbeit

\(W_{Reib}=\mu \cdot m \cdot g \cdot s\)

Reibarbeit – Rechenbeispiel

Sie möchten Ihre Couch der Masse \(m=87{,}3\:kg\) um \(s=7{,}5\:m\) in Ihrem Wohnzimmer verschieben. Wir berechnen die dafür benötigte Arbeit, wenn dies auf a) Fliesen mit \(\mu=0{,}12\) oder auf b) Teppich mit \(\mu=0{,}37\) geschieht:

a) \(W_{Reib}=\mu \cdot m \cdot g \cdot s=0{,}12 \cdot 87{,}3\:kg \cdot 10 \: \frac{N}{kg} \cdot 7{,}5\:m=785{,}7\:N\:m\approx 0{,}79\: kJ\)

b) \(W_{Reib}=\mu \cdot m \cdot g \cdot s=0{,}37 \cdot 87{,}3\:kg \cdot 10 \: \frac{N}{kg} \cdot 7{,}5\:m=2422{,}575\:N\:m\approx 2{,}4\: kJ\)

Die geneigte Ebene – Kombination von Hub- und Reibarbeit

Wie schon früher erwähnt gehört die geneigte Ebene zu den sogenannten „Einfachen Maschinen“, mit denen man sich Arbeit erleichtern kann. So können auch Fahrzeuge, die keinen Allrad-Antrieb haben, auf Serpentinen den Berg hinauf gelangen. Die geneigte Ebene machten sich aber auch schon die alten Ägypter beim Bau der Pyramiden zu Nutze. Heute werden Rampen natürlich ebenfalls eingesetzt, beispielsweise auf Baustellen für Schubkarren.

In der Grundeinstellung besitzt die geneigte Ebene hier im Applet einen Steigungswinkel von \(\alpha=29{,}3^{\circ}\) und überwindet einen Höhenunterschied von \(h=5{,}0\:m\). Das Applet können Sie hier finden, um es auf einer eigenen Seite zu öffnen.

Die auf der schiefen Ebene liegende Masse \(m = 1{,}00\: kg\) besitzt eine Gewichtskraft von \(F_G=m \cdot g= 1{,}00\: kg \cdot 10{,}0\:\frac{N}{kg}=10{,}0\:N\). Dieser Wert ist festgelegt und ändert sich somit bei keiner Einstellung im Applet. Die Berechnungen der Normal- und Hangabtriebskraft kennen wir aus dem vorherigen Kapitel:

\(F_H=m \cdot g \cdot sin(\alpha)= 1{,}00\: kg \cdot 10{,}0\:\frac{N}{kg} \cdot sin(29{,}3^{\circ})\approx 4{,}89\:N\) (Vergleichen Sie mit der App.)

\(F_N=m \cdot g \cdot cos(\alpha)= 1{,}00\: kg \cdot 10{,}0\:\frac{N}{kg} \cdot cos(29{,}3^{\circ})\approx 8{,}72\:N\) (Vergleichen Sie mit der App.)

Aus der Normalkraft berechnet sich die Reibungskraft \(F_R=\mu \cdot F_N\), die aber zunächst auf Null gesetzt wurde.

Da sich das Kräftedreieck und die geneigte Ebene gleichen, kann man aus dem Winkel \(\alpha\) und der Höhe \(h\) auch die Länge der Ebene \(l\) und die Länge der Grundseite \(b\) ausrechnen.

Goldene Regel der Mechanik

Ohne Reibung ist es gleichgültig auf welchem Weg man die Kiste auf den höchsten Punkt der geneigten Ebene bekommt.

Hebt man die Kiste hoch gilt:

\(W_{Hub}=F_G \cdot h=10{,}0\:N \cdot 5{,}00\:m=50\:J\)

Zieht man sie die geneigte Ebene hoch gilt:

\(W_{geneigt}=F_H \cdot l=4{,}89\:N \cdot 10{,}22\:m\approx 50\:J\)

Man kann sich also die Kraft reduzieren, um die Kiste die geneigte Ebene hinaufzubekommen, man muss dann allerdings einen längeren Weg in Kauf nehmen. Es hilft nichts: Die Arbeit an der Kiste muss schließlich verrichtet werden. Diese Regel gilt als die „Goldene Regel“ der Mechanik:

„Was an Kraft eingespart wird, muss an Weg zugesetzt werden.“

Wir werden auf der nächsten Seite eine weitere einfache Maschine kennenlernen, die nach diesem Prinzip arbeitet: Den Flaschenzug.

Geneigte Ebene mit Reibung

Die Reibung an der geneigten Ebene ist tatsächlich etwas wankelmütig: Sie wirkt immer der Bewegung entgegen. Sie kann also sowohl nach oben wirken und den Körper vom Hinabrutschen abhalten, als auch gemeinsam mit der Hangabtriebskraft nach unten wirken, wenn man den Körper nach oben ziehen möchte.

Setzen Sie das obige Applet zurück. Drücken Sie dann auf die Schaltfläche „Gummi Eis“ und erhöhen Sie die Zugkraft nach oben ein wenig (Regler rechts).

Sie erkennen sofort, dass sich der Wert für die Arbeit von \(W=50\:J\) auf \(W=67{,}82\:J\) erhöht hat. Um den Körper die schiefe Ebene hochzuziehen, muss man nun sowohl die Hangabtriebskraft als auch die Reibungskraft überwinden. Somit erhöht sich die zu verrichtende Arbeit durch die Reibungskraft:

\(F_R=\mu \cdot F_N=0{,}200 \cdot 8{,}72\:N\approx 1{,}74\:N\)

\(W_{geneigt}=(F_H + F_R)\cdot l=(4{,}89\:N+1{,}74\:N) \cdot 10{,}22\:m\approx 67{,}8\:J\)

Da die Gewichtskraft \(F_G\) allerdings immer noch größer ist als die Hangabtriebskraft \(F_H\) und die Reibungskraft \(F_R\) zusammen, lohnt sich die geneigte Ebene trotzdem. Die Kraft, die zum Hochschieben benötigt wird, ist nun ungefähr \((F_H + F_R)\approx 6{,}63\:N\). Man muss zwar jetzt insgesamt mehr Arbeit verrichten, allerdings ist die aufzuwendende Kraft immer noch weniger als das direkte Hochheben mit \(F_G=10{,}0\:N\).

Stellen Sie den Kraft-Regler auf \(F=6{,}6\) und \(F=6{,}7\). Sie stellen fest, dass \(F=6{,}6\:N\) nicht ausreichen, um die Kiste nach oben zu schieben. Erst ab einer Kraft von \(F=6{,}7\:N\) überwindet man die gemeinsame Hangabtriebs- und Reibungskraft.

Geneigte Ebene – Übung

Nutzen Sie nun das Applet: Stellen Sie verschiedene Neigungswinkel \(\alpha\) und Reibungszahlen \(\mu\) ein.

• Rechnen Sie jeweils die Kräfte sowie die zu verrichtende Arbeit beim Hochschieben des Körpers nach.
• Vergleichen Sie diese Arbeit jeweils mit der direkten Hubarbeit (gegebenenfalls ausrechnen!).
• Finden Sie jeweils die Kraft heraus, mit der man den Körper die geneigte Ebene hinaufschieben könnte.
• Überlegen Sie sich in jedem einzelnen Fall, ob die geneigte Ebene hier sinnvoller als das direkte Hochheben ist.