Kräftepläne
Kräfteaddition: Vier Hühner an der Leine
Statische Probleme können sehr gut mit Hilfe von Kräftesystemen und Kräfteplänen veranschaulicht werden. Max und Moritz erster Streich von Wilhelm Busch (1832 -1908) kann in ein Kräftesystem umgesetzt werden. In dieser Geschichte fressen drei Hühner und ein Hahn gierig die an Stricken befestigten Köder und können sich danach nicht mehr befreien, so sehr sie auch in alle vier Richtungen zerren. Eine Erzählung der Geschichte können Sie beispielsweise hier finden.
Wird die Szene von oben betrachtet und geht man zunächst von gleich kräftigen Hühnern aus, so kann folgendes Kraftsystem gezeichnet werden. Dieses System soll hinsichtlich der Frage untersucht werden, mit welcher resultierenden Kraft \(F_{res}\) der Punkt P in welche Richtung gezogen wird.
Verändern Sie in folgendem Applet die Stärke und die Richtung, mit der jedes Huhn (oder Hahn) an den Fäden zieht. Ein längerer Pfeil entspricht demnach einer größeren Kraftanstrengung des jeweiligen Tiers. Der addierte Kraftvektor gibt die resultierende Kraft \(F_{res}\) an, und zeigt somit in die Richtung, in die sich der Punkt P (und auch das Gesamtsystem) bewegen würde. Sie können den Punkt P entlang der resultierenden Kraft bewegen:
Sie können das Applet hier auf einer eigenen Seite im Browser öffnen.
Vektorpfeile können zusammengezählt werden, indem man sie aneinanderlegt. Im obigen Hühner-Beispiel hat Geogebra diese Addition selbständig für uns durchgeführt, um uns die (addierte) resultierende Kraft anzuzeigen. Diese Addition von zwei oder mehr Kräften kann auch von uns durchgeführt werden, wobei man entweder zeichnerisch oder rechnerisch an das Problem herangeht:
Kräfteaddition: Zeichnerische Lösung
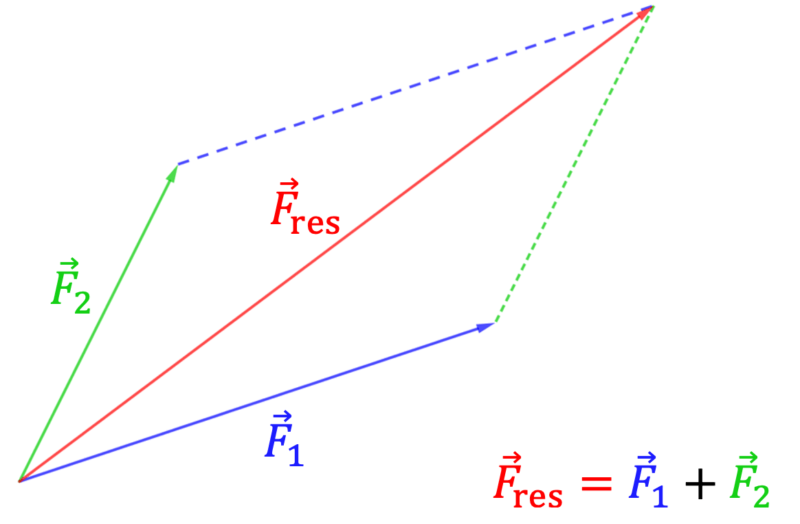
Voraussetzung für die zeichnerische Lösung ist, dass alle Kräfte mit ihrem richtigen Betrag (Länge des Vektors) und dem richtigen Lagewinkel von dem gemeinsamen Punkt P abgetragen werden. Zwei Kräfte, die an einem gemeinsamen Punkt P ansetzen, können durch eine resultierende Kraft ersetzt werden. Die resultierende Kraft ergibt sich aus der Parallelverschiebung des zweiten Vektors an die Spitze des ersten Vektors. Mit den beiden weiteren Vektoren wird ebenso verfahren.
Sie können das Applet hier auf einer eigenen Seite im Browser öffnen.
Kräfteaddition: Rechnerische Lösung
Zwei Kräfte, die auf derselben Wirkungslinie liegen, dürfen unmittelbar addiert werden. Die Richtung gibt dabei das Vorzeichen an. Ansonsten ist es möglich, alle Kräfte in ihre \(x\)-Komponente und \(y\)-Komponente aufzuteilen:
\(F_{1x}=cos(\alpha)\cdot F_1\)
\(F_{1y}=sin(\alpha)\cdot F_1\)
\(F_{2x}=cos(\beta)\cdot F_2\)
\(F_{2y}=sin(\beta)\cdot F_2\)
Da diese Einzelkomponenten jeweils in dieselben Richtungen (\(x\) und \(y\)) zeigen ist es nun möglich, sie einfach jeweils zusammenzuzählen.
Es gilt also getrennt für die \(x\)- und \(y\)-Komponenten des resultierenden Vektors:
\(F_x=F_{1x}+F_{2x}\)
\(F_y=F_{1y}+F_{2y}\)
Letztendlich werden die addierten \(x\)- und \(y\)-Komponenten mit dem Satz des Pythagoras zur endgültigen resultierenden Kraft zusammengesetzt:
\(F_{res}=\sqrt{F_{x}^2+F_{y}^2}\)
Den resultierenden Winkel kann man über den Tangens ermitteln:
\(tan(\gamma)=\frac{F_y}{F_x}\)
Achtung: Die Winkel müssen nicht immer von der x-Achse in mathematisch positiver Richtung abgetragen sein.
Mit den Kräften \(F_3\) und \(F_4\) aus dem Hühnerbeispiel müsste nun ebenso verfahren werden. Es ist leicht einzusehen, dass eine zeichnerische Lösung oft der schnellere Weg zu einem ungefähren Ergebnis ist.
Kräfteaddition: Kräfte beim Bogenschießen
Ein weiteres Beispiel ist die resultierende Kraft beim Bogenschießen. Die beiden gespannten Seile üben jeweils eine Kraft schräg nach oben links und nach oben rechts aus. Zusammenaddiert entsteht eine Kraft \(\vec{F}_{res}\), die geradeaus auf den Pfeil wirkt. Natürlich muss die Hand mit dem gleichen Kraftbetrag nach unten ziehen, um den Bogen zu spannen. Diese ist hier im Video allerdings nicht eingezeichnet.
Es wird auch deutlich, dass der Maßstab der Kraftvektoren nichts mit der realen Geometrie zu tun hat: \(\vec{F}_{res}\), \(\vec{F}_{S1}\) und \(\vec{F}_{S2}\) sind in keinerlei Hinsicht durch die Länge der Seile oder des physischen Pfeils beeinflusst. Die jeweilige Länge dieser Vektoren gibt ausschließlich die Stärke der Kraft wider. Der Kräfteplan (\(\vec{F}_{res}\), \(\vec{F}_{S1}\), \(\vec{F}_{S2}\)) und die reale Geometrie (Seile, Pfeil) besitzen allerdings die gleichen Winkel. Die Physik erfindet also quasi den Kräfteplan zur Realität hinzu, um den Vorgang rechnerisch oder zeichnerisch beschreiben zu können:
Kräfteaddition: Übungsaufgabe
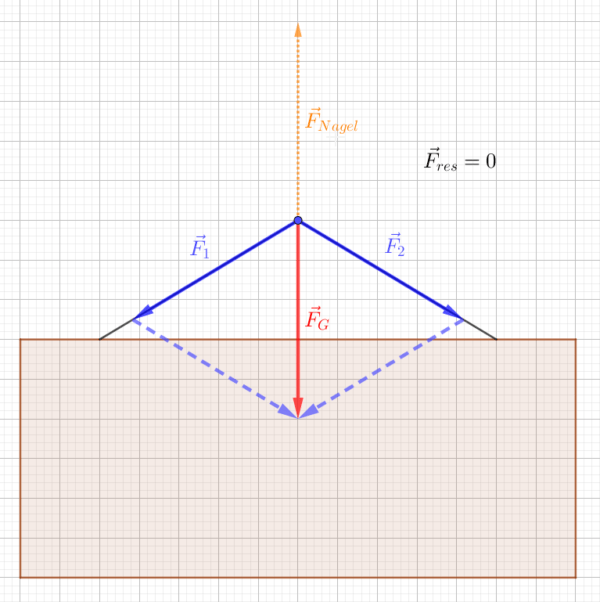
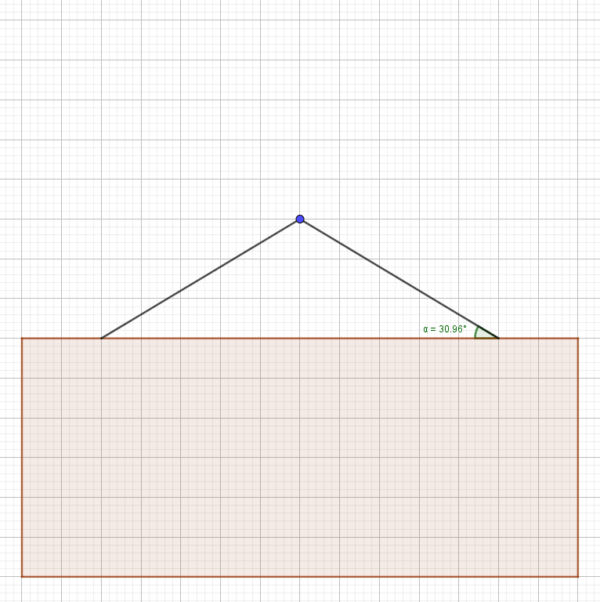
Ein 70 Zentimeter breites Bild der Masse 5,0 kg hängt an einer Schnur, die jeweils 10 Zentimeter rechts und links vom Rand am oberen Rahmen festgemacht ist. Die Schnur wird dann über einen Nagel gehängt, der 15 Zentimeter über dem Bild in der Wand befestigt ist. Die Zeichnung ist maßstabsgetreu. Ermitteln Sie zeichnerisch, wie viel Kraft das Bild auf die beiden schrägen Seilstücke rechts und links ausübt.
Hinweis: Verwenden Sie in der Gleichung \(F_G=m \cdot g\) zur Vereinfachung den Ortsfaktor \(g=10\:\frac{N}{kg}\).
Man berechnet zuerst den Betrag der Gewichtskraft \(\vec{F}_G\) des Bildes:
\(F_G=5{,}0\:kg \cdot 10\: \frac{N}{kg}=50\:N\)
Es bietet sich an, die Gewichtskraft von 50 Newton mit einem Kraftpfeil von 5,0 Zentimetern und am Nagel beginnend darzustellen:
Maßstab \(10\:N \: \widehat{=} \: 1{,}0\:cm\)
Die beiden Kräfte am Seil \(\vec{F}_{1}\) und \(\vec{F}_{2}\) sind symmetrisch und müssen dann gemeinsam die Gewichtskraft \(\vec{F}_{G}\) ergeben.
Bemerkung: Der Nagel muss natürlich das Gewicht des Bildes halten. Insgesamt addieren sich also alle Kräfte zu Null (wie bei den gleich starken Hühnern), das Bild bewegt sich ja schließlich nicht.
Misst man dann beispielsweise die Länge des Vektors \(\vec{F}_{1}\) nach, so erhält man für diesen ca. 4,86 Zentimeter.
Das bedeutet, dass Bild zieht an beiden Seilstücke rechts und links jeweils mit der Kraft 48,6 Newton (also ca. 49 N):
Kräftezerlegung: Die geneigte Ebene
Das bekannteste Beispiel für Kräftezerlegung ist die Aufteilung der Gewichtskraft \(\vec{F}_G\) eines Objekts auf einer geneigten (bzw. schiefen) Ebene. Die geneigte Ebene gehört zu den sogenannten „Einfachen Maschinen“ in der Mechanik, um sich aufzuwendende Arbeit zu erleichtern.
Möchte man beispielsweise mit dem Auto auf einen Berg fahren, so wird das Fahrzeug den direkten Weg kaum schaffen. Gewundene Bergstraßen, sogenannte Serpentinen, sind zwar deutlich länger als der direkte Weg, aber deswegen auch deutlich weniger steil.
Im Kräfteplan wird der Vektor der Gewichtskraft \(\vec{F}_G\) in zwei Vektoren aufgeteilt: Ein Teil drückt weiterhin senkrecht auf die Oberfläche, man nennt diese die Normalkraft \(\vec{F}_N\) des Objekts. Der andere Teil beschleunigt das Objekt den Hang hinab, weswegen sie auch Hangabtriebskraft \(\vec{F}_H\) genannt wird.
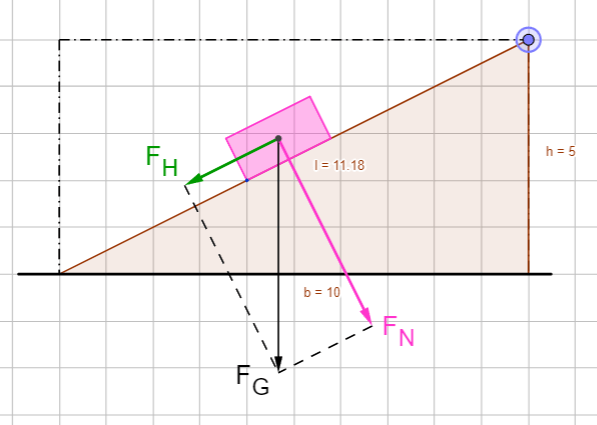
Bei der Aufteilung der Gewichtskraft spielt die Neigung der Ebene die entscheidende Rolle, es entsteht aber in jedem Fall ein rechtwinkliges Dreieck. Der Winkel der geneigten Ebene gegenüber dem Boden ist auch immer ein Winkel im (ausgedachten) Kräftedreieck.
In der Animation weiter unten sind besonders die Extreme auffällig: Besitzt die Ebene keine Neigung, so sind Normalkraft und Gewichtskraft identisch, also \(\vec{F}_N=\vec{F}_G\). Ist die Neigung der Ebene senkrecht zum Boden, so rutscht das Objekt nicht mehr hinab, sondern fällt einfach an der Ebene vorbei zu Boden. Das bedeutet, dass die Hangabtriebskraft und die Gewichtskraft identisch sind, also \(\vec{F}_H=\vec{F}_G\).
Da das rechtwinklige Kräftedreieck immer auf dieselbe Art und Weise entsteht, gibt es feste Formeln für Hangabtriebs- und Normalkraft. Wenn der Neigungswinkel \(\alpha\) der geneigten Ebene gegenüber dem Boden bekannt ist, dann gilt:
\(\vec{F}_H=\vec{F}_G \cdot sin(\alpha)\) und
\(\vec{F}_N=\vec{F}_G \cdot cos(\alpha)\),
Zusätzlich interessiert bei solchen Aufgaben auch die Wirkung der Reibungskraft \(\vec{F}_R\). Da die Reibung immer mit der Kraft des Objekts auf die Oberfläche zu tun hat, ist sie also abhängig von der Normalkraft \(\vec{F}_N\) und der sogenannten Reibungszahl \(\mu\). Es gilt:
\(\vec{F}_R=\vec{F}_N \cdot \mu\)
Kräftezerlegung: Rechenbeispiel zur geneigten Ebene
Gegeben: Auf einer geneigten Ebene mit dem Winkel \(\alpha=35{,}0^{\circ}\) gegenüber dem Boden liegt eine Kiste der Masse \(m=25{,}0\:kg\). Die Reibungszahl zwischen Oberfläche und Kiste beträgt \(\mu=0{,}180\). Zur Vereinfachung soll mit \(g=10{,}0\:\frac{N}{kg}\) gerechnet werden.
Gesucht: Berechnen Sie alle Kräfte und beurteilen Sie, ob die Kiste liegen bleibt.
Lösung:
Die Gewichtskraft der Kiste beträgt \(F_G=m \cdot g=25{,}0\: kg \cdot 10{,}0\:\frac{N}{kg}=250\:N\).
Somit berechnen sich \(F_N\) und \(F_H\) zu
\(F_N= F_G \cdot cos(\alpha)=250\: N \cdot cos(35{,}0^{\circ})\approx 205\:N\)
\(F_H= F_G \cdot sin(\alpha)=250\: N \cdot sin(35{,}0^{\circ})\approx 143\:N\)
Die Reibungskraft kann man aus der Normalkraft berechnen:
\(F_R= F_N \cdot \mu=205\: N \cdot 0{,}180\approx 36{,}9\:N\)
Man sieht, dass die Hangabtriebskraft mit 143 Newton größer ist als die Reibungskraft mit 36,9 Newton. Das bedeutet, dass die Kiste in diesem Fall herunterrutschen würde.
Zusatzfrage: Wie groß müsste die Reibungszahl also sein, damit die Kiste liegen bleibt?
Lösung:
Damit die Kiste liegen bleibt müsste die Reibungskraft genauso groß sein wie die Hangabtriebskraft \(F_H\) mit 143 N, es gilt also
\(F_R= F_H\)
\(F_N \cdot \mu = 143\:N\)
\(250\:N \cdot \mu = 143\:N \;\; |:250\:N\)
\(\mu\approx 0{,}572\)
Die Reibungszahl müsste also deutlich höher sein, damit die Kiste liegen bleibt.
Mit der Reibungszahl und deren Auswirkung auf die Arbeit, die man an der schiefen Ebene verrichten muss, beschäftigen wir uns auch auf der nächsten Seite.