Kräfte und Erdanziehung

Die Kraft \(F\) ist eine weitere zentrale physikalische Größe. Die Wirkung von Kräften kann täglich beobachtet werden:

• Eine Kraft kann einen Körper verformen, dies kann z.B. beim Schmieden von Metallen beobachtet werden, bei der Deformation eines Knetstückchens oder auch beim Zerschneiden von Butter.
• Eine Kraft kann einen Körper beschleunigen, es kommt zu einer Änderung der Geschwindigkeit oder einer Richtungsänderung, beim Autofahren wird es als ‚Gas geben‘ → positive Beschleunigung und ‚bremsen‘ → negative Beschleunigung bezeichnet.

Auf der Erde fallen alle Körper nach unten und beschleunigen in die Richtung des Erdmittelpunkts. Die Ursache ist die Gravitationskraft, d.h. die Massen zweier Körper ziehen sich an. In diesem Fall also beispielsweise die Masse eines Apfels und die Masse der Erde, so dass der Apfel vom Baum auf den Boden fällt. Die Beschleunigung, mit der der Apfel schneller wird, lässt sich experimentell ermitteln (siehe weiter unten).

Eigenschaften der physikalischen Kraft

Nach dem zweiten Newton’schen Gesetz gilt für Kräfte

\(F = m \cdot a\), mit \(a\) als Beschleunigung (englisch „Acceleration“).

Die Einheit der Kraft ist das Newton \(N\), benannt nach dem berühmten Physiker. Die Kraft \(\vec{F}\) hat in der Physik immer eine Richtung, man spricht deswegen von einer „vektoriellen Größe“. In der Mathematik versteht man unter einem Vektor einen Pfeil mit Startpunkt, Richtung und Länge. Damit hat die physikalische Kraft drei Eigenschaften:

• einen Angriffspunkt                                 („Wo greift die Kraft an?“)
• eine Richtung und                                    („In welche Richtung wirkt die Kraft?“)
• einen Betrag (bzw. eine Pfeillänge).      („Wie stark wird gezogen oder gedrückt?“)

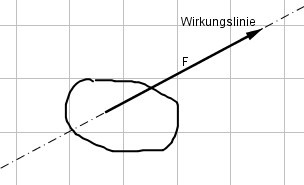
Die Kraft setzt an einem Angriffspunkt an und wirkt in eine Richtung mit einem bestimmten Betrag (Pfeillänge). Sie kann somit gut als Vektor sichtbar gemacht werden. Verlängert man den Vektor in beide Richtungen, so erhält man die Wirkungslinie der Kraft. In der Physik werden Vektoren mit einem Pfeil über dem Formelzeichen gekennzeichnet.

\( \vec{F}=m \cdot \vec{a}\)

In vielen Lehrbüchern wird dieser Pfeil weggelassen, so auch in diesem Lernbereich, trotzdem wissend, dass Kräfte Vektorpfeile mit Richtung und Länge sind!

Für die Gewichtskraft ergibt sich damit:

\(F_G=m \cdot g\), mit \(g\) als Ortsfaktor oder Erdbeschleunigung.

Der Wert für \(g\) beträgt \(g = 9{,}81 \: \frac{m}{s^2}\), es wird aber auch häufig vereinfacht mit \(g \approx 10 \: \frac{m}{s^2}\) gerechnet. Die Gewichtskraft setzt immer im Schwerpunkt eines Körpers an.

Die Erdanziehungskraft – Messung

Die Erdanziehungskraft – Auswertung

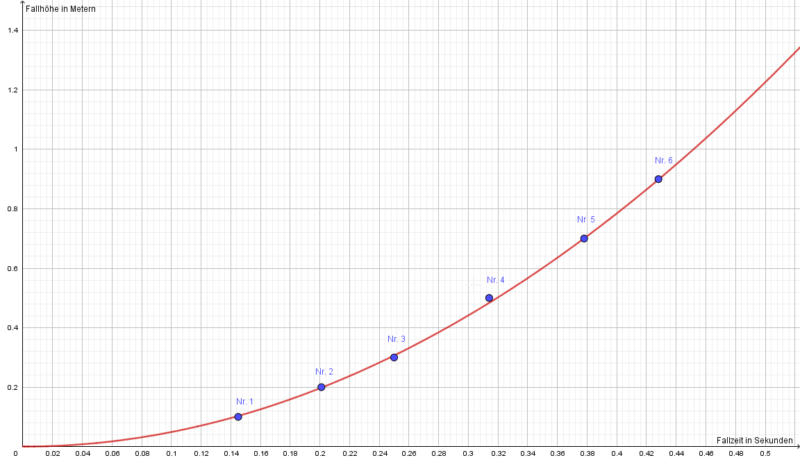
Trägt man die Werte der sechs Fallversuche in ein Fallzeit-Fallhöhe-Diagramm (\(t-h-Diagramm\)) ein, so sieht man, dass für eine doppelte Fallhöhe nicht die doppelte Fallzeit benötigt wird: Die Kugel wird bei größerer Fallhöhe immer schneller, was beim Herunterfallen ja tatsächlich zu erwarten ist.

Würde man in jedem der sechs durchgeführten Versuche die Geschwindigkeit der Kugel beim Aufprall messen, so würde man in einem Zeit-Geschwindigkeits-Diagramm (\(t-v-Diagramm\)) die folgenden Werte erhalten:

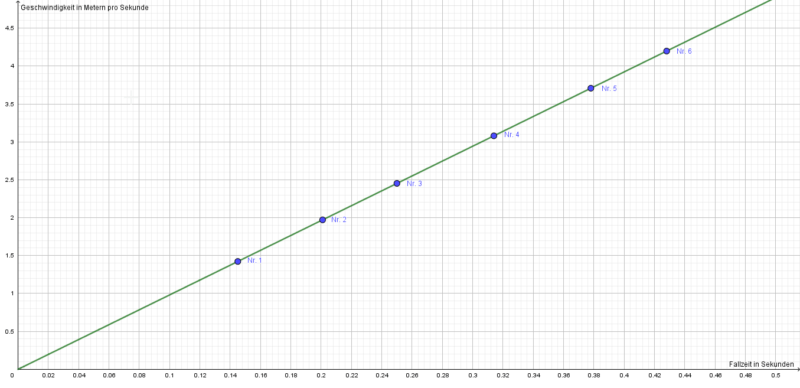
Betrachtet man die Auswertung des Versuchs, so zeigt sich, dass die Kugel mit zunehmender Fallhöhe und größer werdenden Fallstrecken \(\Delta s\) auch immer schneller wird.

Die Geschwindigkeit der Kugel \(v\) steigt nach der Formel \(v(t) = g \cdot t\) linear an, wobei \(g= 9{,}81 \: \frac{m}{s^2}\) die Erdbeschleunigung darstellt und im Fallversuch an der Erdoberfläche konstant ist. Dies bedeutet, dass ein Körper nach einer Sekunde im freien Fall bereits eine Geschwindigkeit von \(v(1\:s)=9{,}81 \: \frac{m}{s^2} \cdot 1\: s = 9{,}81 \: \frac{m}{s}\) besitzt – und nach zwei Sekunden schon \(v(2\:s)\approx 19{,}6 \: \frac{m}{s}\). Natürlich ist hier der Luftwiderstand nicht eingerechnet, der die Beschleunigung des Körpers verlangsamen würde.

Die zugehörige Kraft, die einen Körper auf der Erde nach unten beschleunigt, wird als Gewichtskraft \(F_G\) bezeichnet.

Kraft und Arbeit

Eine Kraft ist auch erforderlich, um an einem Körper Arbeit zu verrichten. Im Kranvideo aus dem vorherigen Kapitel wird ein Objekt hochgehoben. Auf das Bauteil wirkt die Gewichtskraft \(F_G=m \cdot g\). Diese Gewichtskraft muss überwunden werden, um das Bauteil hochzuziehen. Wenn das Bauteil um eine Höhe \(h\) angehoben wird, wird an dem Bauteil eine Arbeit \(W = F_G \cdot h=m \cdot g \cdot h\) verrichtet.

Neben der gerade beschriebenen Hubarbeit gibt es beispielsweise auch die Beschleunigungsarbeit (Beschleunigendes Motorrad), die Spannarbeit (Aufziehen eines Spielzeugautos) oder Reibarbeit (Verschieben von Möbeln).

Beispiel:

Steigt man auf einen Sprungturm der Höhe zehn Meter, so muss ein Mensch mit der Masse \(m=65\:kg\) die Arbeit

\(W_{Hub}=65\:kg \cdot 9{,}81 \: \frac{m}{s^2} \cdot 10\:m = 6376{,}5 \: \frac{kg \cdot m^2}{s^2}\approx 6{,}4 \cdot 10^3 \: J = 6{,}4 \: kJ \)

verrichten. Die Einheit der physikalischen Arbeit ist das Joule \(J\): \([W]=1 \: \frac{kg \cdot m^2}{s^2}=1 \: J\)