Der Flaschenzug
Auch in diesem Kapitel soll Hubarbeit verrichtet werden. Außer mit der geneigten Ebene und beispielsweise einem Hebel kann man zur Arbeitserleichterung dafür auch einen Flaschenzug verwenden. Dafür wird der anzuhebende Körper an ein Seil befestigt, welches dann über Rollen verläuft. Eine solche Anordnung besteht aus sogenannten „losen“ und „festen“ Rollen. Bei unseren Rechnungen vernachlässigen wir sowohl die Reibung des Seils an der Rolle, als auch das Eigengewicht der losen Rollen.
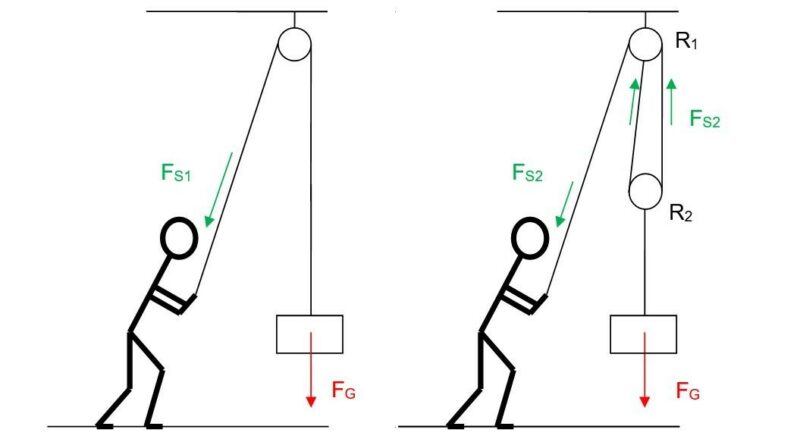
In der linken Abbildung wird ausschließlich eine feste Rolle verwendet, die an der Decke befestigt ist. Eine feste Rolle dient nur zur Umlenkung einer Kraft. Hier hat man beim Ziehen keinerlei Erleichterung, außer dass man nun natürlich die eigene Gewichtskraft zum Anheben ausnutzen kann. Es gilt also \(F_{S1}=F_G\). Diese Anordnung ist noch kein Flaschenzug.
In der rechten Abbildung ist eine lose und eine feste Rolle kombiniert. An der losen Rolle teilt sich die Gewichtskraft auf. Die eine Hälfte hängt am linken Seilstück, welches mit der festen Rolle oder der Decke verbunden ist. Nur die Hälfte, die am rechten Seilstück wirkt, wird zur ziehenden Person umgelenkt. Die Person muss also nur mit der Hälfte der Gewichtskraft am Seil ziehen: \(F_{S2}=\frac{1}{2} \cdot F_G\). Dies ist die einfachste Form des Flaschenzugs.
Da die Person in der rechten Abbildung durch das Ziehen am Seil allerdings nur das rechte Seilstück an der losen Rolle verkürzt, muss für das Anheben einer Höhe \(h\) die doppelte Länge an Seil gezogen werden: \(l=2 \cdot h\). Somit gilt auch hier die goldene Regel der Mechanik, dass der niedrigere Kraftaufwand mit einer größeren Weglänge bezahlt wird. Dies gilt natürlich auch für die verrichtete Hubarbeit:
| Allgemein gilt: \(W_{Hub}=F_G \cdot h\) | ||
| \(\:\) | ||
| \(W_{links}=F_{S1} \cdot s_1\) | \(W_{rechts}=F_{S2} \cdot s_2\) | |
| \(\:\) | ||
| Auf der linken Seite gilt:
\(F_{S1}=F_G\) und \(s_1=h\) |
Auf der rechten Seite gilt:
\(F_{S2}=\frac{1}{2} \cdot F_G\) und \(s_2=2 \cdot h\) |
|
| \(W_{links}=F_{G} \cdot h\) | \(W_{rechts}=\frac{1}{2} \cdot F_G \cdot 2 \cdot h\) | |
| \(W_{links}=F_{G} \cdot h\) | \(W_{rechts}= F_G \cdot h\) | |
| \(W_{links}=W_{rechts}\) | ||
| \(\:\) |
Ohne Beachtung der Reibung haben also beide Personen rechts und links die gleiche physikalische Arbeit verrichtet.
Das Prinzip des Flaschenzugs ist auch mit mehr Rollen einsetzbar. Mit jeder losen Rolle halbiert sich im Prinzip die aufzuwendende Kraft und verdoppelt sich der zu ziehende Seilweg. Auf der nächsten Seite finden Sie eine entsprechende Übung zu diesem Thema.
