Zufallsgröße, Binomialverteilung – Aufgaben
Testen Sie Ihr Wissen an folgenden Aufgaben
| 1 | Bei einem Spiel wird nacheinander an den folgenden Glücksrädern gedreht, bei denen jeder Sektor gleich groß ist.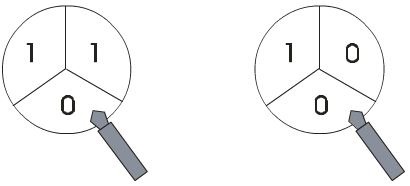
Erzielt man „01“, so bekommt man 10 Euro ausbezahlt, bei „00“ erhält man 5 Euro, bei „11“ 3 Euro, sonst gibt es keine Auszahlung. |
|
|---|---|---|
| 1.1 | Der Einsatz beträgt 2 Euro. Berechnen Sie Erwartungswert, Varianz und Standardabweichung der Zufallsgröße \(X\): Gewinn. | |
| 1.2 | Bestimmen Sie die Höhe des Einsatzes, damit das Spiel fair ist. | |
| 2 | Eine Laplace-Münze wird 10-mal geworfen. Die Zufallsgröße \(X\) gibt die Anzahl von Kopf an. | |
| 2.1 | Berechnen Sie Erwartungswert, Varianz und Standardabweichung der Zufallsgröße \(X\). | |
| 2.2 | Berechnen Sie die Wahrscheinlichkeit, dass die Anzahl von Kopf um höchstens das Doppelte der Standardabweichung vom Erwartungswert abweicht. | |
| 3 | Gegeben ist die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) mit \(a, b \in \mathrm{I\!R}\) durch \[\begin{array} {c|c} x & -1 & 0 & 0,5 & 2 & 4 \\ \hline P(X = x) & 0,1 & a & 2a & 0,2 & b \end{array}\]Weiter ist bekannt, dass der Erwartungswert \(µ = 2\) ist. |
|
| 3.1 | Berechnen Sie \(a\) und \(b\). | |
| 3.2 | Berechnen Sie Erwartungswert, Varianz und Standardabweichung der Zufallsgröße \(X\). | |
| 4 | Abschlussprüfung an Fachoberschulen 2003, Stochastik S1, Aufgabe 2: Bei der Untersuchung von Kiefernadeln wird die Länge \(L\) von 200 zufällig ausgewählten Nadeln bestimmt und in sechs Längengruppen eingeteilt. Die Zufallsgröße \(X\) gibt die Nummer der jeweiligen Längengruppe an. Dabei ergibt sich folgende Verteilung mit \(a, b \in \mathbb{N}\).\[\begin{array} {c|c} L \: in \: mm & L \leq 40 & 40 < L \leq 44 & 44 < L \leq 48 & 48 < L \leq 52 & 52 < L \leq 56 & L > 56 \\ \hline Längengruppe & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline Anzahl & 8 & a & 2a & 90 & b & 12 \end{array}\]Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Nadel in einer der Längengruppen 4 bis 6 liegt, beträgt dabei 0,66. |
|
| 4.1 | Berechnen Sie die Werte der Parameter \(a\) und \(b\). | |
| 4.2 | Erstellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(X\) und zeichnen Sie ein zugehöriges Histogramm. | |
| 4.3 | Bestimmen Sie, mit welcher Wahrscheinlichkeit die Zufallswerte innerhalb der einfachen Standardabweichung um den Erwartungswert liegen. |
