Venn-Diagramme
Ereignisse und deren Verknüpfungen lassen sich auch grafisch darstellen und bieten damit eine bessere Vorstellung. Hierfür nutzt man häufig Venn-Diagramme, benannt nach dem englischen Mathematiker John Venn. Ein Venn-Diagramm besteht hierbei aus einem Kasten, der den gesamten Ergebnisraum repräsentiert. Die Ereignisse werden anschließend durch jeweils eine Ellipse repräsentiert. Auf diese Weise kann man z.B. das Ereignis \(A\) und das Gegenereignis \(\overline A\) folgendermaßen darstellen:
Das Ereignis \(A\).
Das Gegenereignis zu \(A\), also \(\overline A =\Omega \backslash A\).
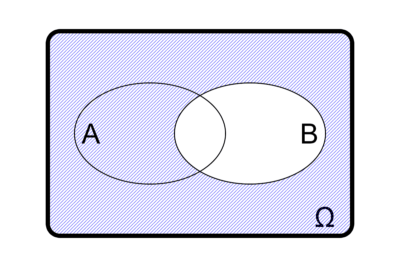
Möchte man nun mehrere Ereignisse in einem gemeinsamen Venn-Diagramm darstellen, so zeichnet man eine weitere Ellipse für das zweite Ereignis \(B\), die sich zum Teil mit der von \(A\) überlappt.
Auf diese Weise lassen sich nun auch die Verknüpfungen der Ereignisse grafisch repräsentieren:
Schnittmenge \(A\cap B\)
Derjenige Bereich, der in \(A\) und \(B\) liegt.
Vereinigungsmenge \(A\cup B\)
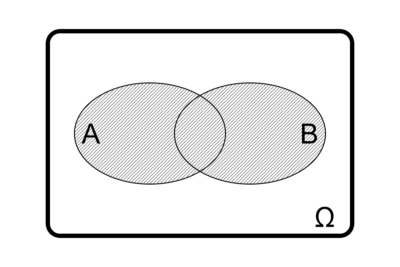
Derjenige Bereich, der in mindetens einer der Ellipsen liegt.
\(A \backslash B\) (=\(A\) ohne \(B\))
Derjenige Bereich, der in \(A\) aber nicht in \(B\) liegt.
Aufgabe
Eine andere Schreibweise für \(A\backslash B\) ist \(A\cap \overline B\). Weisen Sie diese Gleichheit durch geeignete Venn-Diagramme nach.
Hinweis: Fertigen Sie zunächst jeweils ein Venn-Diagramm für \(A\) bzw. \(\overline B\) an. Damit ein Ergebnis in \(A\cap \overline B\) liegt, muss es in \(A\) und \(\overline B\) liegen.
 |
 |
| Legt man diese beiden Venn-Diagramme nun übereinander und färbt die jeweiligen Teile ein, erhält man: |  |
| Damit ein Ergebnis nun in \(A\cap \overline B\) liegt, muss es in jedem der beiden Teile liegen. Es muss also rot und blau gefärbt sein. Übrig bleibt: |  |
Dies ist genau derjenige Teil des Venn-Diagramms, der in obigen Übersicht für \(A\backslash B\) markiert war. Es gilt also \(A\backslash B=A\cap \overline B\).