Die Punkt-Steigungs-Form
Herleitung der Punkt-Steigungs-Form
Im Kapitel „Grundlagen“ haben Sie bereits gesehen, dass der Term einer linearen Funktion in verschiedenen Formen vorkommen kann:
- Die Gleichung \(f(x) = m\cdot x+t \) heißt allgemeine Form der Funktionsgleichung (mit den Parametern für die Steigung \(m\) und den y-Achsenabschnitt \(t\)).
- Die Gleichung \(f(x) = m\cdot(x\ {-} \ x_0) + y_0 \) heißt Punkt-Steigungs-Form der Funktionsgleichung.
Bei der Punkt-Steigungs-Form werden
- die Steigung \(m\) der Geraden und
- ein beliebiger Punkt \(P(x_0\vert y_0) \) , der auf der Geraden liegt,
benötig.
Die Punkt-Steigungs-Form kann schnell hergeleitet werden, indem man die Koordinaten \(x_0\) und \(y_0\) des Punktes \(P\) in die allgemeine Form der Geradengleichung einsetzt:
\(1)\) Allgemeine Form: \(f(x)=m\cdot x+t\)
\( 2)\) \(P(x_0|y_0)\) liegt auf dem Graphen von \(f\). Also gilt:
\[f(x_0)=y_0\quad\Rightarrow\quad m\cdot x_0 +t=y_0\quad\Rightarrow\quad\color{red}{\boxed{\color{black}{t=y_0-m\cdot x_0}}}\]
Setzt man diesen Ausdruck für \(t\) wiederum in die allgemeine Form ein und fasst zusammen, so folgt:
\[f(x)=m\cdot x+\color{red}{t}=m\cdot x+\color{red}{y_0-m\cdot x_0}=m\cdot (x-x_0)+y_0\]
Die Punkt-Steigungs-Form ist offensichtlich insbesondere dann praktisch, wenn neben der Steigung ein Punkt einer linearen Funktion gegeben ist. Um die Funktionsgleichung aufzustellen, genügt es dann die gegebenen Informationen in die Punkt-Steigungs-Form einzusetzen und – falls gewünscht – auszumultiplizieren, um die allgemeine Form zu erhalten. Das Umwandeln in die allgemeine Form ist zum Beispiel nötig, falls man den \(y\)-Achsenabschnitt bestimmen möchte, da dieser in der Punkt-Steigungs-Form nicht direkt vorkommt.
Beispiel
Von einer linearen Funktion \(f\) ist bekannt, dass sie die Steigung \(m=-2\) besitzt und dass ihr Graph \(G_f\) durch den Punkt \(P(1\vert 4)\) verläuft. Bestimmen Sie die Funktionsgleichung der Funktion \(f\) und ermitteln Sie hiermit die Koordinaten des Schnittpunkts von \(G_f\) mit der \(y\)-Achse.
Zunächst stellen wir die Funktionsgleichung in der Punkt-Steigungs-Form auf. Durch Ausmultiplizieren gelangt man zur allgemeinen Form, anhand der man den Schnittpunkt mit der y-Achse ablesen kann:
\(f(x)=m\cdot (x-x_0)+y_0 =-2\cdot (x-1)+4=-2x+2+4=-2x+6\)
Folglich ist \(t=6\), und der Punkt \(S_y(0\vert6)\) ist der Schnittpunkt des Graphen von \(f\) mit der \(y\)-Achse.
Aufgaben
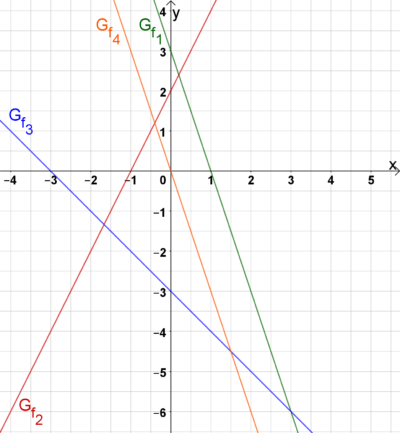
Bestimmen Sie zu den nachfolgenden Beispielen jeweils eine mögliche Funktionsgleichung, ermitteln Sie den jeweiligen \(y\)-Achsenabschnitt \(t\) und zeichnen Sie die zugehörigen Graphen in ein gemeinsames Koordinatensystem.
- \(m=-3, P(3|-6)\)
- \(m=2, P(-2|-2)\)
- \(m=-1, P(0|-3)\)
- \(m=-3,\) der Graph verläuft durch den Ursprung des Koordinatensystems.