Schnittpunkte quadratischer Funktionen
Schnittpunkte mit den Koordinatenachsen
Im nachfolgenden Koordinatensystem ist der Graph der Funktion \(f\) mit \(f(x)=0,5 x^2-4 x+6\) abgebildet. Gesucht sind der Schnittpunkt \(S_y\) des Graphen von \(f\) mit der \(y\)-Achse und die Schnittpunkte \(S_{x1}\) und \(S_{x2}\) mit der \(x\)-Achse.
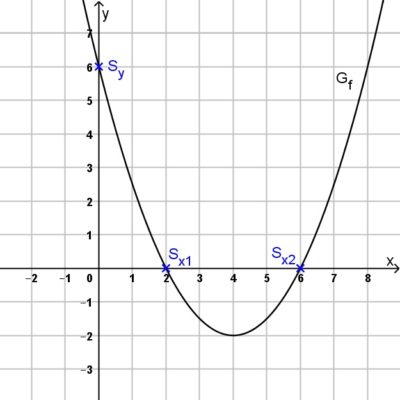
Schnittpunkte mit der \(y\)-Achse
Der Schnittpunkt \(S_y\) des Graphen mit der \(y\)-Achse ist über den Koeffizienten \(c\) der allgemeinen Form festgelegt, denn des gilt stets:
\[f(0)=a \cdot 0^2-b \cdot 0+c=c \quad \Rightarrow \quad S_y(0|c)\]
Beispielsweise erhält man für die Funktion \(f\) mit \(f(x)=0,5x^2-4x+6\):
\[f(0)=0,5 \cdot 0^2-4 \cdot 0+6=6 \quad \Rightarrow \quad S_y(0|6)\]
Schnittpunkt mit der \(x\)-Achse, Nullstellen
Ebenfalls wie bereits bei den linearen Funktionen, werden die Nullstellen über den Ansatz \(f(x)=0\) ermittelt. Hierbei gibt es eine spezielle Formel, auf deren Herleitung an dieser Stelle verzichtet wird.
Lösungsformel für quadratische Gleichungen ("Mitternachtsformel")
Die Lösungen der quadratischen Gleichungen \(a x^2 + b x +c=0\) besitzt …
… die beiden (einfachen) Lösungen \(x_{1/2} = \dfrac {-b \pm \sqrt{b^2-4 a c}} {2 a} \), falls die Diskriminante \(D=b^2-4 a c\) (Wert unter der Wurzel) positiv ist.
… die (doppelte) Lösung \(x=- \dfrac{b} {2 a} \), falls die Diskriminante \(0\) ist.
… keine Lösung, falls die Diskriminante negativ.
Schrittfolge
Im Beispiel
- Allgemeiner Ansatz: \(f(x)=0\)
- Lösungsformel anwenden
- Nullstellen \(x_1, x_2\) angeben
- Schnittpunkte mit der \(x\)-Achse
- \(f(x)=0 \Rightarrow 0,5 x^2-4x+6=0\)
- \(x_{1/2}=\dfrac{-(-4) \pm \sqrt{(4)^2-4 \cdot 0,5 \cdot 6}} {2 \cdot 0,5}=\dfrac{4 \pm 2}{1}\)
- \(x_1=2, x_2=6\)
- \(S_{x1}(2|0), S_{x2}(6|0)\)
Schnittpunkte von zwei Funktionen
Zusätzlich zur Funktion aus dem obigen Beispiel ist nun noch die Funktion \(g\) mit \(g(x)= – x^2+2 x+6\) gegeben. Die beiden Funktionsgraphen sind im folgenden Koordinatensystem dargestellt. Gesucht sind die Koordinaten der Schnittpunkte \(S_1\) und \(S_2\) der beiden Funktionsgraphen.
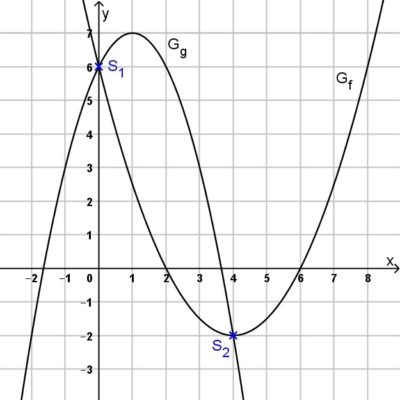
Der Ansatz zur Berechnung einer Schnittstelle der zwei Funktionen \(f\) und \(g\) lautet wiederum:
\[f(x)=g(x)\]
Auch hier ist das Ziel, dass man die Gleichung auf die Form \(x=\dots\) bringt.
Schrittfolge
Im Beispiel
- Allgemeiner Ansatz: \(f(x)=g(x)\)
- Terme auf eine Gleichungsseite bringen
- Werte für \(x\) berechnen
- \(0,5 x^2-4x+6=-x^2+2x+6\)
- \(1,5 x^2-6x+0=0\)
- \(x_{1/2}=\dfrac{-(-6) \pm \sqrt{(-6)^2-4 \cdot 1,5 \cdot 0}} {2 \cdot 1,5}=2 \pm 2\)
Somit ergeben sich im Beispiel die beiden Schnittstellen \(x_1=2-2=0\) und \(x_2=2+2=4\). Anschließend ergeben sich über den Funktionsterm die \(y\)-Koordinaten:
\[y_1=f(x_1)=0,5 \cdot 0^2-4 \cdot 0+6=6\Rightarrow S_1 (0\vert 6 )\]
\[y_2=f(x_2)=0,5 \cdot 4^2-4 \cdot 4+6=-2\Rightarrow S_2 (4\vert -2 )\]
Dabei ergeben sich, genau wie bei der Nullstellenberechnung, bis zu zwei Ergebnisse. Würde man nur einen Schnittpunkt der beiden Graphen erhalten, da die Diskriminante beim Ausrechnen \(0\) ergeben würde, spricht man von einem Berührpunkt.
Lösen von quadratischen Gleichungen
Manchmal benötigt man die Lösungsformel nicht und kann die quadratische Gleichung mit der passenden Methode wesentlich schneller lösen.
Gleichungen der Form \( a x^2+c=0\) durch Auflösen, z.B.:
\(2x^2-18=0 \)
\(2x^2=18 \)
\(x^2=9 \)
\(x= \pm 3 \)
Gleichungen der Form \(a x^2+b x=0\) durch Ausklammern, z.B.:
\(4x^2+20x=0 \)
\(4x(x+5)=0 \)
\( x_1=0\) und \(x_2=-5 \)
Übung
Berechnen Sie die Nullstellen der folgenden Funktionsterme:
a) \(f(x)=x^2+5x-14 \)
b) \(g(x)=-3x^2+9x+84 \)
c) \(h(x)=4x^2-3x+5 \)
d) \(i(x)=3x^2+8x \)
e) \(j(x)=-4x^2+12x-9 \)
f) \(k(x)=5x^2-45 \)
