Lineare Ungleichungen
Der Übergang von linearen Gleichungen zu Ungleichungen erfolgt durch Ersetzen des Gleichheitszeichens \(=\) durch eines der Ungleichungszeichen
- \(>\) (größer als),
- \(<\) (kleiner als),
- \(\ge\) (größer oder gleich) oder
- \(\le\) (kleiner oder gleich).
Eine lineare Ungleichung wäre also z.B. \(2x-4>4\).
Im Gegensatz zu linearen Gleichungen, bei denen die Lösungsmenge jeweils ein Element enthält (die Schnittstelle der zugehörigen Geraden im Koordinatensystem), besitzen lineare Ungleichungen stets ein ganzes Intervall, in dem die Ungleichung richtig ist.
Im Folgenden sollen zwei Lösungsverfahren für lineare Ungleichungen vorgestellt werden:
Rechnerische Lösung
Rechnerisch werden lineare Ungleichungen sehr ähnlich zu linearen Gleichungen, nämlich durch Äquivalenzumformungen, gelöst. Betrachtet man das Beispiel von oben, so folgt:
\[\begin{array}{rlll}2x-4&>&4 & \vert +4\\2x&>&8&\vert :2\\x&>&4\end{array}\]
Die Ungleichung ist also immer dann erfüllt, wenn die Variable \(x\) größer als 4 ist. Für die Lösungsmenge \(L\) folgt also: \(L=]4;\infty[=\{x\vert x>4\}\).
Aufpassen muss man beim Lösen von linearen Ungleichungen insbesondere dann, wenn man mit negativen Zahlen multipliziert oder durch sie dividiert. In diesem Fall wird das Ungleichheitszeichen umgedreht:
- aus \(>\) wird \(<\)
- aus \(\ge\) wird \(\le\)
und umgekehrt.
\[\begin{array}{rlll}-\frac12 x+4&\ge&16 & \vert -4\\-\frac12 x&\ge&12&\vert \color{red}{\cdot (-2)}\\x&\color{red}{\le}&-24\end{array}\\L=]-\infty;-24]=\{x\vert x\le -24\}\]
Warum ist das so?
Vermeidet man die Multiplikation mit dem negativen Wert, so kann man das früher oder später entstehende \(-x\) „auf die andere Seite addieren“ und die rechte Seite „nach links subtrahieren“.
\[\begin{array}{rlll}-\frac12 x+4&\ge&16 & \vert -4\\-\frac12 x&\ge&12&\vert \color{red}{\cdot 2}\\-x&{\ge}&24 & \vert -24; \vert+x\\-24&{\ge}&x& \\x&\color{red}{\le}&-24\end{array}\\L=]-\infty;-24]=\{x\vert x\le -24\}\]
Zeichnerische Lösung
| Soll die Ungleichung stattdessen zeichnerisch gelöst werden, so bietet es sich an, dass man die rechte Seite der Ungleichung zunächst durch Äquivalenzumformungen auf Null bringt. Aus \(2x-4>4\) wird also durch Subtrahieren von \(4\) auf beiden Seiten \(2x-8>0\).
Diese Ungleichung lässt sich nun in einem Koordinatensystem folgendermaßen interpretieren: für welche \(x\)-Werte verläuft die Gerade mit der Gleichung \(y=2x-8\) oberhalb der Null, also oberhalb der \(x\)-Achse? Zeichnet man die Gerade unter Ausnutzung von Steigung und \(y\)-Achsenabschnitt in ein Koordinatensystem, so erkennt man, dass dies ab \(x=4\) der Fall ist. Folglich ist – wie oben errechnet – die Lösungsmenge erneut \(L=]4;\infty]\). |
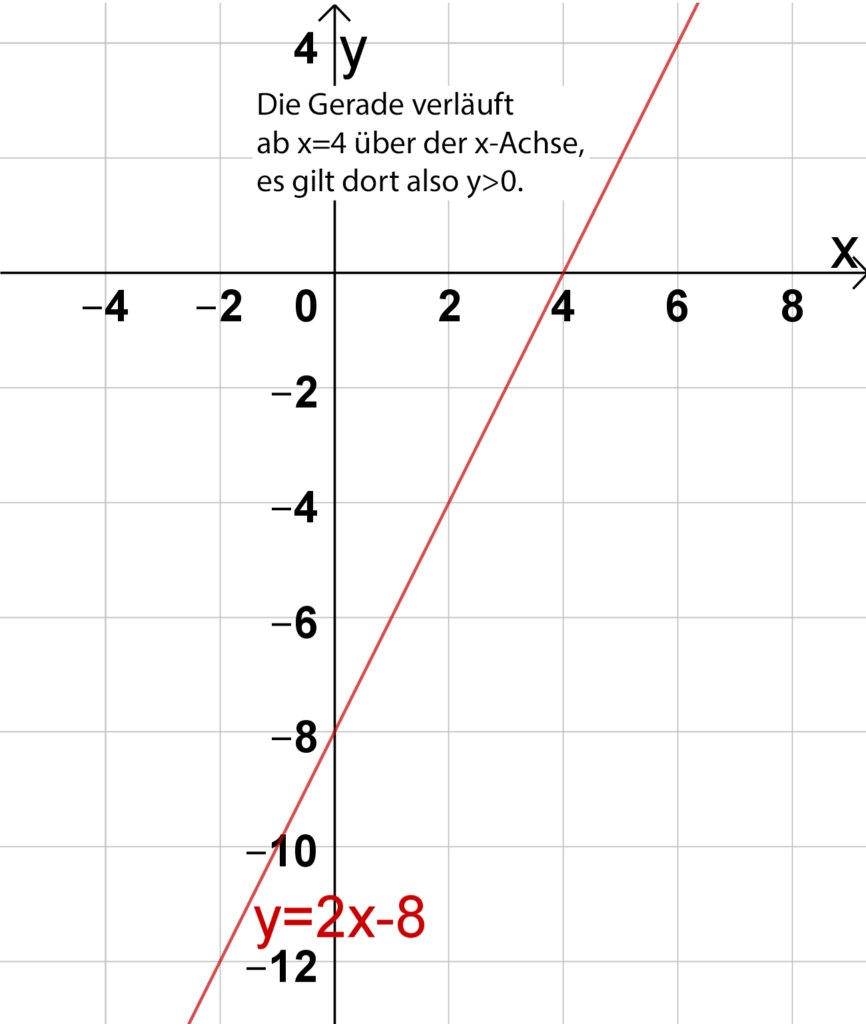 |
Die beiden Lösungsverfahren sind für lineare Ungleichungen gleichermaßen geeignet, um die Lösungsmenge zu bestimmen. Im Laufe des Schuljahres wird das zeichnerische Lösen von Ungleichungen immer wieder auftauchen und kommt bei komplexeren Funktionen fast ausschließlich zum Einsatz.
Aufgabe
Sorgen Sie für die folgenden Ungleichungen zunächst dafür, dass eine Seite \(0\) wird. Bestimmen Sie anschließend jeweils die Lösungsmenge zunächst zeichnerisch und bestätigen Sie danach das Ergebnis rechnerisch.
- \(-2x-1>3\)
- \(\frac34 x+2<-1\)
- \(2x-4\le x-7\)
Komplexe Anwendungsaufgabe
Bei der Wahl eines neuen Handytarifs stehen folgende drei Angebote zur Verfügung:
- Tarif A: All-Net-Flat zum Festpreis von 20€
- Tarif B: Kein monatlicher Grundpreis, 0,10€ pro Verbrauchseinheit
- Tarif C: 10€ Grundpreis mit 150 Inklusiveinheiten, danach 0,08€ pro Verbrauchseinheit
- Stellen Sie die Gesamtkosten der drei Tarife in in Abhängigkeit der monatlich verbrauchten Einheiten in einem gemeinsamen Koordinatensystem dar. Zeichenhinweise:
- Verbrauchseinheiten für \(0\le x \le 300, 1 cm \widehat{=} 20\) Einheiten
- Gesamtkosten: \(0\le y \le 30, 1 cm \widehat{=} 5€\)
- Tarif C besitzt nach den Inklusiveinheiten die Funktionsgleichung \(c(x)=0,08x-2\). Berechnen Sie hiermit den Schnittpunkt \(S\) der Graphen zu den Tarifen A und C.
- Sprechen Sie auf Grundlage der Graphen aus 2.1 und dem Ergebnis aus 2.2 eine Empfehlung für eine Freundin aus, die auf der Suche nach einem neuen Handytarif ist.

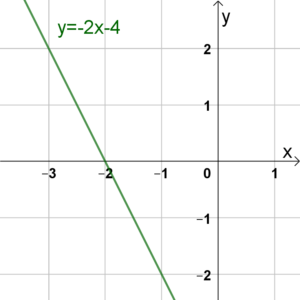 Die Gerade liegt für \(x\in]-\infty;-2[\) oberhalb der \(x\)-Achse.
Die Gerade liegt für \(x\in]-\infty;-2[\) oberhalb der \(x\)-Achse.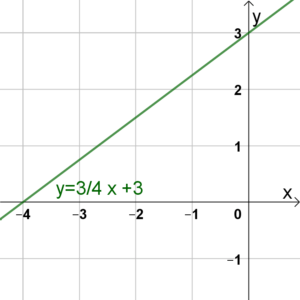 Die Gerade liegt für \(x\in]-\infty;-4[\) unterhalb der \(x\)-Achse.
Die Gerade liegt für \(x\in]-\infty;-4[\) unterhalb der \(x\)-Achse.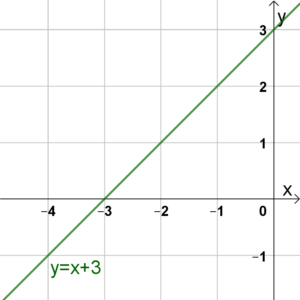 Die Gerade liegt für \(x\in]-\infty;-3]\) unter bzw. auf der \(x\)-Achse.
Die Gerade liegt für \(x\in]-\infty;-3]\) unter bzw. auf der \(x\)-Achse.