Die Ableitung des logischen ER-Modells aus den Vorgaben des semantischen Datenbankmodells
Wie bereits festgestellt, muss ein DBMS nicht „verstehen“, worum es sich z.B. bei einem Schüler oder einer Klasse handelt. Vielmehr muss festgelegt werden, in welchem logischen Zusammenhang die beiden Mengen bzw. deren Datensätze zueinander stehen. So ist – wie bereits festgestellt – unstrittig, dass z.B. eine Klasse eine (un-) bestimmte Anzahl an Schülern haben und ein Schüler zu gleichem Zeitpunkt lediglich einer Klasse zugeordnet sein kann. Wir gehen hier vom klassischen Begriff „Klasse“ aus, also ohne z.B. Wahlpflichtkurse, Sportgruppen, etc. zu beachten.
Diese logische Festlegung muss in einem weiteren Schritt für jede Beziehung des semantischen ER-Modells getroffen werden.
Betrachten wir zunächst die Beziehung zwischen den Relationen „schüler“ und „klasse“:

Semantisches Datenbankmodell, bestehend aus den Relationen „schüler“ und „klasse“
Die Beziehungen zwischen den Elementen „schüler“ und „klasse“ sind in dem semantischen ER-Modell der Bedeutung nach festgelegt.
Vom semantischen Datenbankmodell zum logischen Datenbankmodell durch das Hinzufügen von Kardinalitäten
Wir überlegen, wie wir die fehlenden Informationen über die logischen Zusammenhänge zwischen den Elementen in der Relation „schüler“ und denen der Relation „klasse“ dem semantischen ER-Modell hinzufügen können. Ein mögliches Ergebnis könnte wie folgt aussehen:

Logisches Datenbankmodell, bestehend aus den Relationen „schüler“ und „klasse“
Das semantische ER-Modell wurde um zwei Informationen in Form der Zeichen „n“ und „1“ ergänzt. Diese Symbole werden im Zusammenhang mit der Erstellung von Datenbanken Kardinalitäten genannt.
Interpretiert ergibt das: Jeder Schüler kann genau einer Klasse zugeordnet werden. Eine Klasse kann wiederum mehrere Schüler enthalten.
Wichtig für diese Interpretationen ist die Erkenntnis, dass jede Beziehung zwischen zwei Relationen in zwei Richtungen interpretiert werden kann.
Jede dieser Interpretationsrichtungen nennt man Assoziation, womit folgt, dass eine Beziehung grundsätzlich aus zwei Assoziationen besteht. Zum Zweck der Unterscheidung benennt man die eine Assoziation mit „a“, die jeweils entgegengesetzte mit „a*“.
Damit ergibt sich folgende Schreibweise:
– Die Assoziation von „schüler“ zu „klasse“ wird geschrieben als: a(s,k)
– In Gegenrichtung wird die Assoziation wie folgt geschrieben: a*(k,s)
Um nun die Kardinalitäten bestimmen zu können, bedient man sich des folgenden Prüfschemas:
Wir behandeln zunächst die Assoziation a:
| Frage | Antwort | |
| In Worten | Wieviele Elemente der Relation „klasse“ können einem Element der Relation „schüler“ zugeordnet werden? | Einem Schüler kann genau eine Klasse zugeordnet werden. |
| Symbolik | a (s ; k) ….1 ? |
a (s ; k) ….1 1 |
Wenden wir uns jetzt der Assoziation a* zu
| Frage | Antwort | |
| In Worten | Wieviele Elemente der Relation „schüler“ können einem Element der Relation „klasse“ zugeordnet werden? | Einer Klasse können mehrere Schüler zugeordnet werden. |
| Symbolik | a* (k ; s) ……1 ? |
a* (k ; s) ……1 n |
Wie die Kardinalitäten der beiden Fragestellungen in das semantische Modell eingefügt werden, haben wir oben bereits vorweg genommen.
Als Ergebnis erhalten wir eine sog. 1:n-Beziehung, in welcher jedem Element der einen Menge (schüler) genau ein Element der anderen Menge (klasse) zugeordnet ist.
Dies lässt den logischen Rückschluss zu, dass ein Schüler, welcher in einer bestimmten Klasse ist, keiner anderen Klasse zugeordnet sein kann. Umgekehrt ist dieser logische Rückschluss nicht möglich: Aus der Tatsache, dass ein bestimmter Schüler in einer Klasse ist, lässt sich nicht schließen, dass (k)ein anderer bestimmter Schüler in dieser Klassen (nicht) ist.
Damit das DBMS mit der Beziehung umgehen kann, ist der logische Rückschluss in einer der beiden Assoziationen zwingend notwendig. Er ist eine unabdingbare Voraussetzung dafür, dass die Beziehung später mit Hilfe eines geeigneten Programms in digitaler Form implementiert werden kann.

Semantisches Datenbankmodell, bestehend aus den Relationen „klasse“ und „lehrkraft“:
Auch hier wenden wir das soeben kennen gelernte Prüfschema an:
Wir betrachten zunächst die Assoziation a:
| Frage | Antwort | |
| In Worten | Wieviele Elemente der Relation „lehrkraft“ können einem Element der Relation „klasse“ zugeordnet werden? | Einer Klasse können mehrere Lehrkräfte zugeordnet werden. |
| Symbolik | a (k ; l) ….1 ? |
a (k ; l) ….1 n |
Jetzt widmen wir unser Augenmerk der Assoziation a*:
| Frage | Antwort | |
| In Worten | Wieviele Elemente der Relation „klasse“ können einem Element der Relation „lehrkraft“ zugeordnet werden? | Einer Lehrkraft können mehrere Klassen zugeordnet werden. |
| Symbolik | a* (l ; k) …..1 ? |
a* (l ; k) …..1 m |

Logisches Datenbankmodell, bestehend aus den Relationen „klasse“ und „lehrkraft“
Als Ergebnis erhalten wir eine sog. n:m-Beziehung, wobei die Buchstaben n und m für eine jeweils unterschiedliche, theoretisch unbegrenzte Anzahl stehen. Die unterschiedlichen Buchstaben werden verwendet, um das Missverständnis zu umgehen, dass in beiden Fällen gleiche Werte auftreten müssten.
Wir halten fest:
- Um die logischen Beziehungen zwischen den Elementen zweier Relationen zueinander festzulegen, ergänzt man das semantische ER-Modell um sog. Kardinalitäten.
- Die Kardinalitäten können die Werte 1, n und m annehmen, wobei n und m gleichbedeutend sind.
- Welche Werte zur Anwendung kommen, wird für jede Beziehung mittels Prüfschema ermittelt.
- Zu diesem Zweck unterscheidet man pro Beziehung zwei Assoziationen, welche für die beiden Lese- bzw. Interpretationsrichtungen einer Beziehung stehen: a und a*
- Wichtig hierbei ist, dass eine der beiden Assoziationen einer Beziehung eindeutig ist, d.h. einen logischen Rückschluss zulässt: Wenn ein Schüler in einer Klasse ist, so kann er nicht in einer anderen Klasse sein.
Die Problematik der n:m-Beziehung: In diesem Fall lässt keine Interpretationsrichtung – Assoziation – einen logischen Rückschluss zu: Weder lässt sich aus der Tatsache, dass in einer Klasse eine bestimmte Lehrkraft unterrichtet, diese in (k)einer anderen Klasse unterrichtet. Das betrifft a. Noch lässt diese Tatsache den Rückschluss in a* zu, dass daraus abzuleiten ist, dass (k)eine andere Lehrkraft in eben dieser Klasse unterrichtet. Somit besteht weder für a noch für a* die Möglichkeit eines logischen Rückschlusses und damit keine Eindeutigkeit.
Das folgende Video fasst die Schritte vom semantischen zum logischen Datenbankmodell noch einmal zusammen:
Aufgaben:
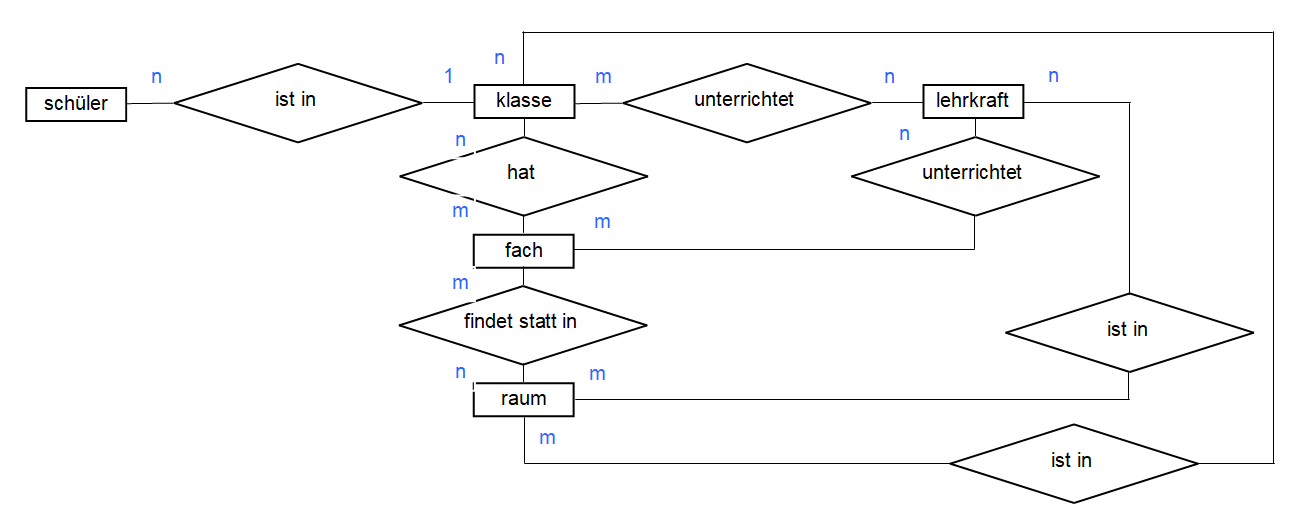
1 Ergänzen Sie die übrigen Beziehungen unseres semantischen Datenbankmodells einer Schule um die fehlenden Kardinalitäten. Wenden Sie hierbei konsequent das Prüfschema an. Schreiben Sie die Prüfschemata auf.
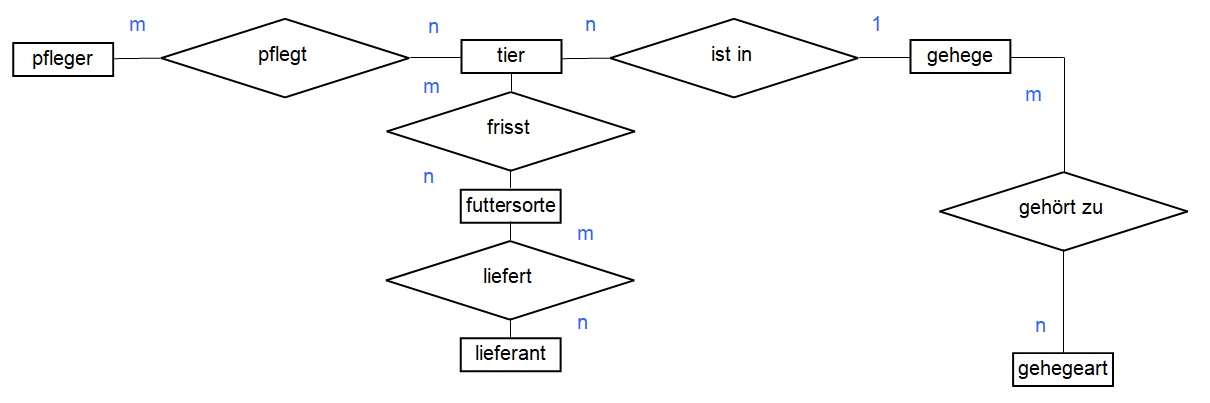
2 Überführen Sie das semantische Datenbankmodell des Tiergartens in ein logisches Datenbankmodell, indem Sie für jede Beziehung das Prüfschema anwenden. Führen Sie auch hier die Prüfungen handschriftlich durch.
Lösungen
Auf der aktuellen Seite haben wir uns mit der Ableitung des logischen ER-Modells aus dem semantischen ER-Modell beschäftigt. Das Ergebnis waren die Beziehungstypen 1:n und n:m. Auf der folgenden Seite wollen wir uns mit den einzelnen Beziehungstypen und den damit verbundenen Problemen widmen.