Die verschiedenen Beziehungstypen in einem ER-Modell und die daraus resultierenden Abbildungsregeln
Im voran gegangenen Kapitel lernten wir das ER-Modell samt seiner Bestandteile Rechteck, Raute und Kardinalität kennen. Es ist uns jetzt möglich, den jeweiligen Beziehungstyp festzustellen. In diesem Zusammenhang machten wir die Bekanntschaft von 1:n– und n:m-Beziehungen.
Auf den folgenden Seiten geht es darum, die verschiedenen Beziehungstypen näher zu betrachten. Nicht alle Beziehungstypen sind dazu geeignet, direkt mit Hilfe des DBMS in den PC eingegeben zu werden.
Wir werden in diesem Kapitel folgenden Fragen nachgehen:
- Welche Rolle spielt die Eindeutigkeit bei Beziehungen für die spätere Anwendung einer Datenbank?
- Wie kann die Eindeutigkeit im Nachhinein hergestellt werden?
- Welche Beziehungstypen bzw. –arten gibt es grundsätzlich?
Da wir, um die folgenden Probleme zu lösen, auf die Darstellung der einzelnen Relationen mit deren Inhalten zugreifen müssen, soll an dieser Stelle bereits eine Konvention eingeführt werden, die wir ab sofort strikt einhalten werden: alle Relationen bekommen das Präfix „tbl_“. Damit ist gewährleistet, dass wir Relationen im DBMS eindeutig von Abfragen („qry_“) und Formularen („frm_“) unterscheiden können.
Warum ist die Eindeutigkeit als Bedingung für den logischen Rückschluss so wichtig für die Umsetzung des Datenbankkonzeptes in einem DBMS?
Um der gestellten Frage auf den Grund zu gehen, ist es erforderlich, sich zunächst eine 1:n-Beziehung zwischen zwei Tabellen mit deren jeweiligen Inhalten anzusehen, wobei wir uns jetzt schon auf die Darstellung der Datenbank als relationales Modell nähern:
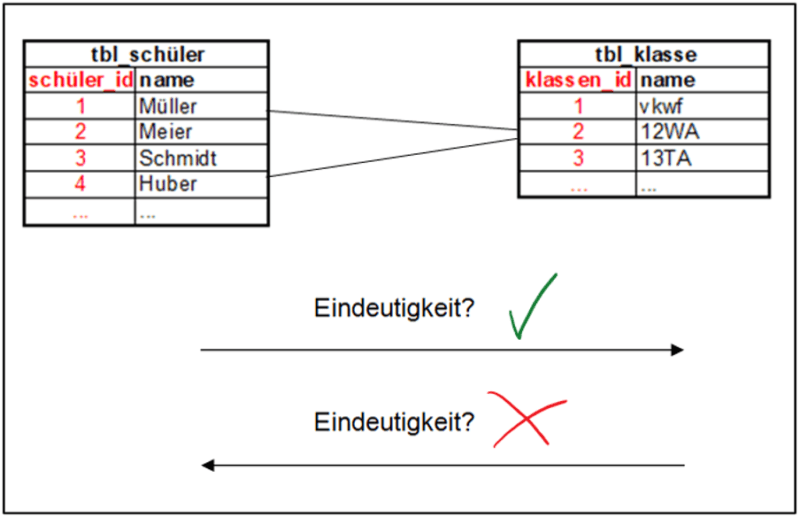
1:n-Beziehung zwischen tbl_schüler und tbl_klasse mit Betrachtung der Eindeutigkeit
Während die Beziehung zwischen Schüler und Klasse von links nach rechts (Assoziation a) eindeutig ist und damit einen logischen Rückschluss zulässt, ist dies von rechts nach links (a*) nicht der Fall: Weil Schüler Müller in der 12WA ist, kann nicht auf andere Schüler rückgeschlossen werden, die (nicht) in der Klasse sind.
Betrachten wir die n:m-Beziehung zwischen Klasse und Fach:
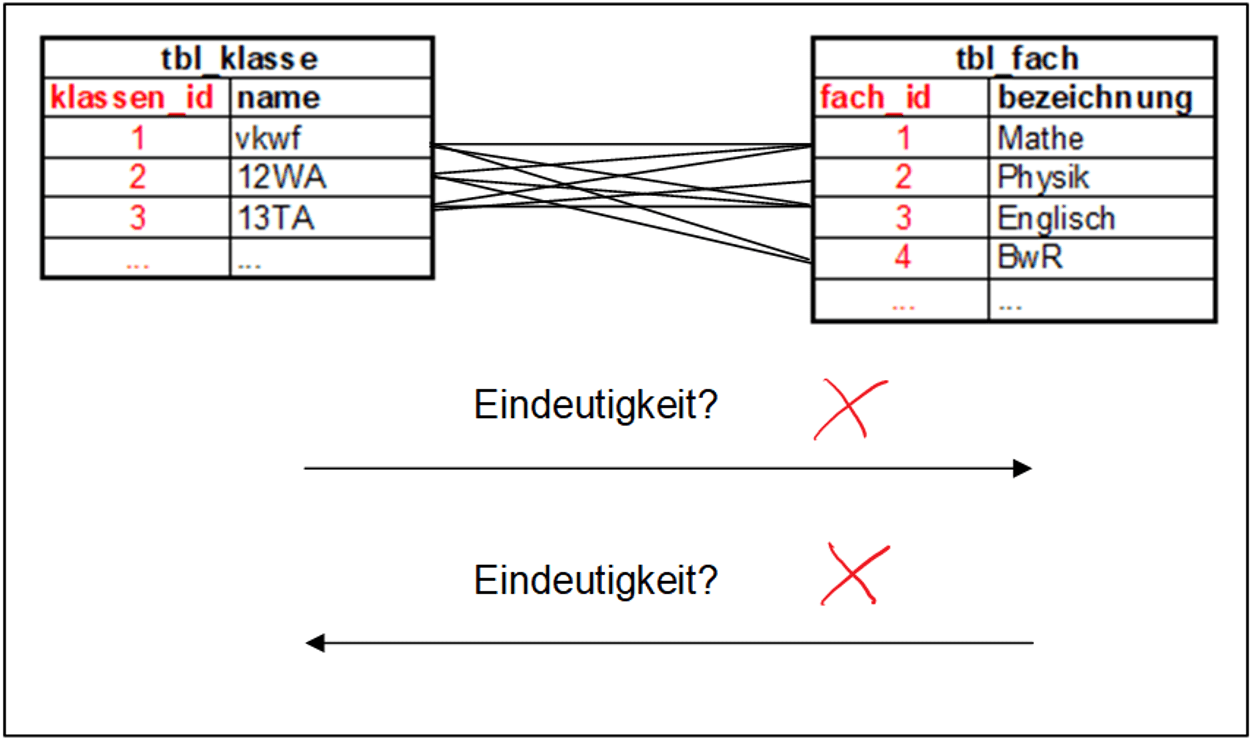
n:m-Beziehung zwischen tbl_klasse und tbl_fach mit Betrachtung der Eindeutigkeit
Keine Assoziation, weder a noch a*, ist eindeutig und lässt somit keinen logischen Rückschluss zu, weswegen die Beziehung in dieser Form nicht digital umgesetzt werden kann.
Wie lässt sich die n:m-Beziehung so umwandeln, dass sie digital umgesetzt werden kann?
Um zu verstehen, wie die Umwandlung einer n:m-Beziehung in mehrere 1:m bzw. n:1-Behiehungen erfolgt, müssen wir einen Blick in die (fiktiven) Datensätze der durch eine n:m-Beziehung miteinander verbundenen Relationen werfen. Wir tun das anhand der Relationen für die Klassen sowie für die Fächer.
An dieser Stelle soll sogleich darauf aufmerksam gemacht werden, dass jede Relation in einer Datenbank eindeutig benannt sein muss und alle Relationen das Pfäfix „tbl_“ (tbl steht für das englische Wort für Tabelle: table) erhalten. So sind sie in doppelter Hinsicht identifizierbar: ihr Name ist eindeutig und weist auf den Inhalt hin. Durch das Präfix sind sie als Relation erkennbar.
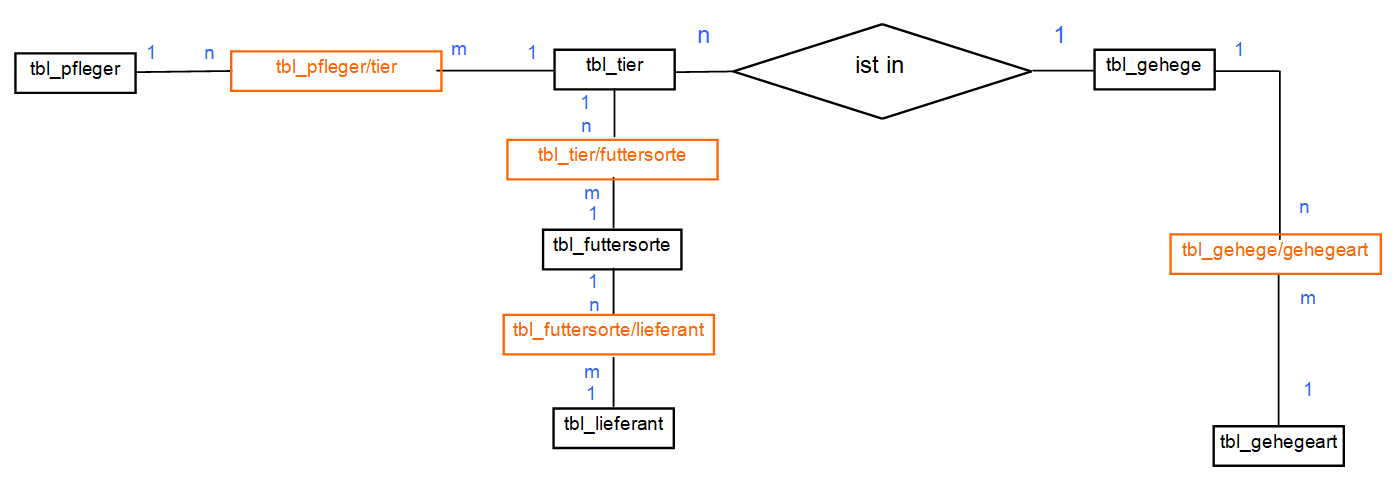
Sehen wir uns nun Ergebnis der Umwandlung einer n:m-Beziehung näher an:
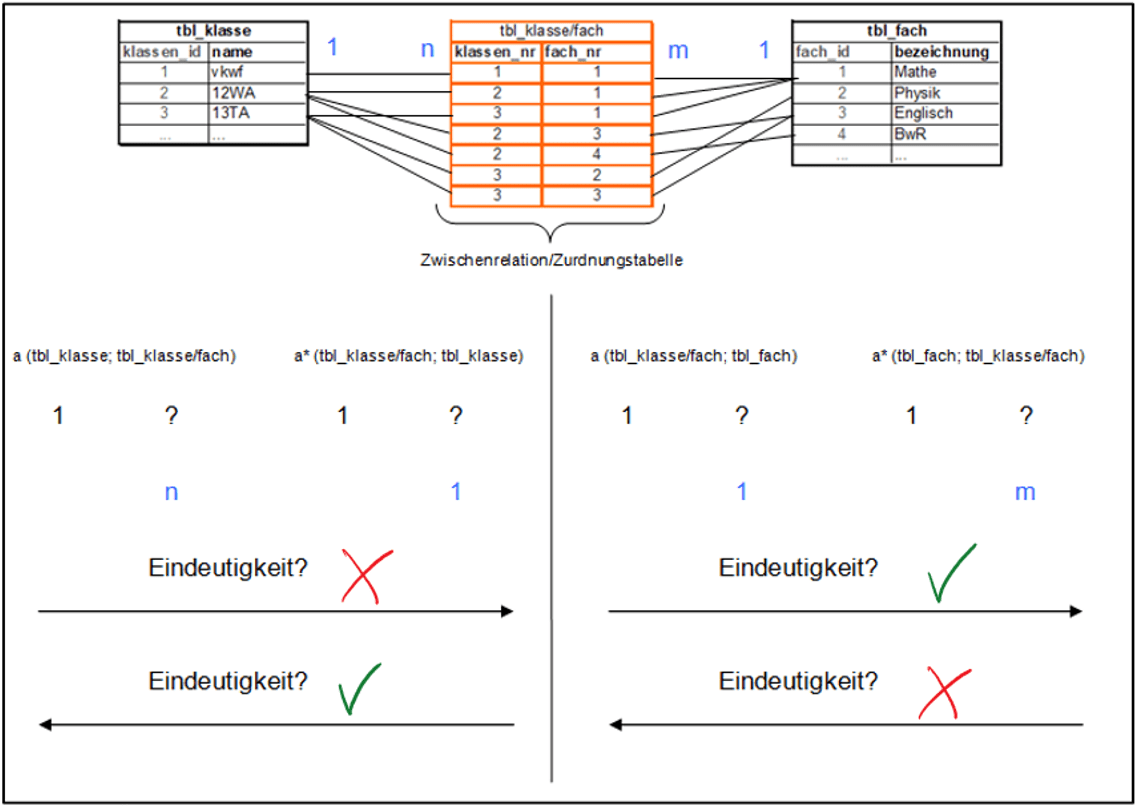
Auswirkungen des Einfügens einer sog. Zwischenrelation (Zuordnungstabelle) auf die Eindeutigkeit der Beziehungen bzw. Assoziationen
Es wird eine sog. Zwischenrelation oder Zuordnungstabelle „tbl_klasse/fach“ zwischen die beiden ursprünglichen Relationen „tbl_klasse“ und „tbl_fach“ eingefügt. Sie nimmt alle Paarungen auf. (Um nachträglich feststellen zu können, welche Relation im Nachhinein eingefügt wurde, verzichtet man bei den neu entstandenen Beziehungen im ER-Modell auf die Rauten.) Die Bezeichnung der neuen Relation setzt sich in aller Regel aus den Bezeichnungen der ursprünglichen Relationen, getrennt durch einen Schrägstrich (slash), und dem Präfix „tbl_“ zusammen.
Prüft man die beiden durch das Einfügen der Zwischenrelation neu entstandenen Beziehungen, so erhält man zwei 1:n- bzw. m:1-Beziehungen.
Wir halten fest:
- Eine n:m-Beziehung lässt sich durch Einfügen einer dritten Relation in zwei 1:n-Beziehungen (1:n und m:1) auflösen.
- Jeweils eine Assoziation der beiden daraus entstehenden Beziehungen ist eindeutig und lässt einen logischen Rückschluss zu.
- Die durch den Umwandlungprozess entstandenen Relationen werden Zwischenrelationen (oder Zuordnungstabellen) genannt. Sie erhalten die Bezeichnung „tbl_relation1/relation2“.
Welche Arten von Beziehungen (Abbildungsregeln) gibt es grundsätzlich?
Die unterschiedlichen Beziehungstypen werden unter dem Sammelbegriff „Abbildungsregeln“ zusammengefasst:
- Abbildungsregel 2: einfach-komplexe Beziehungen (1:n-Beziehung)
z.B. Schüler-Klasse - Abbildungsregel 3: komplex-komplexe Beziehungen (n:m-Beziehung)
z.B. Klasse-Fach, Fach-Lehrer, Lehrer-Klasse;
Wenn Sie die Aufzählung aufmerksam gelesen haben, so fällt Ihnen auf, dass die Abbildungsregel 1 (noch) fehlt:
- Abbildungsregel 1: einfach-einfache Beziehungen (1:1-Beziehung)
Hierunter würde z.B. eine Beziehung zwischen der Tabelle der Lehrer und der (fiktiven) Tabelle der Personalnummern fallen: Jeder Lehrer hat genau eine Personalnummer. Jede Personalnummer ist genau einem Lehrer zugeordnet. Bei längerem Überlegen kommt man jedoch darauf, dass es einfacher und damit auch sinnvoller ist, das Attribut „Personalnummer“ in die Tabelle Lehrer aufzunehmen. Grundsätzlich lässt sich über 1:1-Beziehungen sagen, dass sie in den meisten Fällen überflüssig sind.
Aufgaben:
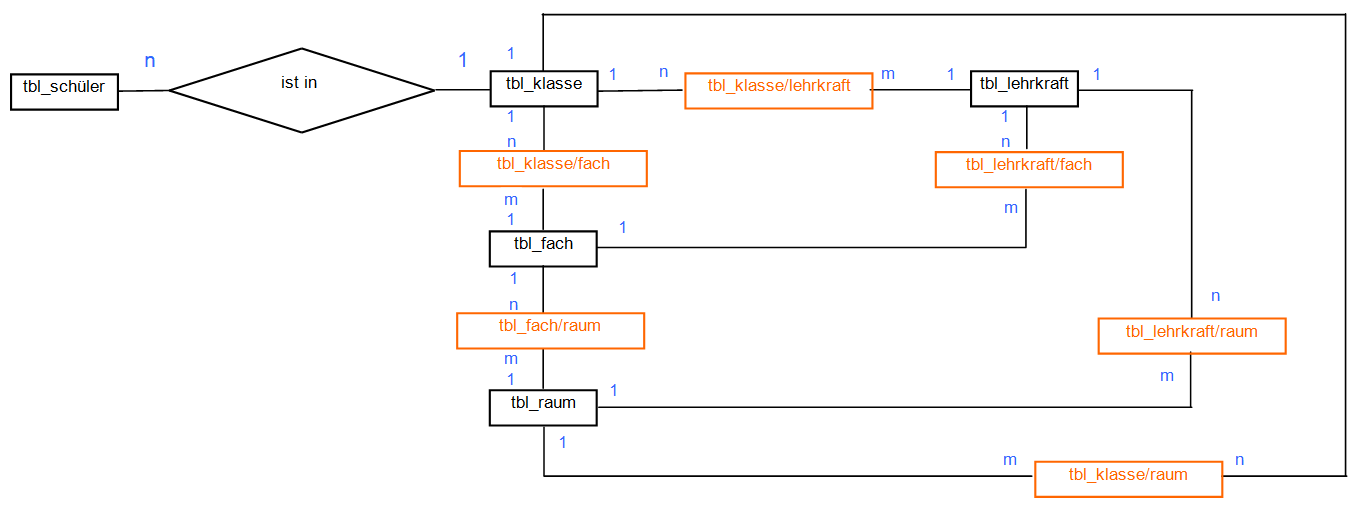
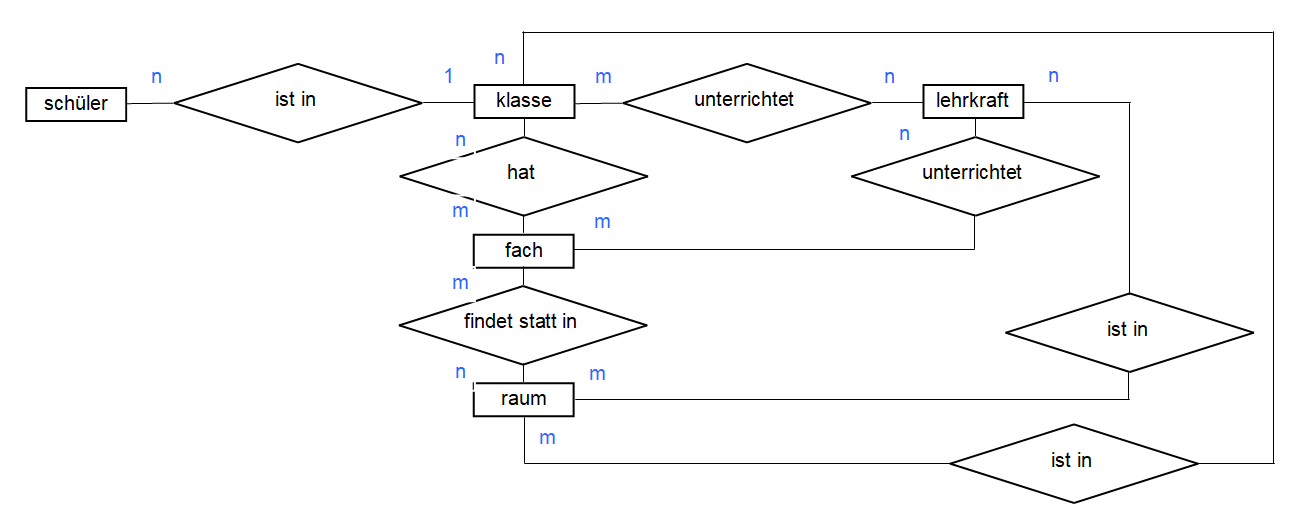
1 Nehmen Sie auch jetzt wieder Papier und Bleistift zur Hand. Lösen Sie alle n:m-Beziehungen des logischen ER-Modells „Schule“ auf. Zur Erinnerung sehen Sie das Modell hier noch einmal abgebildet:
Logisches ER-Modell „Schule“
Aufgaben:
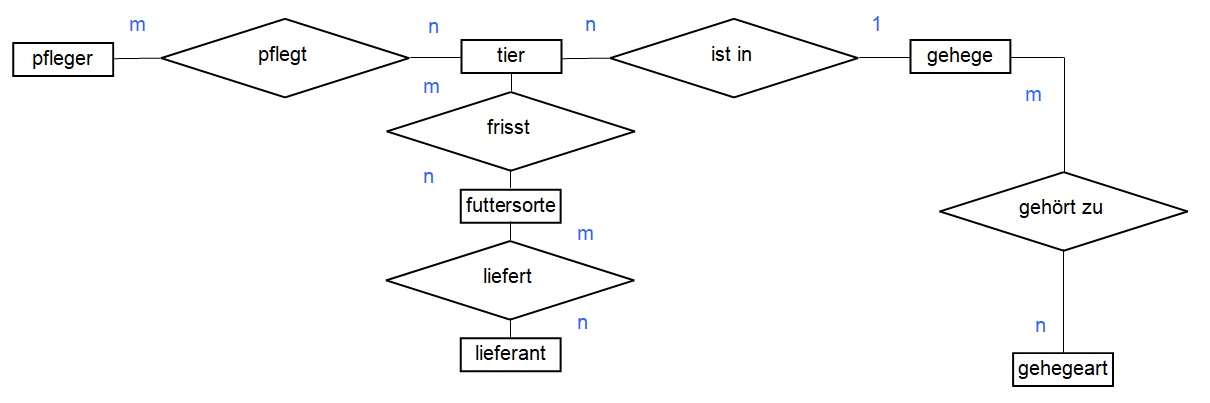
2 Nehmen Sie auch jetzt wieder Papier und Bleistift zur Hand. Lösen Sie alle n:m-Beziehungen des logischen ER-Modells „Tiergarten“ auf. Zur Erinnerung sehen Sie das Modell hier noch einmal abgebildet::
Logisches ER-Modell „Tiergarten“