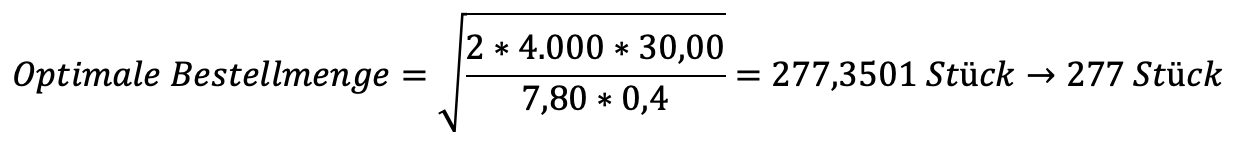Optimale Bestellmenge
Lagerkosten und Bestellkosten
Für Unternehmen stellt sich die Frage, wie häufig Rohstoffe für die Produktion oder auch Büromaterial für die Verwaltung bestellt werden soll. Bestellt man sehr häufig, so bedeutet das eine geringe Bestellmenge und damit einen geringen Lagerbestand. Die Kosten für die Bestellungen steigen jedoch an.
Bestellt man sehr große Mengen muss der Bestellvorgang nicht so häufig durchgeführt werden und die Kosten dafür sind gering. Die Lagerbestände sind jedoch sehr hoch und verursachen hohe Kosten.
Bestellkosten sind zum Beispiel:
· Bearbeitung der Bedarfsmeldung
· Angebotseinholung
· Wareneingangsprüfung
· Rechnungsprüfung
· Porto
· Kontrolle
· Ablage
· Buchung
· Zahlungsvorgang
Der grafische Verlauf der Bestellkosten hängt davon ab, welchen Wert man auf die X-Achse schreibt:
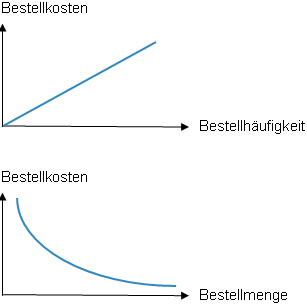
Je häufiger bestellt wird, umso höher sind die Bestellkosten.
Die Bestellkosten sind hoch, wenn die Bestellmenge gering ist und dadurch häufig bestellt werden muss.
Die Lagerkosten entstehen hauptsächlich dadurch, dass eine hohe Kapitalbindung entsteht. Es werden kalkulatorische Zinskosten oder auch Kosten pro Stück für die durchschnittlich im Lager gebundene Ware in der Kosten- und Leistungsrechnung ermittelt und in die Kalkulation eingebunden.
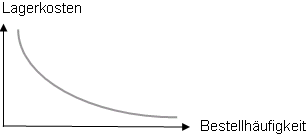
Die Lagerkosten sind hoch, wenn die Bestellhäufigkeit gering und damit die Bestellmenge hoch ist. Wird häufiger bestellt sinken die Lagerkosten degressiv, weil die Bestellmenge und damit das im Lager gebundene Kapital sinkt.
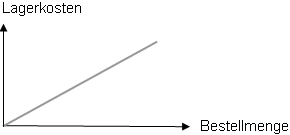
Betrachtet man die Lagerkosten im Zusammenhang mit der Bestellmenge, so steigen diese linear an, wenn die Bestellmenge steigt.
Gesamtkosten
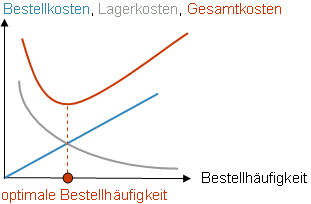
Die Gesamtkosten ergeben sich aus der Addition von Bestellkosten und Lagerkosten. Sie verlaufen parabelförmig. Das Minimum der Gesamtkosten liegt in der doppelten Höhe über dem Schnittpunkt von Lagerkosten und Bestellkosten. Je nach der Art der grafischen Darstellung erhält man entweder die optimale Bestellhäufigkeit auf der X-Achse oder die optimale Bestellmenge.
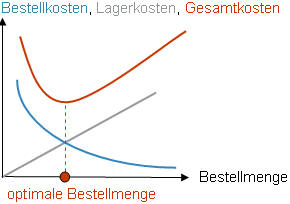
Beispiel 1
Die BOS AG hat für ein Material einen Bedarf von 2.500 Stück pro Jahr. Ein Bestellvorgang wird mit 50,00 € kalkuliert. Die Lagerkosten betragen 0,50 € pro Stück. Ermitteln Sie die optimale Bestellhäufigkeit.
| Bestellhäufigkeit | Bestellmenge | Lagerkosten | Bestellkosten | Gesamtkosten |
| 0 | – | – | – | – |
| 1 | 2.500 | 625,00 € | 50,00 € | 675,00 € |
| 2 | 1.250 | 312,50 € | 100,00 € | 412.50 € |
| 3 | 833 | 208,25 € | 150,00 € | 358,33 € |
| 4 | 625 | 156,25 € | 200,00 € | 356,25 € |
| 5 | 500 | 125,00 € | 250,00 € | 375,00 € |
| 6 | 417 | 104,17 € | 300,00 € | 404,17 € |
| 7 | 357 | 89,29 € | 350,00 € | 439,29 € |
| 8 | 313 | 78,13 € | 400,00 € | 478,13 € |
| 9 | 278 | 69,44 € | 450,00 € | 519,44 € |
Die Lagerkosten werden vom durchschnittlich gebundenen Kapital berechnet. Für die Bestellhäufigkeit von ein mal pro Jahr ergibt sich eine Bestellmenge von 2.500 Stück pro Bestellung. Durchschnittlich sind für ein Jahr dann 1.250 Stück auf Lager. Jedes Stück wird mit 0,50 € angesetzt. Das ergibt 625,00 € Lagerkosten.
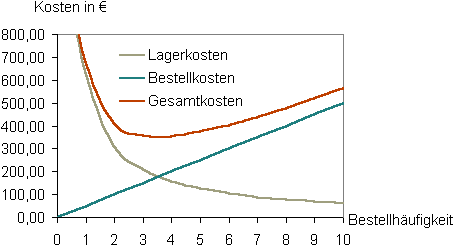
Die optimale Bestellhäufigkeit liegt zwischen drei und vier Mal pro Jahr. Dort ergibt sich ein Minimum an Gesamtkosten.
Beispiel 2
Für ein Fremdbauteil mit einem Jahresbedarf von 288.000 Stück und einem Bezugspreis von 5,00 € fallen pro Bestellvorgang 130,00 € Kosten an. Der Lagerhaltungskostensatz beträgt 15 %. Ermitteln Sie die optimale Bestellmenge.
| Bestell- menge |
Häufigkeit | Bestellkosten in € | Durchschnittlicher Lagerbestand in St. |
Durchschnittlicher Lagerbestand in € |
Lagerkosten in € |
Gesamtkosten in € |
| 10.400 | 27,69 | 3.600,00 | 5.200 | 26.000 | 3.900,00 | 7.500,00 |
| 10.300 | 27,96 | 3.634,95 | 5.150 | 25.750 | 3.862,50 | 7.497,45 |
| 10.200 | 28,24 | 3.670,59 | 5.100 | 25.500 | 3.825,00 | 7.495,59 |
| 10.100 | 28,51 | 3.706,93 | 5.050 | 25.250 | 3.787,50 | 7.494,43 |
| 10.000 | 28,80 | 3.744,00 | 5.000 | 25.000 | 3.750,00 | 7.494,00 |
| 9.900 | 29,09 | 3.781,82 | 4.950 | 24.750 | 3.712,50 | 7.494,32 |
| 9.800 | 29,39 | 3.820,41 | 4.900 | 24.500 | 3.675,00 | 7.495,41 |
| 9.700 | 29,69 | 3.859,79 | 4.850 | 24.250 | 3.637,50 | 7.497,29 |
| 9.600 | 30,00 | 3.900,00 | 4.800 | 24.000 | 3.600,00 | 7.500,00 |
Das Minimum der Gesamtkosten liegt in dieser Berechnung bei 7.494,00 €. Die optimale Bestellmenge beträgt 10.000 Stück. Die Bestellmenge wurde in Schritten zu 100 Stück berechnet. Es ist also nur ein näherungsweises Ergebnis. Mit Hilfe der ANDLER-Formel kann man die genaue Bestellmenge ermitteln:
Grafische Darstellung:
Optimale Bestellmenge: Aufgaben
Testen Sie Ihr Wissen an folgenden Beispielen:
Aufgaben:
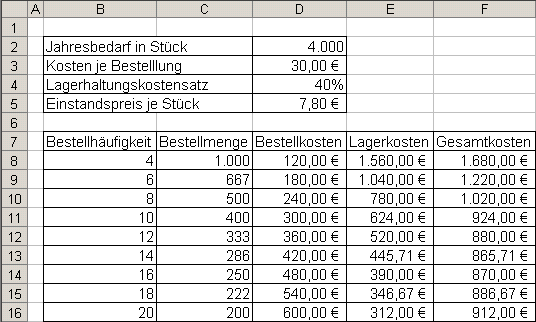
1 In einem Unternehmen besteht für einen Rohstoff ein Jahresbedarf von 4.000 Stück. Die Kosten je Bestellung betragen 30,00 €. Man kalkuliert mit einem Lagerhaltungskostensatz von 40 %. Der Einstandspreis je Stück beträgt 7,80 €.
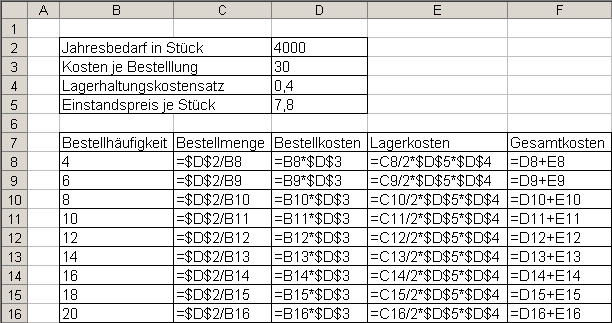
1.1 Ermitteln Sie die optimale Bestellhäufigkeit und die optimale Bestellmenge rechnerisch mit Hilfe der Tabellenkalkulation.
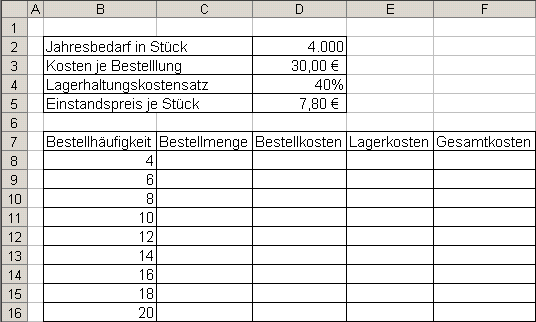
1.2 Ermitteln Sie die optimale Bestellmenge mit Hilfe der ANDLER-Formel.
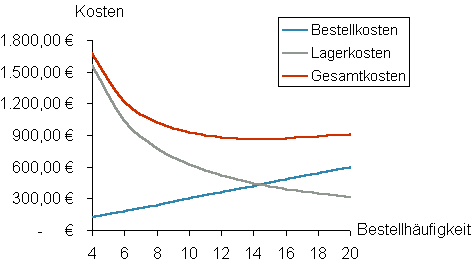
1.3 Stellen Sie die Situation grafisch dar. (Abzisse: Bestellhäufigkeit)
2 Die BOS AG erstellte eine unvollständige Grafik zur Ermittlung der optimalen Bestellmenge.
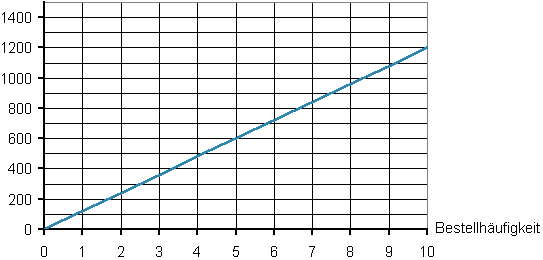
Die optimale Bestellhäufigkeit liegt bei drei. Dies entspricht Lagerkosten von 360,00 €. Bei einer Bestellhäufigkeit von fünf entstehen Gesamtkosten von 816,00 €. Ein Bauteil kostet 72,00 €. Die BOS AG rechnet mit einem Lagerhaltungskostensatz von 10 % vom durchschnittlichen Lagerbestand.
2.1 Ermitteln Sie die Kosten pro Bestellvorgang.
2.2 Nennen Sie zwei Komponenten der Bestellkosten.
2.3 Bestimmen Sie rechnerisch die minimalen Gesamtkosten.
2.4 Ermitteln Sie die Bestellmenge bei einer Bestellhäufigkeit von fünf.
2.5 Ermitteln Sie den Jahresbedarf.
3 Der Einkaufspreis eines Bauteils beträgt 16,00 € pro Stück. Zusätzlich verlangt der Lieferant eine Pauschale von 650,00 €. Die Zins- und Lagerkosten betragen jährlich 9,5 %. Der Jahresbedarf an Bauteilen beträgt 25.000 Stück.
Ermitteln Sie unter Angabe des Rechenweges die optimale Bestellhäufigkeit.
Rechnen Sie für folgende Bestellmengen: 6.250 Stück, 5.000 Stück, 3.125 Stück.
Lösungen
Die optimale Bestellhäufigkeit beträgt 14 mal. Dazu müssen 286 Stück pro Bestellung
geordert werden.
Die Gerade stellt die Bestellkosten dar. 1.200,00 € : 10 = 120,00 €
Zum Beispiel: Kosten der Wareneingangsprüfung, Kosten der Buchhaltung
2 · 360,00 € = 720,00 €
Gesamtkosten 816,00 €
– Bestellkosten 600,00 €
=Lagerkosten 216,00 €
Lagerkosten = Bestellmenge : 2 · Wert pro Stück · Lagerhaltungskostensatz
216,00 € = Bestellmenge : 2 · 72 €/St. · 10 %
Bestellmenge = 60 Stück
Jahresbedarf = Bestellmenge · Bestellhäufigkeit
Jahresbedarf = 60 Stück · 5 = 300 Stück
| Bestellmenge | Bestellhäufigkeit | Bestellkosten | Lagerkosten | Gesamtkosten | |
| 25.000 : BM | B.-Hfgk. · 650 € | BM : 2 · 9,5 % · 16,00€ | BK + LK | ||
| 3.125 | 8 | 5.200,00 € | 2.375,00 € | 7.575,00 € | |
| 5.000 | 5 | 3.250,00 € | 3.800,00 € | 7.050,00 € | |
| 6.250 | 4 | 2.600,00 € | 4.750,00 € | 7.350,00 € |