Statische Investitionsrechenverfahren
Erweiterung der Situation:
Im Rahmen der Erweiterung der E-Bike-Produktion benötigt die FAHRRADWELT AG eine neue Produktionsanlage. Sie sind Mitarbeiter in der Finanzbuchhaltung und sollen mithilfe statischer Investitionsrechenverfahren zwei vorliegende Investitionsalternativen beurteilen. Das Unternehmen kalkuliert mit einem Zinssatz von 5 % p.a.
| Produktionsanlage I | Produktionsanlage II | |
| Anschaffungskosten | 260.000,00 € | 210.000,00 € |
| Preisindex (bezogen auf Nutzungsdauer) | 105,00 | 105,00 |
| wirtschaftliche Nutzungsdauer | 10 | 10 |
| Kapazität pro Jahr | 20.000 Stück | 19.500 Stück |
| sonstige fixe Kosten pro Jahr | 17.000,00 € | 25.000,00 € |
| variable Kosten pro Stück | 25,10 € | 19,50 € |
Statische Investitionsrechenverfahren
Steht ein Unternehmen vor der Wahl zu investieren, kommt es sehr häufig dazu, dass es sich zwischen mehreren Investitionsalternativen entscheiden muss. Hier können statische Investitionsrechenverfahren eine Hilfe sein. Der Faktor Zeit wird hier außer Acht gelassen. Aus diesem Grund spricht man von statischen Verfahren. Unter diesen Verfahren werden gleich mehrere Berechnungen zusammengefasst:
(1) Kostenvergleichsrechnung
(2) Gewinnvergleichsrechnung
(3) Rentabilitätsrechnung
(4) Amortisationsrechnung
Auf diese Verfahren wird nun im Einzelnen eingegangen.
(1) Kostenvergleichsrechnung
Steht man vor der Entscheidung, zwischen zwei Investitionsalternativen zu wählen oder aber z.B. eine alte Maschine durch eine neue zu ersetzen, kann die Kostenvergleichsrechnung helfen. Hier werden die Gesamtkosten von zwei oder mehreren Anlagen bzw. die Gesamtkosten der alten Anlage und der neuen Anlage verglichen. Ein Stückkostenvergleich ist dann notwendig, wenn die Anlagen unterschiedliche Kapazitäten aufweisen. Es ist aber auch möglich, die Kosten auf den Beschäftigungsgrad oder die Stunden zu beziehen. Bei z.B. einer schwankenden Kapazitätsauslastung schließt der Vergleich die kritische Menge bzw. den kritischen Ersatzzeitpunkt mit ein. Im Fokus der Kostenvergleichsrechnung stehen die Kosten, Erlöse werden nicht miteinbezogen.
Die Kostenvergleichsrechnung ist einfach durchzuführen, und kann bei kleineren Investitionen z.B. Kopierer angewendet werden. Folgender Nachteil ergibt sich aus der angesprochenen Einfachheit: Es wird lediglich die Kostenseite der Investitionen überprüft. Erlöse oder der Gewinn werden gänzlich außen vor gelassen. Dies ist nur dann sinnvoll, wenn unterstellt werden kann, dass identische Erlöse mit den Investitionsalternativen einhergehen.
Die Kostenvergleichsrechnung berücksichtigt alle mit der Investition einhergehenden fixen und variablen Kosten sowie die kalkulatorischen Kosten. Die Anschaffungskosten gehen nur indirekt über die kalkulatorischen Zinsen und kalkulatorischen Aschreibungen mit ein.
Die Berechnung der kalkulatorischen Zinsen erfolgt in der Regel vom durchschnittlich gebundenen Kapital. Da zu Beginn der Nutzung alle Anschaffungskosten gebunden sind, zum Ende der Nutzung allerdings das gesamte investierte Kapital seinen Weg zurück über die Abschreibung findet, werden nur die halben (durchschnittlichen) Anschaffungskosten berücksichtigt. Der kalkulatorische Zinssatz kann bspw. der Zins für Fremdkapital sein. Es ist aber auch durchaus möglich, einen höheren Kalkulationszinssatz (z.B. Berücksichtigung eines Risikozuschlags) anzusetzen. Die Berechnung erfolgt folgendermaßen:
Die Nutzung der Investitionsanlage, hier z.B. eine Produktionsanlage führt zu einem Verschleiß und folglich zu einem Wertverzehr. Damit dieser im Rahmen der Kostenvergleichsrechnung berücksichtigt wird, berechnet man die kalkulatorischen Abschreibung wie folgt:
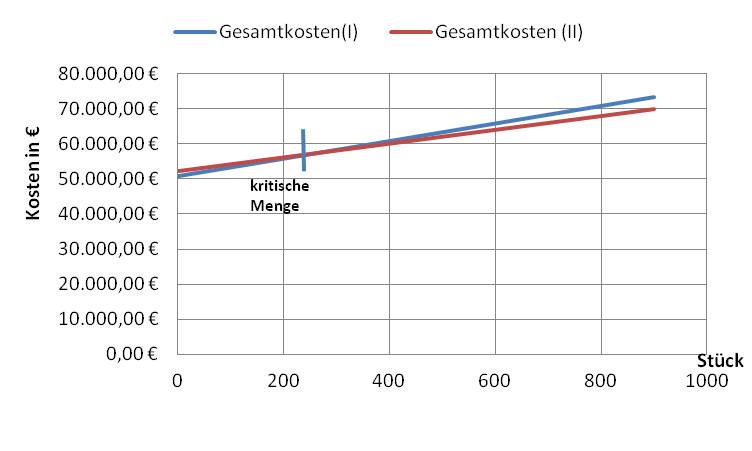
Da die Kapazität bei beiden Anlagen unterschiedlich hoch ist, muss eine Stückkostenvergleichsrechnung durchgeführt werden. Wäre die Kapazität bei beiden gleich hoch, würde ein Gesamtkostenvergleich ausreichen.
|
Produktionsanlage I |
Produktionsanlage II |
|
| Kalk. Abschreibungen vom Wiederbeschaffungswert (Berücksichtigung des Preisindex von 105 bzw. 1,05) | 260.000,00 * 1,05 / 10 = 27.300,00 € | 210.000,00 * 1,05 / 10 = 22.050,00 € |
| + kalkulatorische Zinsen
(von den Anschaffungskosten!) |
260.000,00 * 0,05 / 2 = 6.500,00 € | 210.000,00 * 0,05 / 2 = 5.250,00 € |
| + sonstige Fixkosten | 17.000,00 € | 25.000,00 € |
| = Summe Fixkosten | 50.800,00 € | 52.300,00 € |
| + variable Kosten | 20.000 * 25,10 = 502.000,00 € | 19.5000 * 19,50 = 380.250,00 € |
| = Gesamtkosten | 552.800,00 € | 432.550,00 € |
| : produzierte Menge | 20.000 | 19.500 |
| = Gesamtkosten je Stück | 27,64 € | 22,18 € |
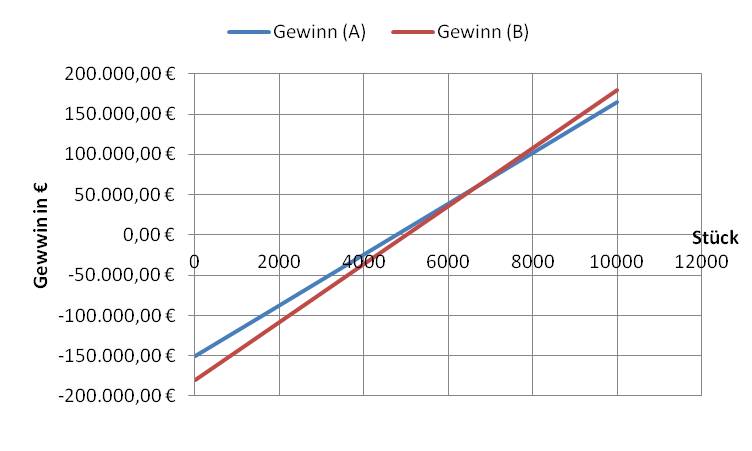
Entscheidung: Nach Durchführung der Kostenvergleichsrechnung sollte sich die FAHRRADWELT AG für Produktionsanlage II entscheiden, da hier die geringeren Gesamtkosten je Stück anfallen.Berechnung der kritischen Ausbringungsmenge:
Bei schwankenden Absatzzahlen ist die Berechnung der kritischen Ausbringungsmenge sinnvoll. Mit ihr ist eine Aussage möglich, bei welcher Ausbringungsmenge der Vorteil wechselt. Die kritische Menge ist die Menge am Markt, bei der die Gesamtkosten der beiden Investitionsalternativen gleich hoch sind.
Gesamtkosten (Investition A) = Gesamtkosten (Investition B)
kv (Investition A) * x + Kfix (Investition A) = kv (Investition B)* x + Kfix (Investition B)
Berechnung am Beispiel:
25,10 * x + 50.800,00 = 19,50 * x + 52.300,00
5,60 x = 1.500,00
x = 268 Stück (267,85714)
Bis zu einer Stückzahl von 268 Stück ist die Produktionsanlage I kostengünstiger. Dies ist auch inxd der untenstehenden Grafik beim Schnittpunkt der beiden Funktionen zu erkennen.
2) Die Gewinnvergleichsrechnung
In der Regel reicht ein Kostenvergleich in der Praxis nicht aus. Nimmt man an, dass die Investitionsalternativen unterschiedliche Erlöse erwirtschaften z.B. aufgrund eines Qualitätsunterschieds verschiedener Maschinen etc., so ist eine Kostenvergleichsrechnung nicht mehr aussagefähig genug.
Im Rahmen der Gewinnvergleichsrechnung gilt die Alternative mit dem höchsten Gewinn als vorteilhafteste. Bei unterschiedlichen Anschaffungskosten der Investitionsalternativen, wird trotzdem die Alternative mit dem höchsten Gewinn bevorzugt, da der Kapitaleinsatz nur indirekt über die kalkulatorischen Zinsen sowie über die kalkulatorische Abschreibung miteinfließt.
Die Entscheidung richtet sich nach dem Periodengewinn (= Erlöse – Kosten). Die Ermittlung der kritischen Ausbringungsmenge wird dann notwendig, wenn die Ausbringungsmenge variiert.
Kritisch ist der zeitliche Unterschied zwischen Ein- und Auszahlungen zu sehen. Im Rahmen der statischen Verfahren wird der Faktor Zeit außen vor gelassen. Zudem können Probleme auftauchen, wenn man die Erlöse nicht den Investitionsobjekten zurechnen kann. Eine Maschine führt bspw. nur einen kleinen Produktionsschritt bei der Fertigung mehrerer verschiedener Produkte durch.
Berechnung am Beispiel:
Aufgrund einer qualitativ höheren Verarbeitung kann auf Produktionsanlage I je Stück ein Erlös von 29,70 € erzielt werden. Der Erlös je Stück auf Produktionsanlage II beträgt 23,20 €.
|
Produktionsanlage I |
Produktionsanlage II |
|
| Umsatz | 594.000,00 € (29,70 * 20.000) | 452.400,00 € (23,20 * 19.500) |
| – Gesamtkosten (vgl. 1) | 552.800,00 € | 432.550,00 € |
| = Gewinn | 41.200,00 € | 19.850,00 € |
Entscheidung: Nach Durchführung der Gewinnvergleichsrechnung sollte sich die FAHRRADWELT AG für Produktionsanlage I entscheiden, da hier der höhere Gewinn erzielbar ist.
Die Gewinnfunktionen lassen sich grafisch darstellen. Hier ist auch gut zu erkennen, wann die jeweiligen Produktionsanlagen Gewinn erzielen.
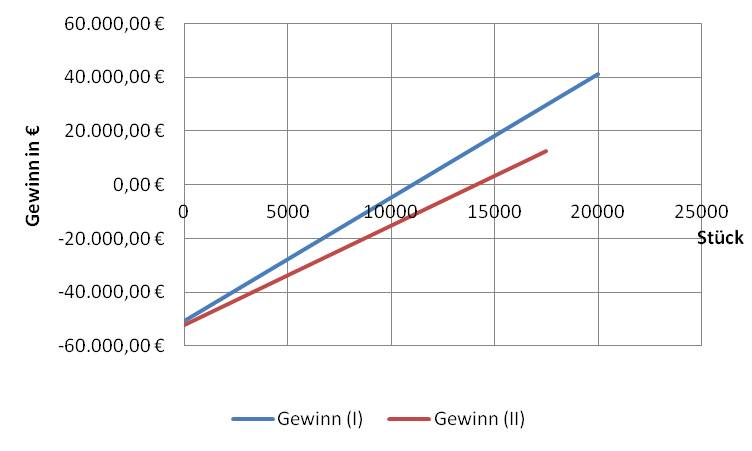
Berechnung der kritischen Ausbringungsmenge:
Ist es nicht möglich die Absatzzahlen sicher vorherzusagen, so ist die Ermittlung der kritischen Ausbringungsmenge nötig.
Gewinn (Investition A) = Gewinn (Investition B)
e (Inv. A) * x – (kv (Inv. A) * x+Kfix (Inv. A)) = e (Inv. B)* x -(kv (Inv. B) * x +Kfix (Inv. B))
Berechnung am Beispiel:
29,70 * x – (25,10 * x + 50.800,00) = 23,20 * x – (19,50 * x + 52.300,00)
29,70 * x – 25,10 * x – 50.800,00 = 23,20 * x – 19,50 * x – 52.300,00
4,60 * x – 50.800,00 = 3,70 * x – 52.300,00
0,90 x = -1.500,00
x= -1.666,666 (rechnerische Lösung)
Es ergibt sich eine negative kritische Ausbringungsmenge. Allerdings können Stückzahlen nur positiv sein, demzufolge liegt in diesem Szenario keine Gewinngleichheit (kein Schnittpunkt im positiven Bereich, siehe Grafik oben) vor.
Berechnung des Break-even-Points einer Anlage
Ist die Frage, ob ein Unternehmen überhaupt investieren sollte oder ob Risiken bei Beschäftigungsgradänderungen vorkommen, ist es hilfreich, den Break-even-Point einer Anlage zu berechnen.
Berechnung am Beispiel:
|
Produktionsanlage I |
Produktionsanlage II |
|
| db | 4,60 € (
29,70 -25,10) |
3,70 € (23,20 -19,50) |
| Kfix | 50.800,00 € | 52.300,00 € |
| x BEP | 50.800,00 / 4,60 = 11.044 St.(11.043,4782) | 52.300,00 / 3,70 = 14.136 St.(14.135,13514) |
(3) Die Rentabilitätsrechnung
Mit dieser Methode wird dem erzielten Gewinn das eingesetzte Kapital gegenübergestellt. Es wird demnach überprüft, ob und wie sich eine Investition rentiert. Zu dem Gewinn werden auch die kalkulatorischen Zinsen gerechnet. Dies hat den Hintergrund, da diese bei der Kalkulation der Verkaufserlöse berücksichtigt und somit vom Kunden bezahlt werden. Das eingesetzte Kapital entspricht dem durchschnittlich gebundenen Kapital, somit also den halben Anschaffungskosten. Die Berechnung erfolgt nach folgender Formel:
Berechnung am Beispiel:
Hinweis: Die kalk. Zinsen werden lediglich aus kostenrechnerischen Gründen erfasst und nicht tatsächlich bezahlt. Folglich wäre der Gewinn um diesen Betrag höher, wenn diese nicht eingerechnet werden würden. Aus diesem Grund werden sie wieder addiert. Dies ist aber nur dann notwendig, wenn die Investition zu 100% aus Eigenmitteln finanziert wurde.
|
Produktionsanlage I |
Produktionsanlage II |
|
| Gewinn nach Zinsen (vgl. 2) | 41.200,00 € | 19.850,00 € |
| + kalkulatorische Zinsen (vgl. 1) | 6.500,00 € | 5.250,00 € |
| = Gewinn vor Zinsen | 47.700,00 € | 25.100,00 € |
| : Ø gebundenes Kapital | 260.000,00 / 2 =
130.000,00 € |
210.000,00 /2 = 105.000,00 € |
| = Rentabilität | 36,69 % (0,3669) | 23,90 % (0,2390) |
Entscheidung: Aus Rentabilitätserwägungen wird Produktionsanlage I gewählt.
(4) Amortisationsrechnung
Die vorangegangenen Methoden berücksichtigen nur eine Abrechnungsperiode z.B. ein Geschäftsjahr. Es wird demzufolge unterstellt, dass sowohl Kosten, Erlöse als auch Gewinne in den folgenden Jahren konstant bleiben, was in der Praxis i.d.R. nicht so (z.B. Absatzschwankungen, Konkurrenzzuwachs) ist.
Im Fokus dieser Methode steht die sog. Amortisationsdauer, also die Dauer, die notwendig ist, die ursprünglichen Anschaffungskosten durch die Zahlungsmittelrückflüsse der Investition zu refinanzieren. Das Objekt mit der kürzeren Amortisationsdauer ist zu bevorzugen. Die Berechnung der Amortisationsdauer zu erfolgt nach folgender Formel:
|
Berechnung am Beispiel:
|
||||||||||||||||||||||||
| Die oben vorgestellten Investitionsrechenverfahren berechnen ausschließlich quantifizierbare Einflussgrößen wie z.B. Rentabilität, Amortisationsdauer. Daneben spielen für ein Unternehmen allerdings auch qualitative Aspekte eine bedeutende Rolle (nicht messbare Einflussgrößen). Darunter fallen bspw. ökologische Einflussgrößen, Image des Lieferanten, Sicherheit für Mitarbeiter oder Serviceleistungen des Lieferanten. |
Statische Investitionsrechenverfahren und Kreditfinanzierung: Aufgaben
Testen Sie Ihr Wissen an folgenden Beispielen:
Aufgaben:
|
Anlage A |
Anlage B |
|
| Anschaffungskosten |
580.000,00 € |
680.000,00 € |
| Nutzungsdauer |
8 Jahre |
8 Jahre |
| Preisindex
(bezogen auf Nutzungsdauer) |
109 |
109 |
| Kapazität |
8.000 Stück |
10.000 Stück |
| Fixe Kosten |
53.575,00 € |
66.950,00 € |
| Fertigungslöhne |
20,00 €/Stück |
17,50 €/Stück |
| Fertigungsmaterial |
10,50 €/Stück |
8,50 €/Stück |
Für das nächste Teammeeting soll ein Entscheidungsvorschlag für eine Investitionsalternative auf Basis des erzielbaren Gewinns unterbreitet werden. Die zukünftige Marktentwicklung mit steigendem Absatzpotential soll dabei zwingend beachtet werden.
1.1 Geben Sie eine begründete Empfehlung ab, welche Anlage beschafft werden soll.
1.2 Stellen Sie zur Visualisierung des Entscheidungsvorschlags die Situation in einer maßstabsgerechten Zeichnung grafisch dar [Maßstab: 1 cm = 1.000 Stück; 1 cm = 50.000,00 €].
1.3 Beim Teammeeting wirft ein Kollege ein, dass eine Entscheidung auf Basis des erzielbaren Gewinns problematisch sei. Erläutern Sie, ob dieser Einwand gerechtfertigt ist.
1.4 Die Spielland AG erwirbt die Anlage B. Im letzten Teammeeting wurde beschlossen, dass der Kauf der Anlage zu 75 % über ein langfristiges Darlehen (Laufzeit 10 Jahre) mit einem Zinssatz von 3,5 % p.a. und einer jährlichen Annuität von 61.323,10 € finanziert wird. Das Darlehen wird zu Beginn des neuen Geschäftsjahres aufgenommen. Erstellen Sie einen Tilgungsplan für die ersten drei Jahre und erklären Sie, wie sich das Annuitätendarlehen über die gesamte Laufzeit hinweg auf die Liquidität und den Jahresüberschuss der Spielland AG auswirkt.
1.5 Erläutern Sie zwei mögliche Beweggründe, die die Unternehmensleitung veranlasst haben könnten, nicht die gesamte Investitionssumme über einen Bankkredit zu finanzieren.
Quelle: https://www.lehrplanplus.bayern.de/sixcms/media.php/72/Übungsaufgabe_Investition%20und%20Finanzieurng.pdf, aufgerufen am 08.07.2019