Der Kondensator – Aufgaben II
Bewegung geladener Teilchen im E-Feld: Aufgaben
Bemerkung: Im neuen Lehrplan soll nicht mit geladenen mikroskopischen Teilchen, also beispielsweise Protonen oder Elektronen, gerechnet werden. Wenn man den Einfluss der Gravitation vernachlässigt, ergeben sich allerdings dieselben Rechnungen. Deshalb wird in der 1. Aufgabe mit negativen Teilchen (Elektronen) ohne Schwerkraft gerechnet. Daraufhin folgt eine 2. Aufgabe mit makroskopischem Teilchen und mit Einfluss der Schwerkraft.
Aufgabe 1
1. Die Beschleunigungsspannung \(U_{Beschl}\) eines Oszilloskop beträgt 1,20 kV.
1.1 Berechnen Sie die Geschwindigkeit der Teilchen mit der Ladung \(q=-1,6\cdot 10^{-19}\;C\) und der Masse \(m=9,109 \cdot 10^{-31}\;kg\) (Elektronen) nach der Beschleunigungseinheit.
1.2 Wie groß ist die Ablenkung und die Geschwindigkeit der Elektronen nach dem Durchlaufen des Ablenkkondensators mit der Länge 3,5 cm, dem Plattenabstand 1,00 cm und einer Ablenkspannung von 40 V?
1.3 Berechnen Sie die Gesamtablenkung auf dem vom Ablenkkondensatorende 30 cm entfernten Schirm.
Aufgabe 2
2. Eine sehr kleine Aluminium-Kugel wird an die Kante der linken Platte eines aufrecht stehenden Plattenkondensators gelegt, so dass sie sich auflädt und dann nach unten in y-Richtung mit \(g=9,81\frac{m}{s^2}\) zwischen die Platten fällt.
Wird keine Spannung angelegt, so fällt die Alu-Kugel vertikal nach unten und landet beim Ort \(x=0\) (Definition).
Der Einfachheit halber setzten wir das Potential der rechten Platte auf 0 Volt fest, Reibungseffekte sowie Luftauftrieb der kleinen Kugel werden vernachlässigt.
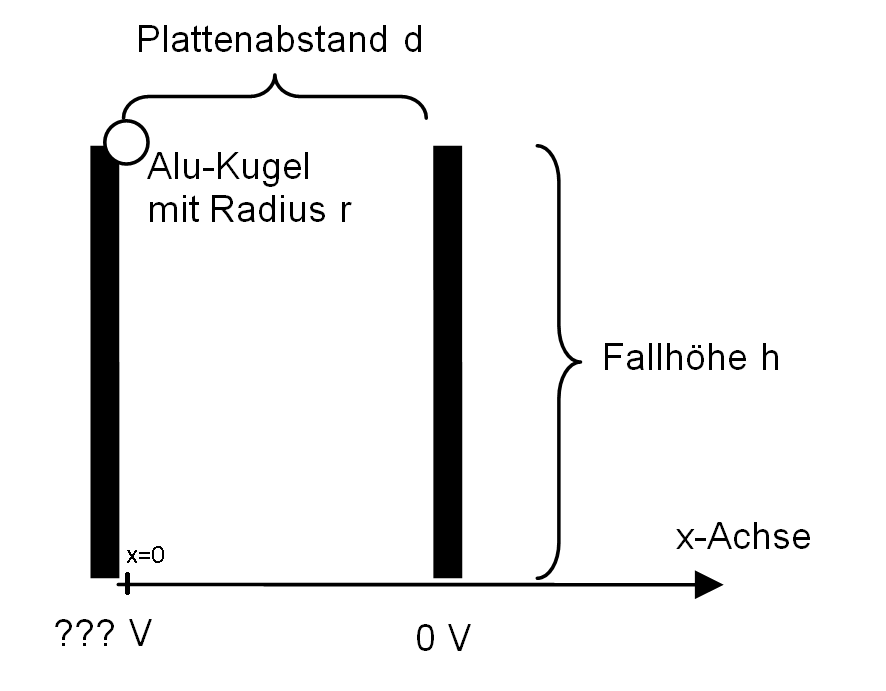
2.1 Zeichnen Sie für eingeschaltete Spannung eine plausible Bahnkurve in das Bild ein.
Berechnen Sie für die Kapazität \(C_{Alu-Kugel}=0,11\;pF\) und dem Potential +150 Volt an der linken Kondensatorplatte die Ladung auf der Alu-Kugel. Geben Sie durch allgemeine Rechnung an, welche Werte man noch wissen müsste, um die Beschleunigung in x-Richtung \(a_x\) auszurechnen.
2.2 Der Auftreffpunkt der Alu-Kugel hängt nun allein von der eingestellten Spannung ab, da diese ja gleichzeitig für das Laden der Kugel und für deren Ablenkung verantwortlich ist. Ermitteln Sie allgemein den x-Wert des Auftreffpunktes in Abhängigkeit der Spannung \(U\), also die Funktion \(x(U)\).
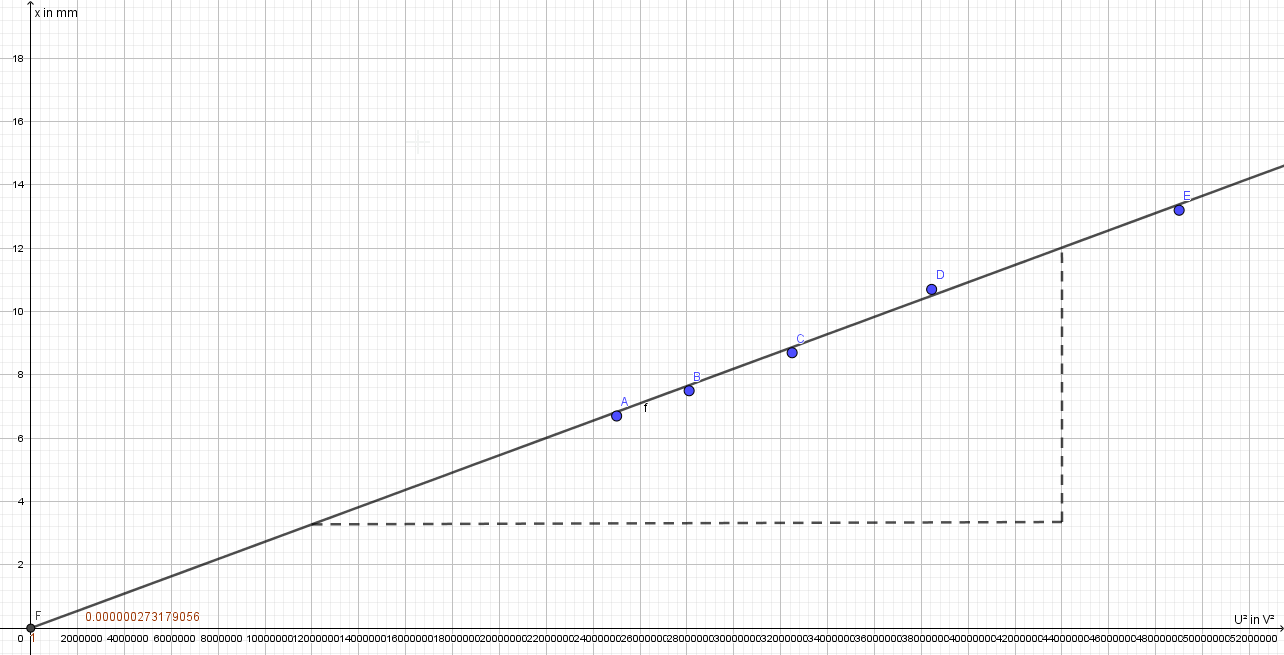
2.3 In einer Versuchsreihe wird die Spannung variiert und stets dieselbe Kugel oben an die Kante gelegt:

Tragen Sie für diese Werte das \(U^2-x-\)Diagramm auf und ermitteln Sie aus Ihrer Zeichnung die Masse der Alu-Kugel, wenn der Plattenabstand \(d=2,00\;cm\), die Fallhöhe \(h=10,0\;cm\) und die Kapazität \(C_{Alu-Kugel}=0,11\;pF\) ist.