Gini-Koeffizient
Nettoäquivalenzeinkommen (bedarfsgewichtetes Haushaltseinkommen)
Mithilfe von Äquivalenzeinkommen, auch Haushaltsäquivalenzeinkommen genannt, kann die Einkommenssituation von Haushalten unterschiedlicher Größe und Zusammensetzung vergleichbar gemacht werden. Dazu werden die Einkommen aller im Haushalt lebenden Personen addiert und mithilfe einer Bedarfsskala passend für die Struktur des Haushalts umgerechnet. Das so errechnete Äquivalenzeinkommen wird jedem Haushaltsmitglied zugewiesen, unter der Annahme, dass alle Haushaltsmitglieder in gleicher Weise vom gemeinsamen Einkommen profitieren. Dieses personenbezogene Äquivalenzeinkommen wird zum Beispiel genutzt, um die Einkommensungleichheit und das Armutsrisiko in Deutschland zu berechnen.
(Quelle: http://www.diw.de/de/diw_01.c.411605.de/presse/diw_glossar/aeguivalenzeinkommen.html)
Gini-Koeffizient
Der Gini-Koeffizient ist ein Maß zur Quantifizierung der relativen Konzentration einer Einkommensverteilung. Im Falle der maximalen Gleichverteilung der Einkommen (d. h. jede Person bezieht exakt das Durchschnittseinkommen der betrachteten Grundgesamtheit) nimmt der Gini-Koeffizient den Wert Null an, während er im anderen Extremfall einer maximal ungleichen Einkommensverteilung (d. h. eine einzige Person bezieht das komplette Einkommen der betrachteten Grundgesamtheit für sich alleine) den Wert Eins annimmt. Der Gini-Koeffizient lässt sich mithilfe der Lorenzkurve veranschaulichen und bestimmen. Der Gini-Koeffizient entspricht dabei der Fläche zwischen der Winkelhalbierenden (Gerade der perfekten Gleichverteilung) und der entsprechend ermittelten Lorenzkurve in Relation zur Gesamtfläche unterhalb der Winkelhalbierenden (Dreiecksfläche zwischen der Winkelhalbierenden und der Geraden der perfekten Ungleichverteilung).
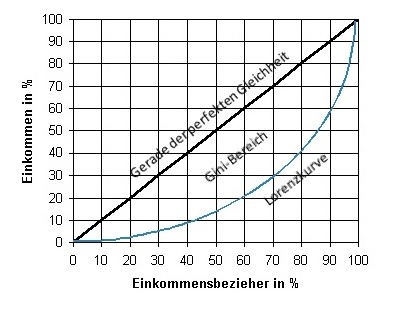
Zur Berechnung des Gini-Koeffizienten ist der Abstand zwischen der Lorenzkurve und der Winkelhalbierenden interessant, also um wie viel die beobachtete Einkommensverteilung von der Gleichverteilung abweicht. Hierzu wird der Prozentsatz des Anteils der Fläche zwischen der Winkelhalbierenden und der Lorenzkurve an der Gesamtfläche berechnet. Das Ergebnis dieser Berechnung ist der Gini-Koeffizient (G). Es gilt also:
Nimmt der Gini-Koeffizient den Wert 0 an, bedeutet das, dass es totale Gleichheit in der Einkommensverteilung gibt (die Lorenzkurve entspricht in diesem Fall der Winkelhalbierenden, die Fläche zwischen den Linien ist somit Null); der Wert 1 (Gini-Koeffizient) bringt zum Ausdruck, dass nur einem Individuum das gesamte Einkommen der Volkswirtschaft zukommt und dass das Einkommen der anderen somit Null ist (die Lorenzkurve entspricht in diesem Fall der „Linie der totalen Ungleichheit“, die Fläche zwischen der Winkelhalbierenden und der Lorenzkurve beträgt 1). Das heißt, je näher der Wert an 0 ist, desto gleicher ist die Verteilung des Einkommens. Im Allgemeinen werden Länder mit einem Gini-Koeffizienten zwischen 0,50 und 0,70 als sehr einkommensungleich, und die mit einem Gini-Koeffizienten zwischen 0,20 und 0,35 als relativ einkommensgleich bezeichnet.
Berechnungsbeispiel
Folgende Tabelle zeigt die Verteilung der Haushaltsnettoeinkommen in Deutschland 2009:
| Dezile | 1. Dezil | 2. Dezil | 3. Dezil | 4. Dezil | 5. Dezil | 6. Dezil | 7. Dezil | 8. Dezil | 9. Dezil | 10. Dezil |
| Prozent | 3,6 | 5,2 | 6,3 | 7,3 | 8,2 | 9,3 | 10,3 | 11,9 | 14,2 | 23,7 |
Somit ist n = 10, da die Gesamtheit in 10 gleich große Teile eingeteilt wird. Ai sind die kumulierten Anteile:
| Dezile | 1. Dezil | 2. Dezil | 3. Dezil | 4. Dezil | 5. Dezil | 6. Dezil | 7. Dezil | 8. Dezil | 9. Dezil | 10. Dezil |
| Prozent | 3,6 | 8,8 | 15,1 | 22,4 | 30,6 | 39,9 | 50,2 | 62,1 | 76,3 | 100 |
Die Summe aller kumulierten Anteile Ai beträgt 409 %. Somit errechnet sich der Gini-Koeffizient mit:
G = 1 – 1/10 * (2 * 4,09 – 1) = 0,282
Gini-Koeffizient im Ländervergleich
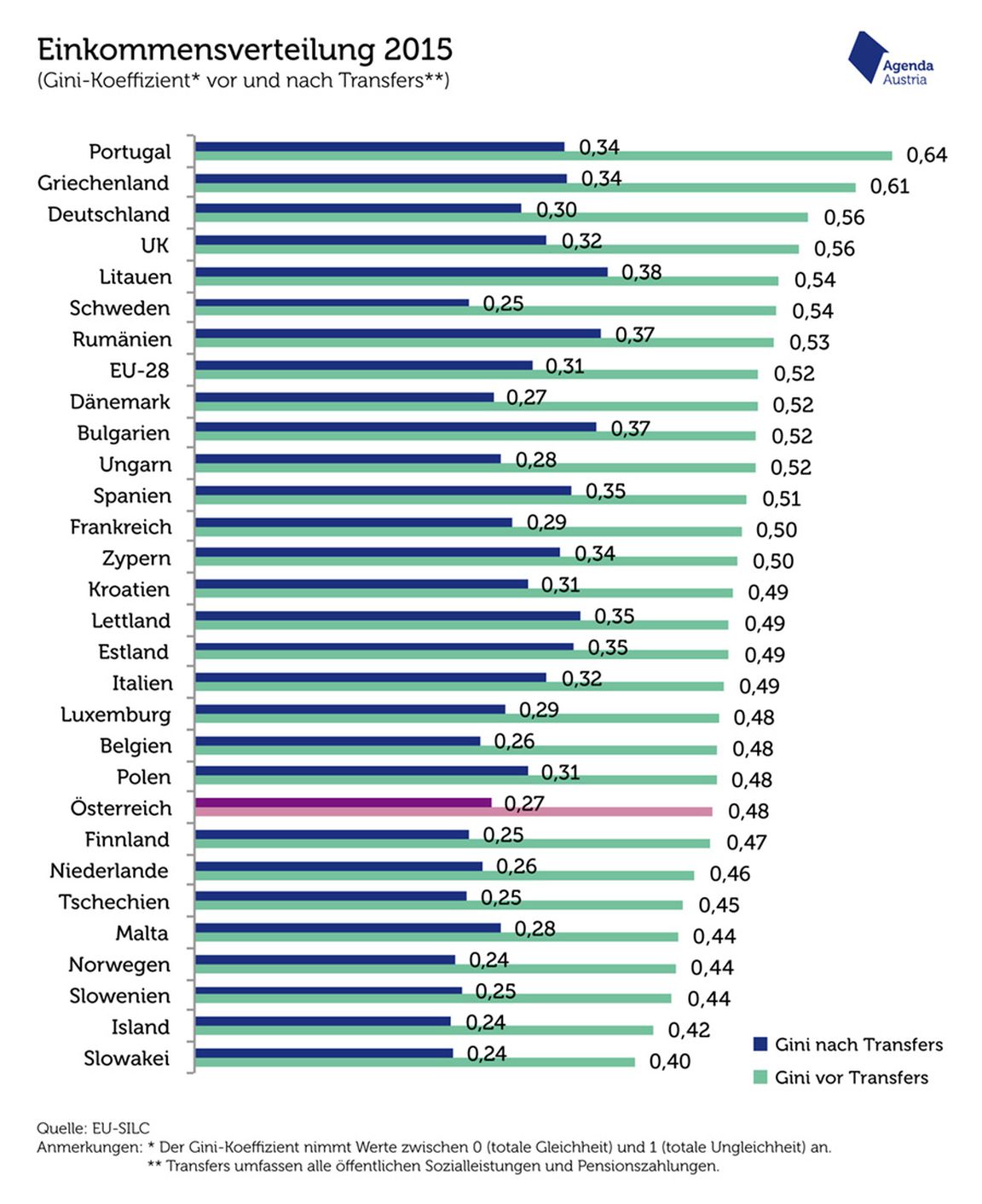
Aus der obigen Übersicht geht hervor, dass Deutschland im Vergleich der EU-Länder die drittgrößte Ungleichheit bei der Primärverteilung aufweist. Durch intensive Umverteilungsmaßnahmen erreicht Deutschland einen Platz im Mittelfeld, wenn man den Gini-Koeffizienten nach Transfers betrachtet.
Gini-Koeffizient: Aufgaben
Testen Sie Ihr Wissen an folgenden Beispielen:
(Vergleiche Abiturprüfung IBV 2016 Aufgabe II 3)
Aufgaben:
1 Nachfolgende Grafik zeigt die Verteilung des verfügbaren bedarfsgewichteten Haushaltseinkommens (Nettoäquivalenzeinkommens) nach Fünfteln (Quintilen) für die Jahre 1991 und 2010 für Deutschland:
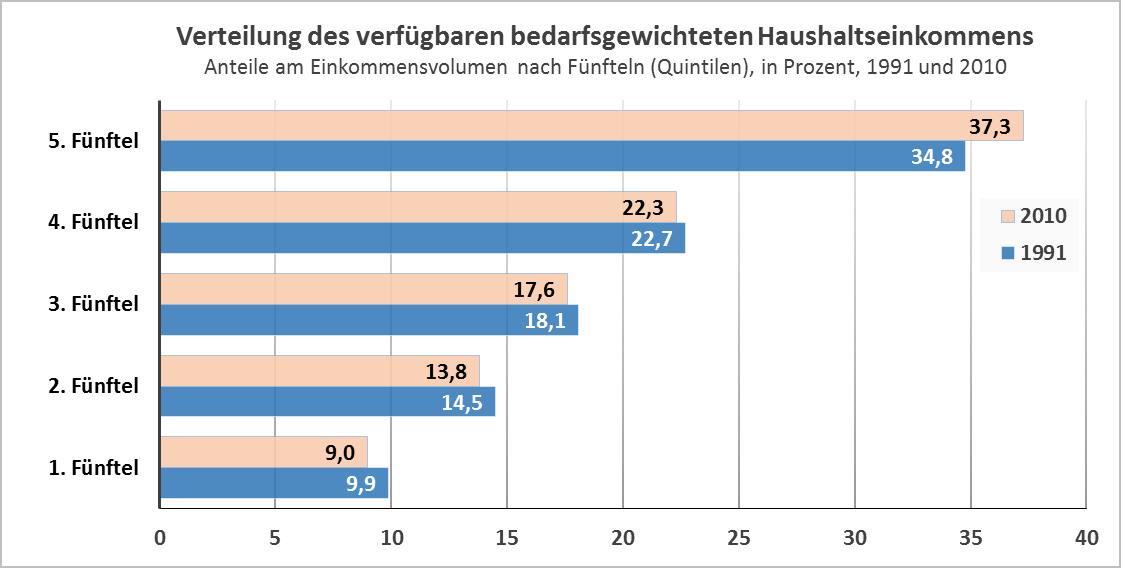
(Quelle: SOEPv28, Personen in Privathaushalten, Lizenz: Creative Commons by-nc.nd/3.0/de, Bundeszentrale für Politische Bildung, 2013, www.bpb.de, für Prüfungszwecke angepasst)
1.1 Beschreiben Sie die Entwicklung der Einkommensverteilung zwischen den Jahren 1991 und 2010.
1.2 Zur Messung der Ungleichheit der Einkommensverteilung wird sehr häufig der Gini-Koeffizient verwendet. Für das Jahr 1991 betrug dieser 0,2320.
Berechnen Sie den normierten Gini-Koeffizienten für das Jahr 2010 (auf vier Kommastellen gerundet).
Vergleichen Sie diesen mit dem des Jahres 1991 und interpretieren Sie das Ergebnis.
