Gewinnschwellenmenge bei Preis- und Kostenänderungen
Situation
Im vorherigen Einführungsbeispiel stellten wir fest, dass bei einem Verkaufspreis von 80,00 € netto die Gewinnschwelle bei 14.424 Stück erreicht wird. Wie würde sich die Nutzenschwelle nun ändern, falls wir aufgrund einer neuen Konkurrenzsituation den Preis auf 75,00 € senken müssten?
Rechnerische Lösung
| Formel für die Gewinnschwellenmenge: | m = Kf : (p – kv) |
| ↓ | ↓ |
| Einsetzen der Werte: | m = 388.000,00 : (75,00 – 53,10) = 17.716,89 also 17.717 Stück |
Ergebnis
In unserem Beispiel bewirkt eine Senkung des Preises von 80,00 € auf 75,00 € eine Erhöhung der Nutzenschwelle von 14.424 Stück auf 17.717 Stück. Bei einer Senkung des Verkaufspreises steigt also die Gewinnschwellenmenge, denn bei niedrigerem Preis müssen wir eine größere Menge absetzen um die variablen und fixen Kosten zu decken. Umgekehrt gilt: Bei einer Erhöhung des Verkaufspreises sinkt die Gewinnschwellenmenge.
Situation
Ausgehend von der Anfangssituation nehmen wir nun an, einer unserer Zulieferer erhöht seinen Preis für das Leder des Sportschuhs, so dass die variablen Kosten von 53,10 € auf 60,00 € ansteigen. Wie verändert sich nun die Gewinnschwellenmenge?
Rechnerische Lösung
| Formel für die Gewinnschwellenmenge: | m = Kf : (p – kv) |
| ↓ | ↓ |
| Einsetzen der Werte: | m = 388.000,00 : (80,00 – 60,00) = 19.400 Stück |
Ergebnis
In unserem Beispiel verursacht eine Erhöhung der variablen Kosten von 53,10 € auf 60,00 € eine Erhöhung der Nutzenschwelle von 19.400 Stück. Bei einer Erhöhung der Kosten steigt also die Gewinnschwellenmenge. Wir müssen mehr Produkte verkaufen um die gestiegenen Kosten zu decken. Umgekehrt gilt: Bei einer Senkung der Kosten sinkt die Gewinnschwellenmenge.
Situation
Damit auch andere Kunden auf unseren Laufschuh aufmerksam werden, planen wir eine Werbekampagne. Die Aktion wird monatlich 13.000,00 € kosten. Wie viele Stück müssen zusätzlich abgesetzt werden, damit diese Werbekosten gedeckt sind?
Rechnerische Lösung
| zusätzlich abzusetzende Menge = zusätzliche Fixkosten / Stückdeckungsbeitrag |
Δ m = Δ Kf / db |
| ↓ | ↓ |
| Einsetzen der Werte: | m = 13.000,00 : (80,00 – 60,00) = 650 Stück |
Ergebnis
Es müssen 650 Stück zusätzlich verkauft werden, um die Werbekosten zu erwirtschaften.
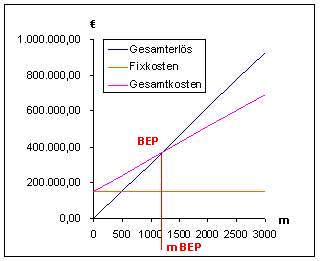
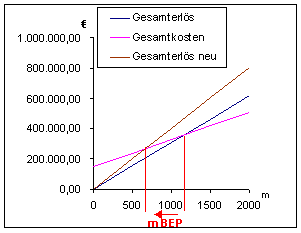
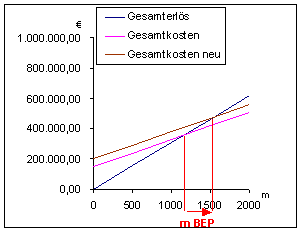
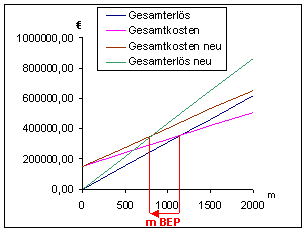
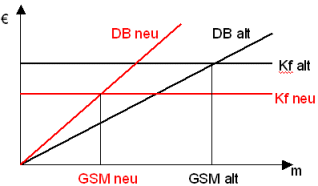
Grafische Lösung (Gesamtkostenbetrachtung)
Preis
Variable Kosten
Fixe Kosten
Ergebnis
Eine Senkung des Verkaufspreises bedeutet eine Rechtsdrehung der Erlöskurve und umgekehrt.
Eine Senkung der variablen Kosten bedeutet eine Rechtsdrehung der Kostenkurve und umgekehrt.
Eine Erhöhung der fixen Kosten bedeutet eine Parallelverschiebung der Kostenkurve nach oben und umgekehrt.
Zusammenfassung
Wie verändert sich der BEP (GSM), wenn sich einzelne Parameter ändern? Verschieben Sie die nachfolgenden Regler in der Grafik, damit Sie die Auswirkungen Grafisch nachvollziehen können.
Gewinnschwellenmenge bei Preis- und Kostenänderungen: Aufgaben 1
Testen Sie Ihr Wissen an folgenden Beispielen:
Aufgaben:
1 Ein Unternehmen verkauft Inliner. Für einen bestimmten Typ fallen 180,00 € variable Kosten an und der Nettoverkaufspreis beträgt 310,00 €. Die Fixkosten der vergangenen Periode betrugen 150.000,00 €.
1.1 Bestimmen Sie die Gewinnschwellenmenge rechnerisch und grafisch.
1.2 Ermitteln Sie, ausgehend von der Ausgangssituation, die Veränderung der Gewinnschwellenmenge rechnerisch und grafisch wenn sich
-
- der Verkaufspreis um 30% erhöht.
- die Fixkosten um 50.000,00 € erhöhen.
- sich die variablen Kosten und der Verkaufspreis um je 40% erhöhen.
2 Folgende Kostenfunktion ist gegeben: Kg (m) = 20.000 + 10,00 · m; p = 20,00 €
Berechnen Sie
- E, G, und g bei m = 300 Stück.
- die Gewinnschwellenmenge.
- die Menge, ab der die gesamten Stückkosten kleiner als 13,00 € sind.
- die Menge, bis zu der der Stückgewinn geringer als 2,00 € ist.
- die Höhe der Gesamtkosten bei einer Ausbringungsmenge von Null und 2.000 Stück.
- den Deckungsbeitragssatz.
3 Die INDUSTRIE AG fertigt in einem Zweigwerk nur das Produkt A, das einen Stückdeckungsbeitrag von 20,00 € erwirtschaftet. Die Fixkosten pro Abrechnungsperiode betragen 50.000,00 €.
3.1 Berechnen Sie die Menge, bei dem Kostendeckung erreicht wird.
3.2 Berechnen Sie den Stückpreis für Produkt A, wenn der Deckungsbeitragssatz 66 2/3 % beträgt.
3.3 In der vergangenen Periode erzielte man einen Umsatz von 120.000,00 €. Berechnen Sie, um wie viel Euro der Umsatz sinken kann, bis die Nutzenschwelle erreicht ist.
3.4 Wegen befürchteter Absatzrückgänge in der kommenden Periode plant man eine Werbeaktion (Kosten 3.000,00 €) sowie ein Sonderangebot für eine Menge von 1.000 Stück, wobei der reguläre Preis um 5% reduziert werden soll. Berechnen Sie die Menge, die zu normalen Konditionen zusätzlich abgesetzt werden muss, um das Gesamtergebnis zu halten.
3.5 Die geplanten Aktionen unter 3.4 wurden nicht realisiert. Statt dessen konnte durch Rationalisierungsmaßnahmen der Fixkostenblock um 10 % und die variablen Stückkosten um 5 % gesenkt werden.
Berechnen Sie Art und Höhe der dadurch verursachten Veränderung der Gewinnschwellenmenge und stellen Sie den Sachverhalt in einer Skizze (nicht maßstabsgetreu) zeichnerisch dar.
Lösungen
GSM = Kf : (p – kv)
= 150.000 : (310,00 – 180,00)
= 1.153,85
→ 1.154 Stück
Neuer Verkaufspreis:
p = 310,00 + 30 % = 403,00 €
Neue GSM =
150.000,00 : (403,00 – 180,00)
= 672,65
→ 673 Stück
Neue GSM = (150.000,00 + 50.000,00) : (310,00 – 180,00) = 1.538,46
→ 1.539 Stück
Neue Verkaufspreis:
p = 310,00 + 40% = 434,00 €
Neue variable Kosten:
kv = 180,00 + 40% = 252,00 €
Neue GSM = 150.000,00 : (434,00 – 252,00) = 824,18
→ 825 Stück
E = p · m = 20 · 300 = 6.000,00 €
G = E – Kf – kv · m = 6.000 – 20.000 – 10 · 300 = – 17.000,00 €
g = G : m = – 17.000 : 300 = – 56,67 €
E = K
p · m = Kf + kv · m
20 · m = 20.000 + 10 · m
m = 20.000 : 10 = 2.000 Stück (Gewinnschwellenmenge)
k = (Kf + kv · m) : m
k · m = Kf + kv · m
m · (k – kv) = Kf
m = Kf : (k – kv) = 20.000 : (13 – 10) = 6.666,67 Stück
Ab einer Menge von 6.667 Stück sind die Stückkosten kleiner als 13,00 €.
g = db – kf
g = (p – kv) – (Kf : m)
2 = 10 – 20.000 : m
8 = 20.000 : m
m = 2.500 Stück
Unter einer Menge von 2.500 Stück ist der Stückgewinn kleiner als 2,00 €.
K (0) = 20.000,00 €
K (2.000) = 20.000 + 10 · 2.000 = 40.000,00 €
DBS = 10 · 100 : 20 = 50 %
Kf = DB
50.000 = db · m
50.000 = 20 · m
m = 2.500 Stück
DBS = db : p = 66 2/3%
20 : p = 66 2/3 : 100
p = 30,00 €
Erlöse an der GSM: E = p · m = 30 · 2.500 = 75.000,00 €
120.000,00 € – 75.000,00 € = 45.000,00 €
Der Umsatz kann um 45.000,00 € sinken, bis die Gewinnschwelle erreicht wird.
| Preisreduzierung Werbemaßnahme |
30,00 · 5 % · 1.000 Stück = 1.500,00 € 3.000,00 € |
| Zusätzliche Fixkosten m = Kf : db = = 4.500,00 : 20 = 225 Stück |
4.500,00 € |
Kf neu = 50.000 – 10 % = 45.000,00 €
kv neu = 10 – 5 % = 9,50 €
db = 20,50 €
m = Kf : db = 45.000,00 : 20,50 = 2.195,1 = 2.196 Stück
m alt – m neu = 2.500 – 2.196 = 304 Stück weniger
