Gewinnschwellenmenge

Situation

Sie haben nun festgestellt, dass der Kunde für ein Paar des Laufschuhs XT 80,00 € bezahlt und dass die variablen Kosten hierbei 53,10 € und die Fixkosten insgesamt 388.000,00 € betragen. Nun stellt sich die Frage, ab welcher Verkaufsmenge die Fixkosten gedeckt sind, also ab welcher Stückzahl die Gewinnzone beginnt.

Rechnerische Lösung

An der Gewinnschwelle sind die Erlöse gleich den Gesamtkosten	E = K
↓	↓
Die Erlöse errechnen sich durch die Multiplikation des Stückpreises und der verkauften Menge:	E = p · m
↓	↓
Die Gesamtkosten sind die Summe der variablen und der fixen Gesamtkosten, wobei die Kv das Produkt der variablen Stückkosten und der verkauften Menge sind.	K = Kv + Kf = kv · m + Kf
↓	↓
Setzt man die zwei letzten Gleichungen in die erste ein, ergibt sich:	p · m = kv · m + Kf
↓	↓
Nach Ausklammern und Umstellung ergibt sich die Formel für die Gewinnschwellenmenge:	m = Kf : (p – kv) = Kf : db
↓
Nach Einsetzen der Werte: m = 388.000,00 : (80,00 – 53,10) = 14.423,79 => 14.424 Stück

Ergebnis

Bei einer verkauften Menge von 14.424 Schuhen sind also die gesamten Fixkosten gedeckt und jedes weitere verkaufte Paar erwirtschaftet einen Gewinn.

Die Menge, bei der die Erlöse den Gesamtkosten entsprechen und der Gesamtdeckungsbeitrag null ist, nennt man Gewinnschwellenmenge (GSM) oder Nutzenschwelle.

Der Umsatz bei dieser Menge wird Gewinnschwellenumsatz (UGSM) genannt und errechnet sich aus der Multiplikation der GSM mit dem Verkaufspreis.

Grafische Lösung

Vor dem Zeichnen ist es sinnvoll, ein Wertetabelle zu erstellen. Im vorliegenden Fall könnte diese so aussehen:

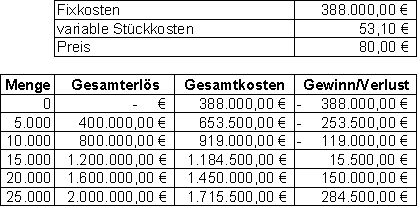
Bereits hier erkennt man, dass die Gewinnschwellenmenge zwischen 10.000 Stück und 15.000 Stück liegt, da in diesem Bereich erstmals Gewinn entsteht.

Lösung mit Gesamtkosten

Lösung mit Stückkosten

Ergebnis

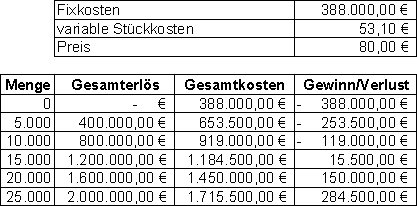
Grafisch wird der Break-Even-Punkt ermittelt, indem man den Schnittpunkt zwischen der Gesamtkostenkurve und den Erlösen bzw. dem Preis bildet. Die Gewinnschwellenmenge ergibt sich, nachdem der BEP auf die x-Achse abgetragen wurde. Links davon wird mit Verlust produziert, rechts davon mit Gewinn.

Gewinnschwellenmenge: Aufgaben

Testen Sie Ihr Wissen an folgenden Beispielen:

Aufgaben:

1 Ein Produkt verursacht monatlich fixe Gesamtkosten in Höhe 110.000,00 € und variable Kosten von 44,00 €/Stück. Der Verkaufspreis beträgt 56,50 €/Stück. Im Mai konnten 8.500 Stück produziert und verkauft werden.

1.1 Berechnen Sie den Stückdeckungsbeitrag sowie den gesamten Deckungsbeitrag für den Mai.

1.2 Ermitteln Sie rechnerisch die Gewinnschwellenmenge und stellen Sie diese in einer Skizze (nicht maßstabsgetreu) grafisch dar.

1.3 Berechnen Sie das Betriebsergebnis für das Produkt.

2 In einem Betriebsteil fallen 279.400,00 € Fixkosten an. Auf einer Produktionsanlage mit einer Kapazität von 3.800 Stück könnten die Produkte A, B oder C hergestellt werden.

Produkt A: Absatzmenge 3.000 Stück, variable Stückkosten 230,00 €, Stückpreis 450,00 €
Produkt B: Absatzmenge 2.500 Stück, variable Stückkosten 350,00 €, Stückpreis 810,00 €
Produkt C: Absatzmenge 1.300 Stück, variable Stückkosten 290,00 €, Stückpreis 620,00 €

2.1 Ermitteln Sie welches Produkt hergestellt werden sollte, damit der höchst mögliche Gewinn entsteht.

2.2 Aus absatzpolitischen Gründen entscheidet sich das Unternehmen für Produkt A. Berechnen Sie den Gewinnschwellenumsatz und den dazugehörigen Beschäftigungsgrad.

3 Auf einer Maschine der ULTRA AG wird der Camcorder des Typs Budget hergestellt. Im letzten Monat wurde die Maschine zu 80% ausgelastet (7.200 Stück). Berechnen Sie, mit welcher Kapazitätsaus-lastung die Maschine an der Nutzenschwelle arbeitet, wenn folgende Daten je Stück vorliegen:

Fertigungsmaterial 150,00 €
Fertigungslöhne 360,00 €
Spezialverpackung 14,00 €
Gemeinkosten 50,00 €, davon 40% fix
Nettoverkaufspreis 600,00 €

4 Im Zweigwerk II stellt die ULTRA AG nur das Produkt Alpha her. Eine Kostenanalyse ergibt folgende Gesamtkostenfunktion: Kg (m) = 168.000,00 + 80,00 * m
An der Kapazitätsgrenze betragen die Stückkosten 136,00 €. Die Gewinnschwellenmenge wird bei 1.050 Stück erreicht.

4.1 Berechnen Sie den Beschäftigungsgrad an der Gewinnschwelle

4.2 Um die variablen Stückkosten zu senken, wird von der Geschäftsführung der ULTRA AG über eine Rationalisierungsmaßnahme im Fertigungsbereich nachgedacht. Allerdings wäre diese Maßnahme mit einem Anstieg der fixen Kosten um 5 % verbunden.
Berechnen Sie, um welchen Betrag sich die bisherigen variablen Stückkosten verändern müssten, wenn unter sonst gleichen Bedingungen die ursprüngliche Gewinnschwelle unverändert bleiben soll.