5.4 Teilcheneigenschaften und Bildung von sauren/basischen Lösungen
5.4.1 Die Stärke von Säuren und Basen
Die Säurestärke
Protoysereaktionen sind typische chemische Gleichgewichtsreaktionen. Wendet man auf Protoysereaktionen von Säuren das Massenwirkungsgesetz an, so erhält man für das Beispiel HCl folgenden Ausdruck:
HCl + H2O ⟶ H3O+ + Cl-
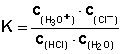
In verdünnten wässrigen Lösungen bleibt die Konzentration von Wasser jedoch annähernd gleich, so dass man sie in die Konstante K mit einbeziehen kann, ohne einen großen Fehler zu machen. (Die Konzentration von reinem Wasser beträgt übrigens 55,6 mol/l. Man errechnet diesen Wert folgendermaßen: 1 mol Wasser besitzt eine Masse von 18 g. In einem Liter Wasser, also in 1000 g sind (1000/18) mol = 55,6 mol enthalten.)
Die neue Konstante heißt Säurekonstante KS
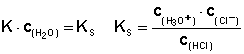
Die Größe von KS gibt Auskunft über die Lage von Protolysegleichgewichten. Ist der Wert von KS groß, so liegt das Gleichgewicht auf der Seite der Produkte. Die Säure wird als starke Säure bezeichnet. In der folgenden Tabelle (linke Hälfte) sind die sehr starken und starken Säuren rot hinterlegt, die mittelstarken rosa und die schwachen bis sehr schwachen gelb.
| Säure | KS (mol/l) | Base | KB (mol/l) | ||
| Perchlorsäure | HClO4 | 1010 | Perchlorat | ClO4– | 10–24 |
| Chlorwasserstoff | HCl | 106 | Chlorid | Cl– | 10–20 |
| Schwefelsäure | H2SO4 | 103 | Sulfat | HSO4– | 10–17 |
| Hydroniumion | H3O+ | 101,74 | Wasser | H2O | 10–15,74 |
| Salpetersäure | HNO3 | 101,32 | Nitrat | NO3– | 10–15,32 |
| Hydrogensulfat | HSO4– | 10–1,92 | Sulfat | SO42– | 10–12,08 |
| Phosphorsäure | H3PO4 | 10–1,96 | Dihydrogenphosphat | H2PO4– | 10–12,04 |
| Methansäure | HCOOH | 10–3,70 | Formiat | HCOO– | 10–10,30 |
| Ethansäure | CH3COOH | 10–4,76 | Acetat | CH3COO– | 10–9,24 |
| Kohlensäure | H2CO3 | 10–6,52 | Hydrogencarbonat | HCO3– | 10–7,48 |
| Schwefelwasserstoff | H2S | 10–6,92 | Hydrogensulfid | HS– | 10–7,08 |
| Dihydrogenphosphat | H2PO4– | 10–7,12 | Hydrogenphosphat | HPO42– | 10–6,88 |
| Ammonium | NH4+ | 10–9,25 | Ammoniak | NH3 | 10–4,75 |
| Blausäure | HCN | 10–9,40 | Cyanid | CN– | 10–4,60 |
| Hydrogencarbonat | HCO3– | 10–10,40 | Carbonat | CO32– | 10–3,60 |
| Hydrogenphosphat | HPO42– | 10–12,32 | Phosphat | PO43– | 10–1,68 |
| Wasser | H2O | 10–15,74 | Hydroxid | OH– | 101,74 |
| Hydroxid | OH– | 10–24 | Oxid | O2– | 1010 |
Die Basenstärke
Zu jeder Säure gibt es eine konjugierte Base (rechte Hälfte der Tabelle). Analog zur Definition der Säurekonstanten KS lässt sich eine Basenkonstante KB definieren (hier am Beispiel Ammoniak):
NH3 + H2O  NH4+ + OH–
NH4+ + OH–
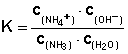
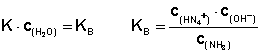
Zur Klarstellung: Bei der Protolysereaktion der Base handelt es sich nicht um die Rückreaktion der Säureprotolyse, sondern um die Reaktion der Base mit Wasser.
Betrachtet man die KB-Werte der Tabelle (rechte Hälfte der Tabelle), so zeigt sich, dass die schwächsten Basen (niedrige KB-Werte) ganz oben stehen (gelb), die stärksten Basen ganz unten (blau).
Die pKS und pKB-Werte
Es zeigt sich beim Studium der KS– und KB-Werte, dass sehr starke Säuren mit sehr schwachen Basen konjugiert sind und umgekehrt. Zwischen beiden Werten besteht ein enger Zusammenhang:
Das Produkt aus KS– und KB-Wert ergibt 10–14 (mol/l)2.
Anders ausgedrückt: Die Summe der Hochzahlen der KS– und KB-Werte ergibt -14.
Kennt man also z.B. den KS-Wert, so lässt sich über diesen Zusammenhang der KB-Wert der konjugierten Base errechnen.
Um nur noch mit Hochzahlen rechnen zu können, hat man die pKS und pKB-Werte eingeführt.
| Der pKS-Wert ist der negative dekadische Logarithmus des Zahlenwertes des KS-Wertes oder pKS = – log (KS). Der pKB-Wert ist der negative dekadische Logarithmus des Zahlenwertes des KB-Wertes oder pKB = – log (KB). |
Einfach ausgedrückt: Man erhält den pKS-Wert, indem man die Hochzahl zur Basis 10 wählt und das Vorzeichen umkehrt.
Beispiel: KS = 103 pKS = – 3.
5.4.2 Protolysegrad
Definition
Die Lage eines Protolysegleichgewichts wurde bisher durch die Gleichgewichtskonstante K bzw. bei Säuren und Basen durch die Säuren- bzw. Basenkonstante ausgedrückt. Eine zweite Möglichkeit, die Gleichgewichtslage auszudrücken, ist die Angabe des Protolysegrades a.
| Der Protolysegrad a gibt den prozentualen Anteil gelöster Teilchen an, die sich einer Protolysereaktion unterzogen haben. | |||
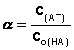 |
oder | 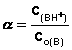 |
|
Legt man die allgemeine Reaktion HA + H2O ⇌ H3O+ + A– zugrunde, so bedeutet ein Protolysegrad von 90%, dass von 100 Molekülen HA, die in einem bestimmten Volumen Wasser gelöst sind, 90 in H3O+ + A– zerfallen sind, 10 liegen in der Lösung nach wie vor als HA vor.
Am Beispiel einer 0,1-molaren Salzsäure sei dies noch einmal verdeutlicht. Laut Tabelle (siehe unten) beträgt ihr Protolysegrad 99,9% bzw. 0,999. Damit ist Konzentration von Cl– wie auch die Konzentration von H3O+ jeweils 0,1 mol/l . 0,999 = 0,0999 mol/l.
Man muss bei der Konzentration der Säure HA also unterscheiden zwischen der Ausgangskonzentration co(HA), also der Konzentration vor der Gleichgewichtseinstellung, und der Gleichgewichtskonzentration c(HA). Der Protolysegrad a kann in Prozent oder als Bruchteil von 1 angegeben werden, also a = 90% oder 0,9.
Analog lässt sich der Protolysegrad für Basen angeben für folgende allgemeine Reaktion:
B + H2O ⇌ BH+ + OH–
Experimentell macht sich der Protolysegrad bemerkbar, wenn man die elektrische Leitfähigkeit von zwei Säuren gleicher Konzentration misst. Die Leitfähigkeit lässt sich bestimmen, indem man einen Leitfähigkeitsprüfer (zwei Elektroden) in die Lösung einbringt, eine konstante Spannung anlegt und die Stromstärke des durch die Lösung fließenden Stroms misst. Die Stromstärke hängt u.a. von der Konzentration der gelösten Ionen ab. Als Beispiele können etwa Salzsäure und Essigsäure (Ethansäure) der Konzentration 0,1 mol/l verwendet werden. Es zeigt sich, dass die elektrische Leitfähigkeit der Salzsäure um Größenordnungen über der von Essigsäure liegt. Der Grund liegt in den ganz unterschiedlichen Gleichgewichtslagen und der daraus resultierenden Unterschiede in der Ionenkonzentration.
Gleichgewicht 1: HCl + H2O ⇌ H3O+ + Cl–
Gleichgewicht 2: CH3COOH + H2O ⇌ H3O+ + CH3COO–
Während Gleichgewicht 1 extrem weit rechts liegt (großer KS-Wert, hohe Ionenkonzentration), liegt Gleichgewicht 2 weit links (kleiner KS-Wert, geringe Ionenkonzentration). Der Protolysegrad beträgt in der 0,1-molaren Salzsäure 99,9%, während er in der 0,1-molaren Essigsäure nur 1,3335% beträgt.
Die Abhängigkeit des Protolysegrades
Der Protolysegrad hängt also von der Stärke des Protolyten ab.
Dies gilt für Säuren (HCl + H2O  H3O+ + Cl–) wie für Basen (NH3 + H2O
H3O+ + Cl–) wie für Basen (NH3 + H2O  NH4+ + OH–).
NH4+ + OH–).
| Protolyt | Anfangskonz. co (mol/l) | Protolysegrad a |
| Säuren: | ||
| HCl | 0,1 | 99,9000000% |
| CH3COOH | 0,1 | 1,3335000% |
| HPO42– | 0,1 | 0,0002000% |
| Basen: | ||
| NH3 | 0,1 | 1,3335000% |
| SO42– | 0,1 | 0,0022000% |
| HSO4– | 0,1 | 0,0000010% |
Der Protolysegrad hängt aber auch von der Konzentration des Protolyten ab.
| Protolyt | Anfangskonz. co (mol/l) | Protolysegrad a |
| CH3COOH | 1,000 | 0,4217000% |
| CH3COOH | 0,100 | 1,3335000% |
| CH3COOH | 0,010 | 4,2169000% |
| CH3COOH | 0,001 | 13,3352000% |
Mit zunehmender Verdünnung der Essigsäure steigt also der Protolysegrad. Dieser Effekt ist nur bei schwachen Säuren zu beobachten. Die elektrische Leitfähigkeit nimmt beim Verdünnen von 1-molarer Essigsäure zunächst zu, bei fortgesetztem Verdünnen dann wieder ab.
Bei starken Säuren macht man diese Beobachtung nicht. Der Grund ist einfach: Wenn der Protolysegrad schon bei weit über 99% liegt, und er beim Verdünnen noch geringfügig zunähme, so würde dies keine messbare Auswirkung auf die Stromstärke haben. Die Stromstärke würde hier mit dem Verdünnen der Lösung sofort abnehmen, da der Verdünnungseffekt natürlich eine Abnahme der Gesamtionenkonzentration bedeutet.
Rechenbeispiel:
Man berechne die Konzentration der H3O+-Ionen einer 0,1-molaren Salzsäure (c(HCl) = 0,1 mol/l) und einer 0,1-molaren Essigsäure (c(CH3COOH) = 0,1 mol/l). Gibt man die Konzentration einer Säure in dieser Weise an, so ist immer die co der Säure gemeint.
Bei starken Säuren (Salzsäure, Schwefelsäure, Salpetersäure) ist von einem Protolysegrad von > 99% auszugehen. Hier kann man vereinfachend auch einen Wert von 100% zu Grunde legen. Damit nimmt man an, dass alle Säuremoleküle in der Lösung protolysiert vorliegen. Dann ist aber die co(HA) gleich der c(H3O+).
Für schwache Säuren muss die co mit dem Protolysegrad multipliziert werden, um c(H3O+) zu erhalten.
c(H3O+) = 1,3335% . 0,1 mol/l = 0,013335 . 0,1 mol/l = 0,0013335 mol/l.
