3.1.3 Massenwirkungsgesetz
Reversible Reaktionen
Chemische Reaktionen können grundsätzlich in zwei Richtungen verlaufen. Üblicherweise formuliert man sie so, dass Ausgangsstoffe (Edukte) in Endstoffe (Produkte) übergehen. Unter bestimmten Bedingungen können die Produkte aber auch wieder in die Edukte zerfallen. Chemische Reaktionen sind also reversibel, d.h. umkehrbar. Man kennzeichnet dieses Verhalten durch einen Doppelpfeil:
A + B ⇌ C + D
Zu diesem Verhalten kommt es, wenn sich eine Reaktion in einem geschlossenen Behälter abspielt, wenn also die Produkte nicht aus der Reaktionszone entweichen können.
Chemisches Gleichgewicht
Die drei abgebildeten Systeme beeinflussen den Reaktionsverlauf in unterschiedlicher Weise. Das offene System ist zu vergleichen mit einem Reagenzglas, aus dem ein gasförmiges Reaktionsprodukt entweichen kann, das mit der Umgebung aber auch Energie austauschen kann. Man kann mit dem Bunsenbrenner Energie zuführen, bei der Reaktion entstehende Energie kann an die Umgebung abgegeben werden. Verschließt man das Reagenzglas, erhält man ein geschlossenes System. Es erlaubt keinen Materieaustausch mehr mit der Umgebung, wohl aber einen Energieaustausch. Schließlich sei noch das isolierte System erwähnt. Hier ist durch geeignete thermische Isolierung auch der Energieaustausch unterbunden.
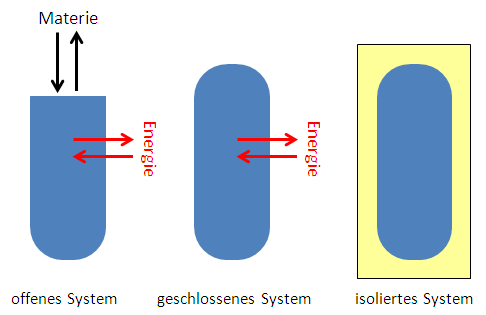
© Belinda Flemming: Energieaustausch in verschiedenen Systemen im Vergleich, CC BY-SA
Die folgenden Überlegungen zum chemischen Gleichgewicht beziehen sich auf das geschlossene System. Bringt man beliebige Mengen der Ausgangsstoffe A und B in einen geschlossenen Behälter, so reagieren die Stoffe nach C und D. Die Geschwindigkeit dieser Reaktion (Hinreaktion) ist wegen der anfänglich hohen Konzentration der Ausgangsstoffe groß. Sobald aber geringe Mengen an C und D entstanden sind, zerfallen diese auch wieder nach A und B. Es setzt also die Rückreaktion ein. Diese verläuft anfänglich mit geringer Geschwindigkeit, da die Konzentration der Endstoffe ja noch gering ist. Es lässt sich also für beide Reaktionen eine Reaktionsgeschwindigkeit angeben. Diese Geschwindigkeiten hängen jeweils von den Konzentrationen der reagierenden Stoffe ab.
Geschwindigkeit der Hinreaktion:
\(\vec { RG } = k _ { 1 } \cdot c _ { A } \cdot c _ { B }\)
Geschwindigkeit der Rückreaktion:
\(\dot { RG } = k _ { 2 } \cdot c _ { C } \cdot c _ { D }\)
Je mehr Ausgangsstoffe aber zerfallen, je geringer ihre Konzentration also wird, desto langsamer verläuft die Hinreaktion. Das Umgekehrte gilt für die Rückreaktion. Sie wird immer schneller, je mehr Endstoffe gebildet worden sind. Schließlich wird der Punkt erreicht, an dem Hin- und Rückreaktion gleich schnell verlaufen. Dieser Zustand heißt chemisches Gleichgewicht. Da genauso viele Endstoffe bebildet werden, wie gleichzeitig wieder zerfallen, ändern sich die Konzentrationen aller im System vorhandenen Stoffe nicht mehr. Nach wie vor laufen aber Hin- und Rückreaktion ab. Der Beobachter stellt aber von außen keinerlei Veränderung am System fest. Man nennt daher ein chemisches Gleichgewicht auch dynamisches Gleichgewicht.
Zusammenfassend lässt sich festhalten:
Ein chemisches Gleichgewicht stellt sich in einem geschlossenen System ein.
Im chemischen Gleichgewicht gilt:
\(\vec { RG } = \vec { R G }\)
Die Konzentrationen aller Stoffe im System sind konstant.
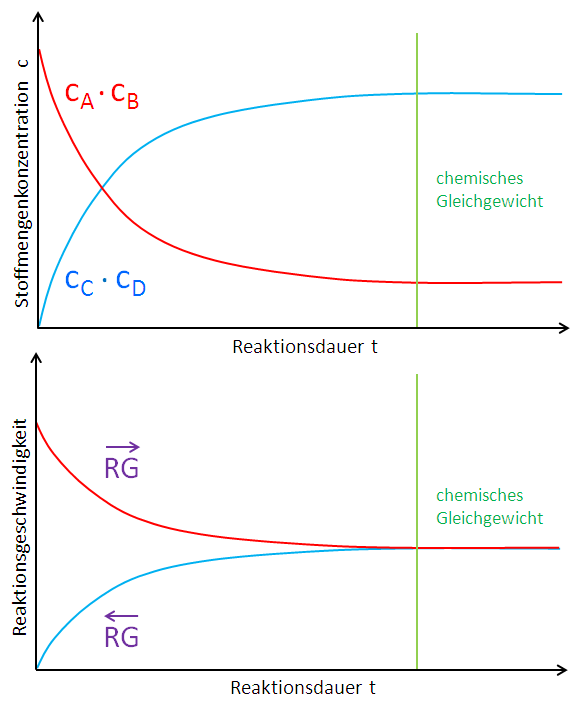
© Belinda Flemming: Einstellung des chemischen Gleichgewichtes im geschlossenen System, CC BY-SA
Die beiden Diagramme stellen diese Zusammenhänge graphisch dar. Rechts der roten Linie hat sich ein chemisches Gleichgewicht eingestellt. Die Kurven der Konzentrationen nehmen einen horizontalen Verlauf und die beiden Reaktionsgeschwindigkeiten haben sich angeglichen.
Gedankenexperiment zum chemischen Gleichgewicht
Folgendes Spiel soll zur Veranschaulichung des chemischen Gleichgewichts dienen:
Ein Gebäude besitzt zwei große Räume, die durch eine Türe verbunden sind. In Raum 1 befinden sich zu Spielbeginn 100 Personen, in Raum 2 ist niemand. Es finden mehrere Spielrunden statt, in denen Personen nach folgenden Regeln von Raum 1 in den Raum 2 gehen und umgekehrt:
Pro Spielrunde wechseln 50% der Personen des Raumes 1 in den Raum 2. Gleichzeitig wechseln 20% der zu Beginn der Runde in Raum 2 befindlichen Personen in den Raum 1.
| Spielrunde | Personen in Raum 1 | Personen in Raum 2 |
| 0 | 100 | 0 |
| 1 | 100 – 50 = 50 | 0 + 50 = 50 |
| 2 | 50 – 25 + 10 = 35 | 50 + 25 – 10 = 65 |
| 3 | 35 – 17 + 13 = 31 | 65 + 17 – 13 = 69 |
| 4 | 31 – 15 + 14 = 30 | 69 + 15 – 14 = 70 |
| 5 | 30 – 15 + 14 = 29 | 70 + 15 – 14 = 71 |
| 6 | 29 – 14 + 14 = 29 | 71 + 14 – 14 = 71 |
| 7 | 29 – 14 + 14 = 29 | 71 + 14 – 14 = 71 |
Die Parallelen zum chemischen Gleichgewicht sind offensichtlich:
Die Zahl der Personen pro Raum entspricht der Konzentration der Stoffe.
Die Zahl der Personen, die pro Zeiteinheit den Raum 1 verlassen, entspricht der Reaktionsgeschwindigkeit der Hinreaktion. Diese nimmt im Verlauf des Spiels ab. Die Zahl der Personen, die pro Zeiteinheit den Raum 2 verlassen, also die „Reaktionsgeschwindigkeit der Rückreaktion“, nimmt zu. Nach der 5. Spielrunde verändern sich die „Konzentrationen“ nicht mehr. Es hat sich ein Gleichgewicht eingestellt. Dennoch laufen weiterhin pro Runde 14 Personen von Raum 1 nach Raum 2 und umgekehrt, ohne dass sich die „Konzentrationen“ noch ändern würden. Dies symbolisiert das dynamische Gleichgewicht.
Das Massenwirkungsgesetz
Wenn im chemischen Gleichgewicht gilt:
\(\vec { RG } = \vec { R G }\)
dann gilt auch:
\(k _ { 1 } \cdot c _ { A } \cdot c _ { B } = k _ { 2 } \cdot c _ { c } \cdot c _ { D }\)
oder
\(\frac { k _ { 1 } } { k _ { 2 } } = \frac { c _ { c } \cdot c _ { D } } { c _ { A } \cdot c _ { B } } = K\)
K heißt Gleichgewichtskonstante. Der Ausdruck heißt Massenwirkungsgesetz. In seiner allgemeinsten Form, also unter Einbeziehung der in einer Reaktionsgleichung auftretenden stöchiometrischen Koeffizienten a A + b B ⇌ c C + d D, stellt sich das Massenwirkungsgesetz (MWG) so dar:
\(K = \frac { c _ { c } ^ { 0 } \cdot c _ { D } ^ { d } } { c _ { A } ^ { 3 } \cdot c _ { B } ^ { b } }\)
Anschaulicher wird dieser Ausdruck an Hand eines Beispiels. Alle an der folgenden Reaktion beteiligten Stoffe sind gasförmig. Für die Reaktion
4 NH3 + 5 O2 ⇌ 4 NO + 6 H2O(g)
lautet das MWG:
\((K = \frac { c _ { ( N 0 ) } ^ { 4 } \cdot c _ { ( H _ { 2 } 0 ) } ^ { 6 } } { c _ { ( N H _ { 0 } ) } ^ { 4 } \cdot c _ { ( 0 _ { 2 } ) } ^ { 5 } }\)
Die Einheit der Gleichgewichtskonstanten hängt von den stöchiometrischen Koeffizienten der betreffenden Reaktion ab. Im Beispiel wäre sie mol/l.
Der Begriff „Massenwirkungsgesetz“ geht auf Guldberg und Waage (1867) zurück, die die Konzentrationen als „aktive Massen“ bezeichneten.
Die Gleichgewichtskonstante
Die Gleichgewichtskonstante besitzt große praktische Bedeutung. Sie gibt Auskunft über die Lage von Gleichgewichten und damit über die Ausbeute von Reaktionsprodukten. Sie lässt sich experimentell ermitteln. Als Beispiel sei die Reaktion zwischen Wasserstoff und Ioddampf H2 + I2 ![]() 2 HI gewählt.
2 HI gewählt.
In einem Behälter (geschlossenes System!) wird eine bestimmte Menge Wasserstoff und Ioddampf auf 425°C erhitzt. Die Gase reagieren miteinander und es stellt sich eine gewisse Konzentration an Iodwasserstoffgas ein. Sobald keine Konzentrationsänderungen mehr stattfinden, misst man die Konzentrationen aller Gase im Gleichgewicht. Dabei erhält man z.B. folgende Werte:
c(H2) = 1,8313.10-3 mol/l c(I2) = 3,1291.10-3 mol/l c(HI) = 17,671.10-3 mol/l.
Setzt man diese ins MWG ein, erhält man die Gleichgewichtskonstante K:
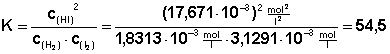
Eine Versuchsserie, bei der man von unterschiedlichsten Ausgangskonzentrationen an H2 und I2 ausging, lieferte folgende H2-, I2– und HI-Gleichgewichtskonzentrationen:
| Experiment Nr. | c(H2) (mol/l) | c(I2) (mol/l) | c(HI) (mol/l) | K |
| 1 | 1,83.10-3 | 3,13.10-3 | 17,7.10-3 | 54,5 |
| 2 | 2,24.10-3 | 2,34.10-3 | 16,9.10-3 | 53,9 |
| 3 | 2,91.10-3 | 1,71.10-3 | 16,5.10-3 | 54,7 |
| 4 | 3,56.10-3 | 1,25.10-3 | 15,6.10-3 | 54,7 |
| 5 | 4,57.10-3 | 0,74.10-3 | 13,5.10-3 | 54,6 |
| 6 | 0,48.10-3 | 0,48.10-3 | 3,53.10-3 | 54,5 |
| 7 | 0,50.10-3 | 0,50.10-3 | 3,66.10-3 | 54,3 |
| 8 | 1,14.10-3 | 1,14.10-3 | 8,41-3 | 54,6 |
| Mittelwert: | 54,3 | |||
Es zeigt sich, dass die Gleichgewichtskonstante für alle Versuche nahezu denselben Wert annimmt. K ist also unabhängig von den Ausgangskonzentrationen der in System vorhandenen Stoffe. Ändert man allerdings die Temperatur, ändert sich auch K. Die Gleichgewichtskonstante K ist also temperaturabhängig.
Abhängigkeit des chemischen Gleichgewichtes
- Abhängigkeit der Gleichgewichtslage von der Konzentration
In Stoffgemischen, die sich in geschlossenen Systemen befinden, stellen sich chemische Gleichgewichte ein. Solche Gleichgewichte lassen sich jedoch stören. Eine Möglichkeit besteht darin, dass man die Konzentration irgendeines Stoffes ändert. Dabei spielt es keine Rolle, ob ein Ausgangs- oder ein Endstoff betroffen ist, ob man die Konzentration erhöht oder erniedrigt.
Reaktionsbeispiel
Bringt man eine gelbe Eisen(III)-chloridlösung mit einer farblosen Kaliumthiocyanatlösung zusammen, entsteht das rote Eisenthiocyanat.
Ionengleichung:
Fe3+ + 3 Cl– + 3 K+ + 3 SCN– ⇌ Fe(SCN)3 + 3 K+ + 3 Cl–
oder als verkürzte Ionengleichung:
Fe3+ + 3 SCN– ⇌ Fe(SCN)3
Die Reaktion kann im offenen Reagenzglas durchgeführt werden, da ausschließlich gelöste Stoffe beteiligt sind. Das System verhält sich hinsichtlich der Gleichgewichtseinstellung nicht anders als ein geschlossenes System.
Man teilt die rote Lösung in drei Reagenzgläser auf und versetzt das erste mit weiterer FeCl3-Lösung, das zweite mit weiterer KSCN-Lösung und behält das dritte als Vergleichslösung. In den beiden ersten Reagenzgläsern beobachtet man eine weitere Farbvertiefung. Das Rot wird also noch intensiver, die Konzentration von Fe(SCN)3 in den beiden Lösungen nimmt also jeweils zu.
Formuliert man das MWG für dieses Beispiel, so erhält man den Ausdruck:
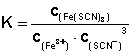
Bezogen auf die drei Versuchsansätze bedeutet dies, dass in allen drei Fällen unterschiedliche Ausgangskonzentrationen vorliegen. Entsprechend stellen sich auch unterschiedliche Gleichgewichtskonzentrationen ein. Der Wert für K ist aber in allen drei Fällen derselbe. Also müssen die Ausgangsstoffe so lange miteinander reagieren, bis sich der Wert des Nenners soweit verringert hat und sich der Wert des Zählers soweit vergrößert hat, bis der Wert für K wieder erreicht ist.
Anschaulicher mag diese Formulierung sein:
Stört man ein im chemischen Gleichgewicht befindliches System, indem man im Beispiel etwa die Konzentration von Fe3+ erhöht, so ist das System „bestrebt“, diese Störung zu minimieren, also die Konzentration von Fe3+ zu verringern. Dies ist nur durch den zeitweise vermehrten Ablauf der Hinreaktion möglich. Diese läuft also bis zur Neueinstellung eines Gleichgewichts schneller ab als die Rückreaktion. Im neu entstandenen Gleichgewicht ist dann allerdings weniger Fe3+ vorhanden. Gleichzeitig hat aber auch die Konzentration von SCN– abgenommen und die des roten Fe(SCN)3 zugenommen.
Es ist also unerheblich, ob die Konzentration von Fe3+ oder die von SCN– erhöht wird, die Folge ist immer dieselbe. Das Gleichgewicht verschiebt sich nach rechts.
Umgekehrt könnte man auch die Konzentration eines der Ausgangsstoffe erniedrigen. Das Gleichgewicht würde sich dann nach links verschieben. Genauso ließen sich die Konzentrationen der Endstoffe in einem Gleichgewicht verändern. Erhöht man die Konzentration der Endstoffe, so verschiebt sich das Gleichgewicht nach links, erniedrigt man sie, verschiebt es sich nach rechts.
Reaktionsbeispiel
Man löst das gelbe Salz Natriumdichromat (Na2CrO4) in Wasser auf und versetzt es bis zum Farbumschlag nach orange mit Salzsäure. Es stellt sich ein Gleichgewicht zwischen dem gelben Chromat-Ion und dem orangen Dichromat-Ion ein.
2 CrO42- + 2 H+ ⇌ Cr2O72- + H2O
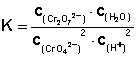
Säuert man die Lösung an, erhöht man also die Konzentration der H+– (bzw. H3O+-)Ionen, so verschiebt sich das Gleichgewicht nach rechts, wodurch die zugesetzten H+-Ionen, teilweise verbraucht werden, also die Störung verringert wird. Gleichzeitig bildet sich aber durch die vermehrte Hinreaktion auch oranges Dichromat. Das Gleichgewicht lässt sich leicht wieder nach links verschieben, indem man Lauge zugibt. Dabei werden die H+-Ionen durch die OH–-Ionen neutralisiert, also die c(H+) erniedrigt, was zu ihrer teilweisen Nachbildung führt, also zur Verschiebung des Gleichgewichts nach links. Folge ist, dass wieder ein Farbwechsel von orange nach gelb stattfindet.
- Abhängigkeit der Gleichgewichtslage von der Temperatur
Chemische Gleichgewichte lassen sich auch durch Temperaturänderungen stören. In einen geschlossenen Behälter wird braunes Stickstoffdioxid-Gas gefüllt. Das giftige NO2 lässt sich gewinnen, indem man konzentrierte Salpetersäure (HNO3) auf Kupferspäne einwirken lässt. Im geschlossenen System dimerisiert NO2 zu N2O4 (Distickstofftetraoxid), einem farblosen Gas zum Teil. Zwischen beiden Gasen stellt sich ein Gleichgewicht ein:
2 NO2 ⇌ N2O4 DHm = – 57,3 kJ/mol
Am negativen Vorzeichen ist abzulesen, dass die Hinreaktion exotherm ist, die Rückreaktion endotherm.
Im folgenden Versuch werden drei Glaskolben benötigt, die jeweils mit gleichen Gasmengen an Stickstoffdioxid gefüllt sind. Der erste wird in heißes Wasser getaucht, der zweite in kaltes Wasser, der dritte (mittlere) dient bei Raumtemperatur zum Farbvergleich.
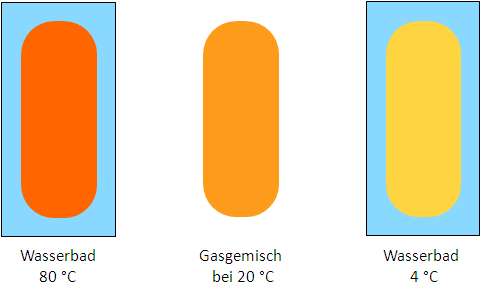
© Belinda Flemming: Temperaturabhängigkeit des chemischen Gleichgewichtes, CC BY-SA
Es zeigt sich, dass es durch die Temperaturerhöhung im ersten Kolben zu einer Verdunkelung kommt, durch die Abkühlung jedoch zu einer Farbaufhellung. Durch die Temperaturänderungen wurden bestehende Gleichgewichte gestört. Eine Temperaturerhöhung bedeutet eine Energiezufuhr. Dies ist die eigentliche Störung, die zu minimieren „versucht“ wird. Die zugeführte Energie kann aber nur durch eine Energie verbrauchende Reaktion beseitigt werden. Die Energie verbrauchende Reaktion ist aber die endotherme Reaktion, hier also die Rückreaktion. Es läuft also bis zur Neueinstellung eines Gleichgewichts die Rückreaktion schneller ab als die Hinreaktion. Dies führt im Ergebnis zur Bildung von mehr braunem Stickstoffdioxid, also zu der beobachteten Farbvertiefung bzw. Verdunkelung.
Umgekehrt wird durch das Abkühlen dem System Energie entzogen. Diese Störung wird teilweise dadurch ausgeglichen, dass die Energie liefernde Reaktion, also die exotherme Reaktion, bevorzugt abläuft. Dies führt zur vermehrten Bildung von farblosem Distickstofftetraoxid, also zur Aufhellung.
- Abhängigkeit der Gleichgewichtslage vom Druck
Diese Abhängigkeit lässt sich am selben System zeigen:
2 NO2 ⇌ N2O4
Man füllt einen Kolbenprober (Glaszylinder mit eingeschliffenem Glaskolben) mit dem unter Normaldruck rotbraunen Gas Stickstoffdioxid und übt auf das System Druck aus.
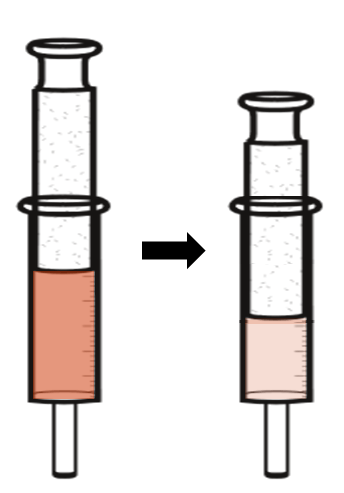
© Belinda Flemming: Druckerhöhung auf das Gas Stickstoffdioxid im Kolbenprober, CC BY-SA
Man beobachtet zunächst eine Verdunkelung des Gases, nach kurzer Zeit jedoch eine Aufhellung. Das Gas ist bei anhaltendem Druck schließlich heller als zu Beginn des Versuchs.
Es überlagern sich hier zwei Effekte: Zunächst nimmt die Dichte des Gases zu, was die Verdunkelung z.T. erklärt. Es erhöht sich aber auch die Temperatur, weshalb sich das Gleichgewicht zugunsten von NO2verschiebt, wie im vorigen Absatz erläutert. Wartet man aber kurze Zeit, bis ein Temperaturausgleich stattgefunden hat, ist das Gas heller als bei geringem Druck. Das Gleichgewicht hat sich in Richtung N2O4verschoben. Dies ist der eigentliche Effekt, der hier diskutiert werden soll.
Die Druckerhöhung stellt für das im Gleichgewicht befindliche System eine Störung dar, die es zu minimieren „versucht“. Der Druck im System kann dadurch abgebaut werden, dass die Zahl der Gasteilchen vermindert wird. Dies geschieht durch die Hinreaktion, die bis zur Neueinstellung des Gleichgewichts vermehrt abläuft. Bei der Hinreaktion vereinigen sich zwei Teilchen NO2 zu einem Teilchen N2O4. Die Zahl der Gasmoleküle nimmt also ab, was gleichzeitig den Druck mindert uns so die Störung minimiert. Dabei ist die Größe der Teilchen unerheblich. Der Druck eines Gases wird bei konstanter Temperatur und einem gegebenen Volumen allein von der Zahl der Teilchen bestimmt. Grundlage für diese Aussage ist der Satz von Avogadro, wonach gleiche Volumina unterschiedlicher Gase bei gleichen Bedingungen (Druck, Temperatur) gleich viele Teilchen enthalten.
Das Prinzip vom kleinsten Zwang
Die drei besprochenen Abhängigkeiten chemischer Gleichgewichte lassen sich im Prinzip vom kleinsten Zwang (nach Braun und Le Chatelier) zusammenfassen:
Die Rolle eines Katalysators
Ein Katalysator beeinflusst die Lage von chemischen Gleichgewichten nicht. Er beschleunigt ja Hin- und Rückreaktion gleichermaßen. Damit erleichtert bzw. ermöglicht er überhaupt erst die Einstellung chemischer Gleichgewichte. Für viele großtechnische Verfahren spielen Katalysatoren aber genau aus diesem Grunde eine wichtige Rolle.
