2.2.4 Orbitalmodell und Elektronenverteilung
Welle-Teilchen-Dualismus
Der französische Forscher Louis de Broglie hatte die Idee, dass Elektronen ähnlich wie die Photonen des Lichts sich nicht nur als Teilchen sondern auch als Welle auffassen ließen. Experimente bestätigten diese Überlegung. So kann ein Elektronenstrahl in einem Kathodenstrahlrohr ein Flügelrad antreiben. Die Elektronen verhalten sich hier also wie Teilchen. Es gibt aber auch Erscheinungen, die sich mit diesem Modell nicht erklären lassen.

By Lookang many thanks to Fu-Kwun Hwang and author of Easy Java Simulation = Francisco Esquembre – Own work, CC BY-SA 3.0, Link
Von Wasserwellen, die zwischen Hindernissen hindurchtreten müssen, weiß man, dass sie sich von dort aus kreisförmig ausbreiten. Diese Wellenkreise überlagern sich. Dabei kommt es zu der Erscheinung, dass sich Wellenberge gegenseitig verstärken bzw. Wellenberg und Wellental sich gegenseitig auslöschen. Das entstehende Muster auf der Wasseroberfläche nennt man Interferenzmuster.
Lässt man Elektronen in geeigneten Experimenten durch ein Kristallgitter treten, so tritt ebenfalls ein Interferenzmuster auf.
Links:
Modell eines NaCl-Kristalls
Rechts:
Elektronen-
interferenz-
muster des Kochsalzes
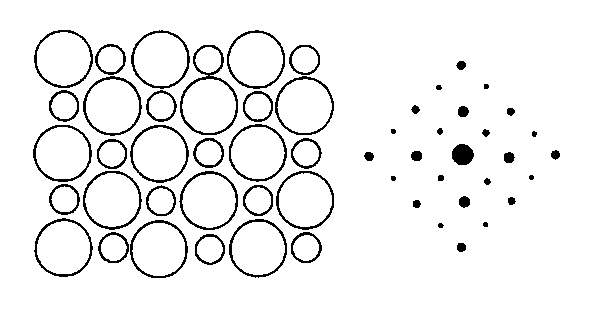
© Belinda Flemming: Modell eines Ionengitters, z.B. NaCl (links), Elektroneninterferenzmuster (rechts), CC BY-SA
Der Orbitalbegriff
Weitere Änderungen erfuhr das Atommodell durch neue Entwicklungen in der Quantenphysik. Die Quantenmechanik spricht nicht von der exakten Position eines Teilchens. Vielmehr spricht sie von der Wahrscheinlichkeit ein Teilchen an einem bestimmten Ort anzutreffen (Heisenbergs Unschärferelation). Der mathematische Ausdruck, der die Aufenthaltswahrscheinlichkeit für ein Elektron angibt, ist die Wellenfunktion Ψ.
Die Werte für die Wellenfunktion sind für manche Orte hoch, für andere niedrig. Die Wahrscheinlichkeit, ein Elektron an einem bestimmten Ort anzutreffen, ist dem Quadrat von Ψ proportional. Die graphische Darstellung der Wellenfunktion eines Elektrons heißt Atomorbital. Ein Atomorbital (kurz: Orbital) ist als Ort mit einer hohen Aufenthaltswahrscheinlichkeit für das Elektron definiert (üblicherweise 90%). Ein Wasserstoffatom besitzt also eine Reihe verschiedener Orbitale (Aufenthaltsräume für Elektronen). Wechselt das Elektron sein Orbital, so kann dies mit einer Energieaufnahme oder -abgabe verbunden sein.
Die Gleichung zur Berechnung der Atomorbitale des Wasserstoffatoms wurde von dem Österreicher Erwin Schrödinger 1926 formuliert und zu seinen Ehren nach ihm Schrödinger-Gleichung genannt. Die Lösungen dieser Differentialgleichung liefert die Formen der Orbitale.
Die Quantenzahlen
Die Hauptquantenzahl n entspricht den Energieniveaus des Bohrschen Atommodells. Sie nimmt die Werte n = 1, 2, 3 usw. an; n = 1 entspricht dabei der K-Schale, n = 2 der L-Schale usw.. Auf diesen Energieniveaus oder Schalen findet man Unterschalen bzw. Orbitale. Ihre Zahl beträgt n2. Die K-Schale besteht also nur aus einem Orbital, die L-Schale besitzt 4 Orbitale, die M-Schale 9.
Die Nebenquantenzahl l charakterisiert eine Gruppe ähnlicher Orbitale, die zu einer Schale gehören. Die Nebenquantenzahl kann die Werte 0, 1, … bis n – 1 annehmen. Für n = 1 kann l also nur 0 sein. Die K-Schale besteht also nur aus einem Orbital, wie bereits festgestellt. Für n = 2 kann l die Werte 0 und 1 annehmen, d.h. es gibt auf der L-Schale zwei Orbitalarten. Orbitale der Nebenquantenzahl l = 0 werden auch als s-Orbital bezeichnet, solche der Nebenquantenzahl l = 1 als p-Orbitale:
| Nebenquantenzahl l | 0 | 1 | 2 | 3 |
| Orbitalart | s | p | d | f |
Die magnetische Quantenzahl m charakterisiert das individuelle Orbital innerhalb einer Gruppe, z.B. innerhalb der p-Orbitale der L-Schale. Durch diese Quantenzahl wird das Verhalten des Elektrons im Magnetfeld bestimmt. Die p- bzw. d-Niveaus einer Schale sind energetisch gleich. Werden jedoch Spektraluntersuchungen im magnetischen Feld vorgenommen, so können sie in drei bzw. fünf Niveaus aufgespalten werden, die sich allerdings energetisch nur geringfügig unterscheiden (Zeemann-Effekt). Die magnetische Quantenzahl kann die Werte +l, … 0 … -l annehmen. Für l = 0 (s-Orbital) kann m nur 0 sein. Dies bedeutet, dass es auf jeder Schale nur ein s-Orbital gibt. Für l = 1 (p-Orbital) kann m die Werte -1, 0, +1 annehmen. Es existieren also drei p-Orbitale pro Schale. Für l = 2 (d-Oribtal) kann m also fünf Werte annehmen und für l = 3 (f-Orbital) sieben Werte. Dies heißt, dass d-Orbitale in Gruppen zu je fünf und f-Orbitale in Gruppen zu je sieben Orbitalen vorkommen.
Die Spinquantenzahl s: Bei genauer Untersuchung der Wasserstoffspektren stellte man fest, dass die den Linien zugrunde liegenden Frequenzen nicht exakt mit den Berechnungen Schrödingers übereinstimmten. Dies liegt am Eigendrehimpuls der Elektronen oder dem Spin. Dieser kann nur zwei Werte annehmen +1/2 und -1/2.
Im Überblick:
| n | l | Orbital | m | s | Anzahl der Kombinationen |
| 1 | 0 | 1s | 0 | (+ frac , – frac ) | 2 |
| 2 | 0 | 2s | 0 | (+ frac , – frac ) | 2 |
| 2 | 1 | 2p | +1, 0, -1 | (+ frac , – frac ) | 6 |
| 3 | 0 | 3s | 0 | (+ frac , – frac ) | 2 |
| 3 | 1 | 3p | +1, 0, -1 | (+ frac , – frac ) | 6 |
| 3 | 2 | 3d | +2, +1, 0, -1, -2 | (+ frac , – frac ) | 10 |
| 4 | 0 | 4s | 0 | (+ frac , – frac ) | 2 |
| 4 | 1 | 4p | +1, 0, -1 | (+ frac , – frac ) | 6 |
| 4 | 2 | 4d | +2, +1, 0, -1, -2 | (+ frac , – frac ) | 10 |
| 4 | 3 | 4f | +3, +2, +1, 0, -1, -2, -3 | (+ frac , – frac ) | 14 |
Die Orbitalarten
Die Orbitalformen ergeben sich als dreidimensionale Darstellungen der Wahrscheinlichkeitsverteilung für die Aufenthaltswahrscheinlichkeit von Elektronen um den Atomkern. Entsprechend der Definition besitzt also ein Orbital keine scharfe Abgrenzung (siehe Abb. 1s-Orbital). Aus Gründen der Deutlichkeit sind die p- und d-Orbitale mit einer Begrenzungslinie dargestellt. Diese schließt also den Raum ein, für den die Aufenthaltwahrscheinlichkeit für Elektronen 90% beträgt.
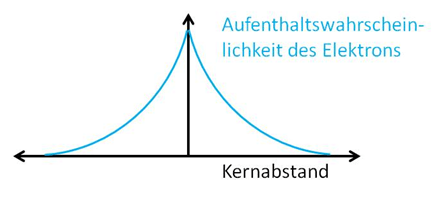
© Belinda Flemming: s-Orbital, CC BY-SA
Für das 1s-Orbital des Wasserstoffs ist die Wahrscheinlichkeit, das Elektron anzutreffen, in Kernnähe am größten. Das 1s-Orbital ist kugelförmig.
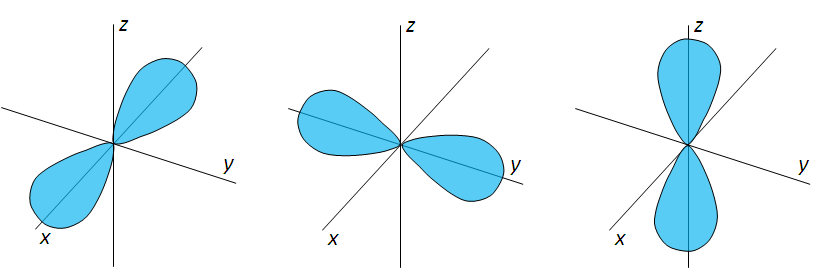
© Belinda Flemming: räumliche Lage der p-Orbital, CC BY-SA
Für p-Orbitale existieren Knotenebenen. In Kernnähe sinkt die Wahrscheinlichkeit, ein Elektron in einem solchen Orbital anzutreffen, gegen null. Dementsprechend sind p-Orbitale hantelförmig.
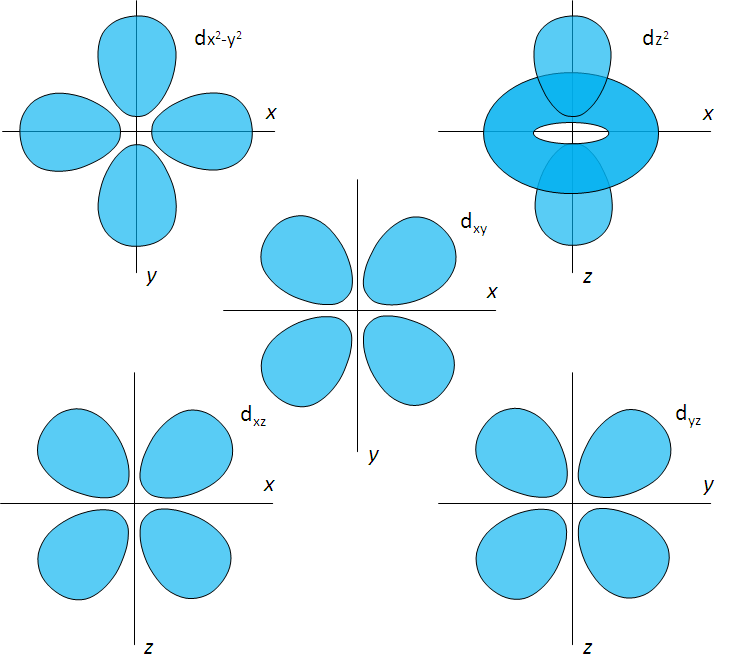
© Belinda Flemming: räumliche Lage der d-Orbital, CC BY-SA
Die Zahl der Knotenebenen nimmt mit steigender Nebenquantenzahl zu. Noch komplizierter sind f-Orbitale gebaut.
Elektronenverteilung in der Atomhülle
Die Orbitalarten und die maximale Elektronenzahl verteilen sich auf die Schalen in folgender Weise:
(Die Tabelle ist von unten nach oben zu lesen!)
| Schale | Orbitalart | Maximale Elektronenzahl 2n² |
| N (n = 4) | ein 4s-Orbital, drei 4p-Orbitale, fünf 4d-Orb., sieben 4f-Orb. | 32 |
| M (n = 3) | ein 3s-Orbital, drei 3p-Orbitale, fünf 3d-Orbitale | 18 |
| L (n = 2) | ein 2s-Orbital, drei 2p-Orbitale | 8 |
| K (n = 1) | ein 1s-Orbital | 2 |
Auch für die O-Schale und alle weiteren existieren in der Realität nur die Orbitale s bis f. Auf jedem Orbital finden 2 Elektronen Platz. Wenn also in der M-Schale ein s-Orbital, drei p-Orbitale und fünf d-Orbitale existieren, also neun Orbitale insgesamt, so können diese maximal 18 Elektronen aufnehmen. Die maximale Elektronenzahl pro Schale lässt sich auch nach der Formel 2n2 ermitteln.

By Roshan220195 – Own work, CC BY-SA 3.0, Link
Zellenschreibweise und Energieniveauschema
Auf den amerikanischen Chemiker Linus Pauling geht die Darstellungsweise der Orbitale in der Zellenschreibweise zurück. Dabei werden Orbitale als „Zellen“, die Elektronen darin als Pfeile dargestellt.
Im folgenden Energieniveauschema wird eine leere Atomhülle mit Elektronen aufgefüllt. Dabei finden die drei o.g. Regeln Anwendung. Zweckmäßigerweise verfolgt man die Besetzung der Orbitale im Periodensystem mit. Weiterhin wurden die Quantenzahlen für ein Elektron (pink) dargestellt und ermittelt.
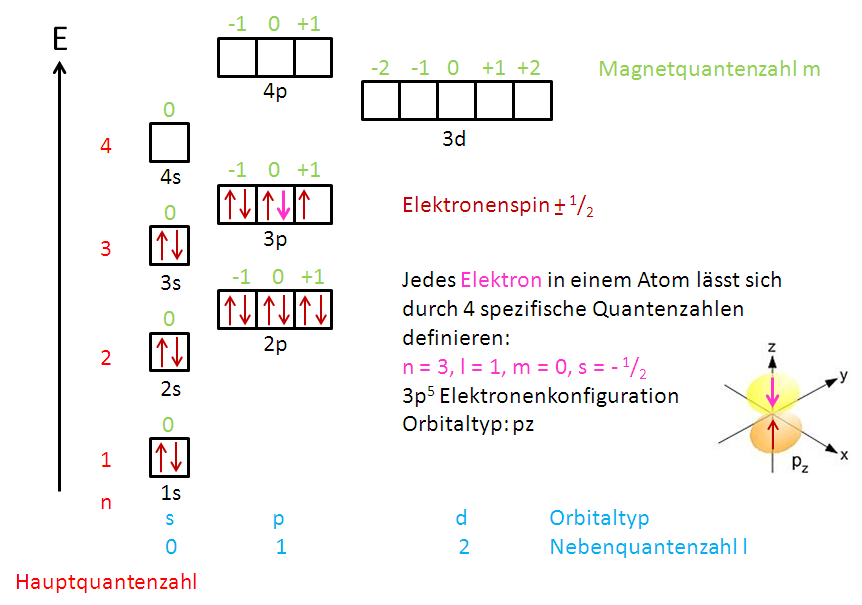
© Belinda Flemming: Energieniveauschema in Zellenschreibweise, CC BY-SA
Es fällt auf, dass die Orbitale nicht in der Reihenfolge steigender Hauptquantenzahlen besetzt werden. So wird z.B. das 4s-Orbital vor dem 3d-Orbital besetzt, da es energetisch günstiger liegt. Das 5s-Orbital wird besetzt, bevor die 4d- und die 4f-Orbitale besetzt werden. Die energetischen Abstände der einzelnen Orbitale bzw. Orbitalgruppen sind idealisiert und entsprechen nicht der Realität.
Bei der Besetzung der Orbitalgruppen treten Unregelmäßigkeiten auf. So wird bei Chrom das 4s-Orbital nur einfach belegt, dafür ist das 3d-Orbital mit 5 Elektronen besetzt. Beim Kupfer wird ebenfalls das 4s-Orbital einfach besetzt, das 3d-Orbital jedoch mit zehn Elektronen. Offenbar weisen Orbitalgruppen, deren Orbitale je einfach besetzt sind, und voll besetzte Orbitalgruppen besondere Stabilität auf.
Um die Reihenfolge der Orbitale im Energieniveauschema über das 4d-Orbital hinaus bestimmen zu können, bedient man sich des folgenden Hilfsmittels. In der folgenden Übersicht ergibt sich die Reihenfolge der zu besetzenden Orbitale nach zunehmender Energie in Pfeilrichtung.

Von Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird Bono~commonswiki als Autor angenommen (basierend auf den Rechteinhaber-Angaben)., CC BY-SA 3.0, Link
Faustregel: Besetzungsreihenfolge entlang der roten Pfeile (Ausnahmen siehe Orbitalblöcke)
Die Elektronenkonfiguration
Außer der Zellenschreibweise gibt es eine weitere Darstellungsmöglichkeit für die Elektronenkonfiguration eines Atoms. Man gibt dabei die Orbitalarten in der Reihenfolge zunehmender Energie (also in der Reihenfolge, in der die Orbitale im Energieniveauschema von unten nach oben auftreten) an und drückt die Elektronenzahl pro Orbitalgruppe durch eine Hochzahl aus. Beispiel: Elektronenkonfiguration des Elements Zinn (50Sn)
Die Ordnungszahl 50 gibt gleichzeitig die Protonenzahl und die Elektronenzahl an:
1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10, 4p6, 5s2, 4d10, 5p2
Die Summe der Hochzahlen ergibt also 50.
