Windenergie
Bei Windkraftanlagen ist eine wichtige Kennzahl die Nennleistung, die angibt, wie viel elektrische Leistung erzeugt wird, wenn die Windgeschwindigkeit an den Rotoren den optimalen Wert besitzt. Der Wert für diese Nenngeschwindigkeit beträgt bei modernen Anlagen \(10\,m/s\) bis \(15\,m/s\). Je nach Standort wird nur in knapp \(20\,\%\) der Zeit dieser Wert erreicht. Oft weht ein sehr viel schwächerer Wind oder der Wind ist zu stark, was dazu führt, dass die Rotoren aus dem Wind gedreht werden müssen, um eine Beschädigung der Anlage zu vermeiden. Grundsätzlich stellt sich die Frage, wie die elektrische Leistung von der Windgeschwindigkeit \(v_{Wind}\) an den Rotoren abhängt.
Innerhalb einer bestimmten Zeitspanne strömt durch die Rotoren Luft mit einer kinetischen Energie \(E_{kin}\), die sich aus der Dichte der Luft \(ρ_{Luft}\) und dem Volumen \(V_{Zylinder}\) des in der Abbildung unten eingezeichneten Luft-Zylinders und der Windgeschwindigkeit \(v_{Wind}\) berechnet:
\(E_{kin} = \frac{1}{2} \cdot m\cdot v_{Wind}^{2} = \frac{1}{2} \cdot ρ_{Luft} \cdot V_{Zylinder} \cdot v_{Wind}^{2} = \frac{1}{2} \cdot ρ_{Luft} \cdot A \cdot b \cdot v_{Wind}^{2}\)
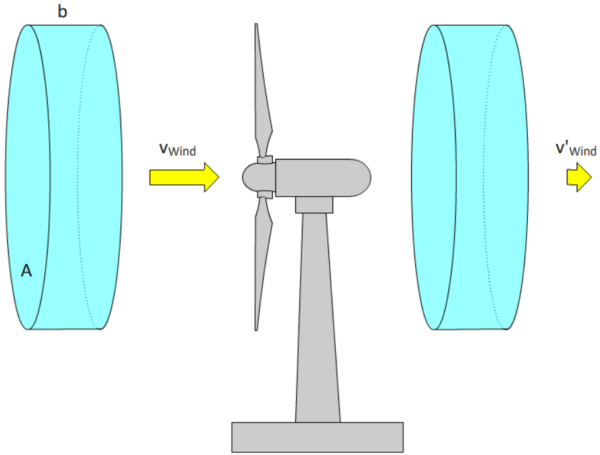
Abbildung: Leistungsberechnung einer Windanlage
Innerhalb der Zeitspanne \(Δt\) berechnet sich die Breite des Zylinders \(b\) zu:
\(b = v_{Wind} \cdot Δt\)
\(E_{kin} = \frac{1}{2} \cdot ρ_{Luft} \cdot A \cdot Δt \cdot v_{Wind}^3\)
Für die mechanische Leistung \(P\) der durch den Rotor strömenden Luftmasse (die Restwindenergie durch \(v_{Wind}^{‚}\) wird vernachlässigt) ergibt sich dann:
\(P = \frac{ΔE_{kin}}{Δt} = \frac{1}{2} \cdot ρ_{Luft} \cdot A \cdot v_{Wind}^3\)
Die Leistung einer Windanlage ist also proportional zur dritten Potenz von \(v_{Wind}\), das bedeutet, eine Halbierung der Windgeschwindigkeit führt dazu, dass die Leistung auf ein Achtel des Ausgangswertes sinkt. Wie eben gezeigt, ist die Ursache dafür, dass sich die kinetische Energie der durchströmenden Luftmasse bei der Halbierung der Windgeschwindigkeit viertelt und gleichzeitig der Durchsatz an Luft durch die Rotoren halbiert. Dieser Umstand sorgt im Zusammenhang mit dem unstetig wehenden Wind dafür, dass die mittlere Leistung einer Windanlage über das Jahr hinweg nur etwa ein Fünftel der Nennleistung beträgt. Möchte man also ausrechnen, wie viele Windräder ein Atomkraftwerk bezüglich der Stromproduktion ersetzen, muss man die Leistung des Atomkraftwerks durch die Nennleistung des Windrads teilen und anschließend mit dem Faktor \(5\) multiplizieren. Für einen Block eines Atomkraftwerks mit einer Leistung von \(1400\,MW\) benötigt man so ca. \(3500\) Windkraftanlagen mit einer heute gängigen Nennleistung von \(2\,MW\). Auch muss man für die Phasen, in denen wenig oder kein Wind weht (im Mittel ca. \(80\,\%\) der Zeit), Kraftwerke zur Verfügung stellen, welche dann rasch die fehlende Leistung liefern. Hier setzt man in Deutschland vor allem auf fossile Gaskraftwerke. Das Einsparungspotential von fossilen Energieträger durch den Einsatz von Windenergie liegt deshalb bei dieser Konstellation nur bei etwa \(20\,\%\).
Den Durchmesser eines Windrades bei gegebener Nennleistung kann man berechnen, wenn man den Wirkungsgrad der Windanlage kennt. Moderne Windkraftanlagen besitzen Wirkungsgrade \(η\) zwischen \(30\,\%\) und \(50\,\%\), wobei der maximale theoretisch erreichbare Wert bei \(60\,\%\) liegt:
\(P_{nutz} = η \cdot \frac{1}{2} \cdot ρ_{Luft} \cdot A \cdot v_{Wind}^3 = η \cdot \frac{1}{2} \cdot ρ_{Luft} \cdot \frac{D^2}{4} \cdot π\cdot v_{Wind}^3\)
\(D = \sqrt{\frac{8 \cdot P_{nutz}}{η \cdot ρ_{Luft} \cdot π \cdot v_{Wind}^3}}\)
Eine Windkraftanlage mit \(2\,Megawatt\) an Nennleistung, einer Nenngeschwindigkeit von \(12\,m/s\) und einem Wirkungsgrad von \(40\,\%\) benötigt damit einen Rotordurchmesser \(D\) von \(78\,m\):
\(D = \sqrt{\frac{8 \cdot 2000000 \ W}{0,40 \cdot 1,2 \ \frac{kg}{m^3} \cdot π \cdot (12 \ \frac{m}{s})^3}} = 78 \ m\)
\([D] = 1 \cdot \sqrt{\frac{W}{\frac{kg}{m^3} \cdot (\frac{m}{s})^3}} = 1 \cdot \sqrt{\frac{Nm}{s} \cdot \frac{m^3}{kg} \cdot \frac{s^3}{m^3}} = 1 \cdot \sqrt{\frac{N \cdot m \cdot s^2}{kg}} = 1 \cdot \sqrt{\frac{kg \cdot m}{s^2}\cdot \frac{m \cdot s^2}{kg}} = 1 \cdot \sqrt{m^2} = 1 \ m\)
Neben dem Vorteil der Einsparung fossiler Energieträger, deren Höhe jedoch auch vom Energiemix abhängt, der bei deren Produktion eingesetzt wurde, existieren auch etliche Nachteile bei der Nutzung von Windenergie. Da eine einzelne Windkraftanlage an Land bis zu \(5000\,m^2\) Fläche benötigen, müssen oft Bäume und andere Pflanzen gerodet werden, was zu einer direkten Zerstörung von Lebensräumen für Tiere und Pflanzen führt. Die erforderlichen Bauarbeiten und das große Fundament können zu einer Bodenverdichtung führen, da schwere Maschinen und Ausrüstung benötigt werden. Die natürliche Wasserdurchlässigkeit wird so reduziert und die regionale Gefahr von Hochwasser steigt. Der Bau vieler Windkraftanlagen an einem Ort zerstört das Landschaftsbild und schadet dem Tourismus in landschaftlich besonders reizvollen Gebieten. Neben Lärmbelästigung auch durch Infraschall, Schattenwurf und Lichtemission gefährden oder töten Windkraftanlagen Vögel, Fledermäuse und Insekten. Die Rotorblätter, die aus kohlenstofffaserverstärktem Kunststoff bestehen sind kaum recycelbar. Ein weiterer negativer Aspekt ist die sogenannte Windabschwächung oder Windverschattung. Die reduzierte Windgeschwindigkeit hinter der Anlage mindert die Effizienz von anderen nahegelegenen Windkraftanlagen. Bei großen Windparks ist es nicht ausgeschlossen, dass das lokale Wettergeschehen beeinflusst wird.
