Ganzrationale Funktionen – Aufgaben

Aufgabe 1: Achsenschnittpunkte

Gegeben sind die folgenden ganzrationalen Funktionen mit Defintionsmenge \(D=\mathrm{I\!R}\). Berechnen Sie die Achsenschnittpunkte der folgenden Funktionen:

a) \(f(x)=x^3+5x^2\)

b) \(g(x)=x^3-2x^2-19x+20\)

c) \(h(x)=0,5x^3-32\)

d) \(i(x)=x^4-4x^2+3\)

e) \(j(x)=x^4+4,5x^3-8,5x^2+3x\)

\(f(0)=0^3+5 \cdot 0^2=0 \Rightarrow S_y (0|0)\)

\(f(x)=0\)

\(x^3+5x^2=x^2(x-5)=0 \Rightarrow x_{1/2}=0, x_3=5\)

\(S_{x1} (0|0), S_{x2} (5|0) \)

\(g(0)=0^3-2 \cdot 0^2-19 \cdot 0+20=20 \Rightarrow S_y (0|20)\)

\(g(x)=0\)

Taschenrechner: \(x_1=1 \)

\(\hphantom{-(}\left(x^3-2x^2-19x+20\right) : \left(x-1\right) = x^2-x-20\\\hphantom{}{{}-\underline{\left(x^3- \hphantom{2} x^2\right)}}\\\hphantom{-\left(\right){}x^{3}:}\color{black}{-x^2}{}- 19x\\\hphantom{-\left(\right){}x^{3}:}\hspace{-16pt}{{}-\underline{\left({}-x^2+\hphantom{19} x\right)}}\\\hphantom{-\left(\right){}x^{3}-x^2+}\color{black}{-20 x}{}+20\\\hphantom{-\left(\right){}x^{3}-x^2+}\hspace{-16pt}{{}-\underline{\left({}-20x{}+20\right)}}\\\hphantom{-\left(\right){}x^{3}-x^2-2x{}{- 4} x+{}}0 \)

\(x^2-x-20=0\)

\(x_{2/3}=\dfrac {-(-1) \pm \sqrt {(-1)^2-4 \cdot 1 \cdot (-20)}} {2 \cdot 1}=\dfrac {1 \pm 9} {2} \)

\(x_2=5, x_3=-4\)

\(S_{x1} (1|0), S_{x2} (5|0), S_{x3} (-4|0) \)

\(h(0)=0,5 \cdot 0^3-32=-32 \Rightarrow S_y(0|-32) \)

\(h(x)=0\)

\(0,5x^3-32=0\)

\(0,5x^3=32\)

\(x^3=64 \Rightarrow x=4\)

\(S_x (4|0) \)

\(i(0)=0^4-4\cdot 0^2+3=3 \Rightarrow S_y (0|3) \)

\(i(x)=0 \)

\(x^4-4x^2+3=0 \)

Substitution: \(x^2=z \)

\( z^2-4z+3=0 \)

\(z_{1/2}=\dfrac {-(-4) \pm \sqrt {(-4)^2-4 \cdot 1 \cdot 3}} {2 \cdot 1}=\dfrac {4 \pm 2}{2}=2 \pm 1 \)

\( z_1=3, ~z_2=1 \)

Resubstitution: \(x=\pm \sqrt z \)

\(x_1= \sqrt {z_1}= \sqrt 3 \Rightarrow S_{x1} (\sqrt 3|0) \)

\(x_2= -\sqrt {z_1}= -\sqrt 3 \Rightarrow S_{x2} (-\sqrt 3|0) \)

\(x_3= \sqrt {z_2}= \sqrt 1=1 \Rightarrow S_{x3} (1|0) \)

\(x_4= -\sqrt {z_2}= -\sqrt 1=-1 \Rightarrow S_{x4} (-1|0) \)

\(j(0)=0^4+4,5 \cdot 0^3-8,5 \cdot 0^2+3 \cdot 0=0 \Rightarrow S_y (0|0)\)

\(j(x)=0\)

\(x^4+4,5 x^3-8,5 x^2+3x=x \left(x^3+4,5 x^2-8,5 x+3 \right)=0 \Rightarrow x_1=0 \)

Taschenrechner: \(x_2=1 \)

\(\hphantom{-(}\left(x^3+4,5x^2-8,5x+3\right) : \left(x-1\right) = x^2+5,5x-3\\\hphantom{}{{}-\underline{\left(x^3- \hphantom{4,5} x^2\right)}}\\\hphantom{-\left(\right){}x^{3}-:}\color{black}{5,5 x^2}{}- 8,5x\\\hphantom{-\left(\right){}x^{3}-:}\hspace{-16pt}{{}-\underline{\left({}5,5x^2-5,5x\right)}}\\\hphantom{-\left(\right){}x^{3}-5,5x^2+:}\color{black}{-3 x}{}+3\\\hphantom{-\left(\right){}x^{3}-5,5x^2+:}\hspace{-16pt}{{}-\underline{\left({}-3x{}+3\right)}}\\\hphantom{-\left(\right){}x^{3}-x^2-2x{}{- 4} x+{}+.}0 \)

\(x^2+5,5x-3=0\)

\(x_{3/4}=\dfrac {-5,5 \pm \sqrt {5,5^2-4 \cdot 1 \cdot (-3)}} {2 \cdot 1}=\dfrac {-5,5 \pm 6,5} {2} \)

\(x_3=0,5, x_4=-6\)

\(S_{x1} (0|0), S_{x2} (1|0), S_{x3} (0,5|0), S_{x4} (-6|0) \)

Aufgabe 2: Graphenverlauf

Aufgabe 3: Funktionsterm bestimmen

Gegeben sind die folgenden ganzrationalen Funktionen mit Defintionsmenge \(D=\mathrm{I\!R}\). Außerhalb des dargestellten Bereichs hat jede Funktion keine weitere Nullstelle.

Bestimmen Sie anhand der gegebenen Graphen der Funktionen den jeweiligen Funktionsterm. Verwenden Sie bei abgelesenen Punkten nur ganzzahlige Wert, also wo der Graph durch das Koordinatengitter verläuft.

Setzen Sie die ersten vier Graphen in der Produktform (Linearfaktordarstellung) \(f(x)=a \cdot (x-x_1) \cdot (x-x_2) \cdot …. \) mit den Nullstellen \(x_1, x_2, … \) an. Sofern es sich um eine mehrfache Nullstelle des Graphen handelt, wird diese Vielfachheit als Exponent außerhalb der Klammer angegeben. Der Funktionsterm darf am Ende in der faktorisierten Form stehenbleiben, Sie müssen ihn nicht ausmultiplizieren.

Setzen Sie die beiden letzten Graphen in der allgemeinen Form \(f(x)=a x^n+b x^{n-1}+… \) an. Wählen Sie dafür einen geeigneten Grad \(n\) der Funktion. Zum Berechnen benötigen Sie so viele Punkte, wie der Grad des Polynoms beträgt.

Nullstellen: \(x_1=-3, x_2=0, x_3=2\)

\(f_1(x)=a (x+3)x(x-2) \)

\(P(-2|4)\) einsetzen (wäre auch mit \(P(1|-2)\) möglich):

\(4=a(-2+3)(-2)(-2-2)\)

\(4=8a \Rightarrow a=\frac {1}{2} \)

\(f_1(x)=\frac {1} {2} (x+3)x(x-2) \)

Nullstellen: \(x_1=-3, x_2=0\) doppelt

\(f_2(x)=a (x+3)x^2 \)

\(P(1|-3)\) einsetzen (wäre auch mit \(P(-2|-3)\) möglich):

\(-3=a(1+3)\cdot 1^2\)

\(-3=4a \Rightarrow a=-\frac {3}{4} \)

\(f_2(x)=-\frac {3} {4} (x+3)x^2 \)

Nullstellen: \(x_1=-3, x_2=0\) doppelt, \( x_3=3\)

\(f_3(x)=a (x+3)x^2(x-3) \)

\(P(-2|-2)\) einsetzen (wäre auch mit \(P(2|-2)\) möglich):

\(-2=a(-2+3)(-2)^2(-2-3)\)

\(-2=-20a \Rightarrow a=\frac {1}{10} \)

\(f_3(x)=\frac {1} {10} (x+3)x^2(x-3) \)

Nullstellen: \(x_1=-2, x_2=0, x_3=3\) dreifach

\(f_4(x)=a (x+2)x(x-3)^3 \)

\(P(4|-1)\) einsetzen (wäre auch mit \(P(1|1)\) möglich):

\(-1=a(4+2)\cdot 4 \cdot (4-3)^3\)

\(-1=24a \Rightarrow a=-\frac {1}{24} \)

\(f_4(x)=-\frac {1} {24} (x+2)x(x-3)^3 \)

Ansatz: Funktion vom Grad \(2\), \(f_5(x)=a x^2+b x+c\)

Punkte: \(A(-2|2), B(-1|1), C(2|3)\)

\(A\) einsetzen: \(2=a \cdot (-2)^2+b \cdot (-2)+c\)

\(\hphantom{einsetzen:}\) I \(2=4a-2b+c\Rightarrow \) I´ \( c=2-4a+2b\)

\(B\) einsetzen: \(1=a \cdot (-1)^2+b \cdot (-1)+c\)

\(\hphantom{einsetzen:}\) II \(1=a-b+c\)

\(C\) einsetzen: \(3=a \cdot 2^2+b \cdot 2+c \)

\(\hphantom{einsetzen:}\) III \(3=4a+2b+c \)

I´ in III: \(3=4a+2b+2-4a+2b\)

\(\hphantom{I´ in I.} 3=4b+2 \)

\(\hphantom{I´ in I.} 1=4b \Rightarrow \underline {b=\frac {1}{4}} \)

I´ und \(b\) in II: \(1=a-\frac {1}{4} +2-4a+2 \cdot \frac {1}{4} \)

\(\hphantom{I´ und b in II} 1=-3a+ \frac{9}{4} \)

\(\hphantom{I´ und b in I.} -\frac {5}{4}=-3a \Rightarrow \underline {a=\frac {5}{12}} \)

\(a\) und \(b\) in I´: \(c=2-4 \cdot \frac {5}{12}+2 \cdot \frac {1}{4}= \underline {\frac {5}{6}} \)

\(f_5(x)=\frac {5}{12} x^2+\frac {1}{4} x+\frac {5}{6} \)

Ansatz: Funktion vom Grad \(3\), \(f_6(x)=a x^3+b x^2+c x+d\)

Punkte: \(A(0|0), B(1|2), C(3|1), D(4|3)\)

\(A\) einsetzen: \(0=a \cdot 0^3+b \cdot 0^2+c \cdot 0+0 \Rightarrow \underline {d=0}\)

\(B\) einsetzen: \(2=a \cdot 1^3+b \cdot 1^2+c \cdot 1\)

\(\hphantom{einsetzen:}\) I \(2=a+b+c \Rightarrow \) I´ \( c=2-a-b\)

\(C\) einsetzen: \(1=a \cdot 3^3+b \cdot 3^2+c \cdot 3 \)

\(\hphantom{einsetzen:}\) II \(1=27a+9b+3c \)

\(D\) einsetzen: \(3=a \cdot 4^3+b \cdot 4^2+c \cdot 4 \)

\(\hphantom{einsetzen:}\) III \(3=64a+16b+4c \)

I´ in II: \(1=27a+9b+3 \cdot (2-a-b)\)

\(\hphantom{I´ in ..} 1=27a+9b+6-3a-3b \)

\(\hphantom{I´ in ..} 1=24a+6b+6 \)

\(\hphantom{I´ in .} -5=24a+6b \Rightarrow\) II´ \(b=\frac {-5-24a}{6} \)

I´ in III: \(3=64a+16b+4 \cdot (2-a-b)\)

\(\hphantom{I´ in I.} 3=64a+16b+8-4a-4b \)

\(\hphantom{I´ in I.} 3=60a+12b+8 \)

\(\hphantom{I´ in I.} -5=60a+12b \)

II´ in III: \( -5=60a+12 \cdot \frac {-5-24a} {6} \)

\(\hphantom{II´in .} -5=60a+2 \cdot (-5-24a) \)

\(\hphantom{II´in .} -5=60a-10-48a \)

\(\hphantom{II´in ..}5=12a \Rightarrow \underline {a=\frac {5}{12}} \)

\(a\) in II´: \(  b=\frac {-5-24\cdot \frac {5}{12}} {6}= \underline {-\frac {5}{2}} \)

\(a\) und \(b\) in I´: \( c=2-\frac {5}{12}- \left( -\frac {5}{2} \right)= \underline {\frac {49}{12}} \)

\(f_6(x)=\frac {5}{12} x^3-\frac {5}{2} x^2+\frac {49}{12} x \)

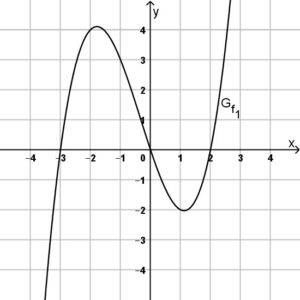
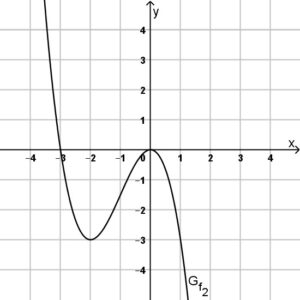
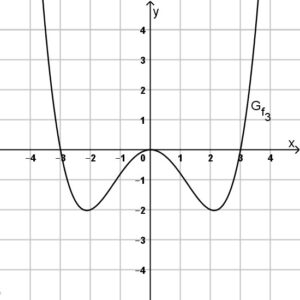
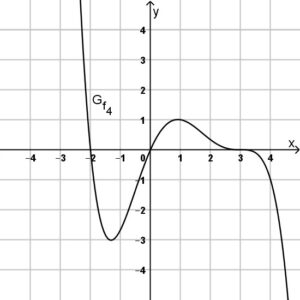
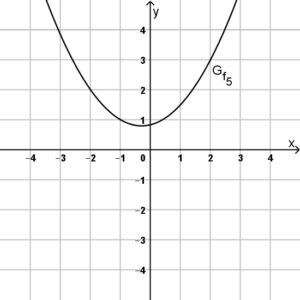
Aufgabe 4: Graphenschnittpunkte

Gegeben sind die folgenden ganzrationalen Funktionen mit Defintionsmenge \(D=\mathrm{I\!R}\). Berechnen Sie die Schnittpunkte der folgenden Funktionen:

a) \(f_1(x)=2x^3+10, g_1(x)=13x^2-13x\)

b) \(f_2(x)=5x^3-x^2, g_2(x)=2x^3-13x^2\)

c) \(f_3(x)=x^4+5x^2, g_3(x)=5x^2+27x\)

\(f_1(x)=g_1(x)\)

\(2x^3+10=13x^2-13x\)

\(2x^3-13x^2+13x+10=0\)

Taschenrechner: \(x_1=2\)

\(\hphantom{-(}\left(2x^3-13x^2+13x+10\right) : \left(x-2\right) = 2x^2-9x-5\\\hphantom{}{{}-\underline{\left(2x^3-\hphantom{1} 4 x^2\right)}}\\\hphantom{-\left(\right){}2x^{3}:}-9x^2+13x\\\hphantom{-\left(\right){}2x^{3}:}\hspace{-16pt}{{}-\underline{\left({}-9x^2+18x\right)}}\\\hphantom{-\left(\right){}2x^{3}9-x^2+.}\color{black}-5x+10\\\hphantom{-\left(\right){}2x^{3}-9x^2+.}\hspace{-16pt}{{}-\underline{\left({}-5x+10\right)}}\\\hphantom{-\left(\right){}2x^{3}-9x^2-5x{}{- 4} x..{}}0 \)

\(2x^2-9x-5=0\)

\(x_{2/3}=\dfrac {-(-9) \pm \sqrt{(-9)^2-4 \cdot 2 \cdot (-5)}} {2 \cdot 2}=\dfrac {9 \pm 11}{4} \)

\(x_2=5, x_3=-0,5\)

\(f_1(x_1)=2 \cdot 2^3+10=26 \Rightarrow S_1 (2|26)\)

\(f_1(x_2)=2 \cdot 5^3+10=260 \Rightarrow S_2 (5|260)\)

\(f_1(x_3)=2 \cdot (-0,5)^3+10=9,75 \Rightarrow S_3 (-0,5|9,75)\)

\(f_2(x)=g_2(x)\)

\(5x^3-x^2=2x^3-13x^2\)

\(3x^3+12x^2=3x^2(x+4)=0\Rightarrow x_1=0, x_2=-4\)

\(f_2(x_1)=5 \cdot 0^3-0^2=0 \Rightarrow S_1 (0|0)\)

\(f_2(x_2)=5 \cdot (-4)^3-(-4)^2=-336\Rightarrow S_2 (-4|-336)\)

\(f_3(x)=g_3(x)\)

\(x^4+5x^2=5x^2+27x\)

\(x^4-27x=x(x^3-27)=0\Rightarrow x_1=0\)

\(x^3-27=0\)

\(x^3=27 \Rightarrow x_2=3\)

\(f_3(x_1)=0^4+5 \cdot 0^2=0 \Rightarrow S_1 (0|0)\)

\(f_3(x_2)=3^4+5 \cdot 3^2=126 \Rightarrow S_2 (3|126)\)

Aufgabe 5: Anwendungsaufgabe

nach Fachabitur 2019, Teil 2, A II, Nr. 1

Das Landesamt für Umwelt ist unter anderem dafür zuständig, vor Überflutungen durch Flüsse zu warnen und lässt dazu täglich kontinuierlich die Wasserstände diverser Flüsse überprüfen.

Der Wasserstand eines bestimmten Flusses im März des Jahres 2010 kann vereinfacht durch die Funktion \(w\) mit der Funktionsgleichung \(w(t)=a t^4+b t^3+c\) mit geeigneten Werten \(a,b,c \in \mathrm{I\!R} \) und der Definitionsmenge \(D_w=[0;30] \) beschrieben werden.

Dabei bedeutet die Variable \(t\) die Zeit in Tagen ab Monatsbeginn zum Zeitpunkt \(t_0=0\). Der Funktionswert \(w(t)\) gibt den Wasserstand des Flusses in cm an.

Zu Monatsbeginn lag der Wasserstand bei 200 cm und am Monatsende bei 308 cm. Der bisherige Hochwasserrekord mit einer Höhe von 420 cm wurde zum ersten mal am 21. März – also zum Zeitpunkt \(t=20\) – erreicht. Der abgebildete Graph zeigt den Wasserstand \(w(t)\) in Abhängigkeit von der Zeit \(t\). Auf das Mitführen von Einheiten bei der Rechnung kann verzichtet werden. Runden Sie Ihre Ergebnisse – falls nicht anders gefordert – sinnvoll.

a) Bestimmen Sie die Werte der Parameter \(a\), \(b\) und \(c\) und damit zu gehörige Funktionsgleichung \(w(t)\).

\(\hphantom{a) }\) Mögliches Ergebnis: \(w(t)=\frac {1}{20\hphantom{.}000} \left( -47 t^4+1490 t^3+4\hphantom{.}000\hphantom{.}000 \right) \)

b) Berechnen Sie die Höhe des Wasserstands zur Monatsmitte in Meter.

c) Während der Wasserstand seit Monatsanfang steigt, breitet sich der Fluss immer weiter hin zu einer Bundesstraße aus. Um diese befahrbar zu halten, wird sie von einem Damm aus Sandsäcken geschützt, welcher gleichmäßig erhöht wird. Die Dammhöhe bezüglich des Wasserstandes lässt sich durch die Funktionsgleichung \( d(t)=2,5 t+226\) beschreiben und gibt die Dammhöhe in cm. Zeigen Sie rechnerisch, dass das Wasser am 11. März auf gleicher Höhe wie der Damm ist, und berechnen Sie, wie hoch der Damm zu diesem Zeitpunkt ist.

Setzen Sie zuerst den Wert beim Monatsanfang in die Funktionsgleichung \(w(t)\) ein, um möglichst einfach die Parameter zu bestimmen.

\(w(t)=a t^4+b t^3+c\)

\(w(0)=200\) einsetzen: \(200=a \cdot 0^4+b \cdot 0^3+c \Rightarrow \underline {c=200}\)

\(w(30)=308\) einsetzen: \(308=a \cdot 30^4+b \cdot 30^3+200\)

\(\hphantom{w()=308 einsetzen:}\) I \(308=810\hphantom{.}000 a+27\hphantom{.}000 b+220\Rightarrow \) I´ \( a=\frac {108-27\hphantom{.}000 b}{810\hphantom{.}000}\)

\(w(20)=420\) einsetzen: \(420=a \cdot 20^4+b \cdot 20^3+200\)

\(\hphantom{w()=420 einsetzenII}\) \(420=160\hphantom{.}000a+8000b+200\)

\(\hphantom{w()=420 einsetzen:}\) II \(220=160\hphantom{.}000a+8000b\)

I´ in II: \(220=160\hphantom{.}000 \cdot \frac {108-27\hphantom{.}000 b}{810\hphantom{.}000}+8000b\)

\(\hphantom{I´ in I} 220=\frac {64}{3}-\frac {16\hphantom{.}000}{3}b+8000b \)

\(\hphantom{I´ in I} 220=\frac {64}{3}+\frac {8000}{3}b \)

\(\hphantom{I´ in I} \frac {596}{3}=\frac {8000}{3}b \Rightarrow \underline {b=\frac {149}{2000}} \)

\(b\) in I´: \(a=\frac {108-27\hphantom{.}000 \cdot \frac {149}{2000}}{810\hphantom{.}000}= \underline {-\frac {47}{20\hphantom{.}000}} \)

\(w(t)=-\frac {47}{20\hphantom{.}000} t^4+\frac {149}{2000} t^3+200 \)

Die Monatsmitte befindet am 16. März, sie liegt also bei \(t = 15\).

Beachten Sie, dass \(w(t)\) die Wasserhöhe in cm angibt und nach m gefragt wird.

\(w(15)=-\frac {47}{20\hphantom{.}000} \cdot 15^4+\frac {149}{2000} \cdot 15^3+200 \approx 332\)

Zur Monatsmitte steht das Wasser ca. 3,32 m hoch.

Berechnen Sie die Schnittstelle der Funktionsterme \(w(t)\) und \(d(t)\), dabei ergibt sich für \(t=10\) eine Schnittstelle, welche dem 11. März entspricht.

Die Höhe des Damms entspricht der Differenz der Höhen zwischen den Zeitpunkten \(t=10\) und \(t=0\).

\(w(t)=d(t)\)

\(-\frac {47}{20\hphantom{.}000} t^4+\frac {149}{2000} t^3+200=2,5t+226 \)

\(-\frac {47}{20\hphantom{.}000} t^4+\frac {149}{2000} t^3-2,5t-26=0 \hphantom{Platz} \bigg \vert \cdot 20\hphantom{.}000 \)

\(-47 t^4+1490 t^3-50\hphantom{.}000 t-520\hphantom{.}000=0 \)

Angabe: \(t_1=10\), entspricht dem 11. März

\(\hphantom{-(}\left(-47 t^4+1490 t^3+\hphantom{10200}0 t^2 -\hphantom{1}50\hphantom{.}000 t-520\hphantom{.}000\right) : \left(t-10\right) = -47t^3+1020 t^2+10\hphantom{.}200t+52\hphantom{.}000\\\hphantom{}{{}-\underline{\left(-47t^4+470t^3\right)}}\\\hphantom{-\left(\right){}-47t^4:}1020t^3+\hphantom{10200}0t^2\\\hphantom{-\left(\right){}-47t^4:}\hspace{-16pt}{{}-\underline{\left({}1020t^3-10\hphantom{.}200t^2\right)}}\\\hphantom{-\left(\right){}-47t^4+470t^3+.}\color{black}10\hphantom{.}200t^2-\hphantom{1}50\hphantom{.}000t\\\hphantom{-\left(\right){}-47t^4+470t^3+.}\hspace{-16pt}{{}-\underline{\left({}10\hphantom{.}200t^2-102\hphantom{.}000t\right)}}\\\hphantom{-\left(\right){}-47t^4+470t^3-10\hphantom{.}200t^2+1}\color{black}52\hphantom{.}200t-520\hphantom{.}000\\\hphantom{-\left(\right){}-47t^4+470t^3-10\hphantom{.}200t^2+1}\hspace{-16pt}{{}-\underline{\left({}52\hphantom{.}000t-520\hphantom{.}000\right)}}\\\hphantom{-\left(\right){}-47 t^4+1490 t^3+\hphantom{10200}0 t^2 -\hphantom{1}50\hphantom{.}000 t-520\hphantom{..}}0 \)

Dammhöhe: \(d(10)-d(0)=2,5 \cdot 10+226-\left(2,5 \cdot 0+226 \right)=25\)

Zurück