Die Linearfaktorform (Nullstellenform)
Neben dem Scheitelpunkt bilden auch die Nullstellen – sofern vorhanden – einen guten Ansatzpunkt, um die Funktionsgleichung zu bestimmen. Neben der allgemeinen und der Scheitelpunktform, gibt es daher noch eine dritte Darstellung für quadratische Funktionen.
Definition: Linearfaktorform
Besitzt eine quadratische Funktion \(f\) die Nullstellen \(x_1\) und \(x_2\), dann gilt:
\[f(x)=a(x-x_1)(x-x_2)\]
Sämtliche Eigenschaften des Leitkoeffizienten \(a\) bleiben wiederum von der allgemeinen Form erhalten.
Die Terme \( (x-x_1) \) sowie \( (x-x_2) \) heißen Linearfaktoren von \(f\).
Der Ursprung der Linearfaktorform liegt im Satz vom Nullprodukt, welcher besagt, dass ein Produkt genau dann den Wert \(0\) besitzt, wenn mindestens einer der beteiligten Faktoren \(0\) ist.
Setzt man nun in die Linearfaktorform von oben beispielsweise \(x_1\) ein, so erhält man
\[f(x_1)=a(\underbrace{x_1-x_1}_{=0})(x_1-x_2)=0\]
und \(x_1\) ist tatsächlich eine Nullstelle von \(f\). Analog wird beim Einsetzen von \(x_2\) die zweite Klammer \(0\), das Ergebnis ist ebenfalls erneut \(0\).
Ein Spezialfall ergibt sich, wenn eine Nullstelle den Wert \(0\) besitzt. Dann lautet der zugehörige Linearfaktor \((x-0)\), weshalb im Funktionsterm dann lediglich der Faktor \(x\) auftaucht. Die Funktion \(g\) mit \(g(x)=2x(x-4)\) besitzt also die beiden Nullstellen \(x_1=0\) und \(x_2=4\).
Für de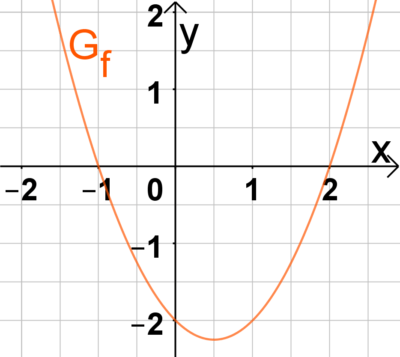
n nebenstehenden Funktionsgraphen liest man als Nullstellen \(x_1=-1\) und \(x_2=2\) ab, weswegen \(f(x)=a(x+1)(x-2)\) gilt. Den Formfaktor \(a\) berechnet man analog zur Scheitelpunktform wiederum aus einem zusätzlichen Graphenpunkt, z.B. \(P(0|-2)\). Einsetzen von \(P\) in \(f(x)\) liefert:
\[\begin{array}\hspace -2&=&a(0+1)(0-2)\\-2&=&a\cdot 1\cdot (-2)\\-2&=&-2a\\1&=&a\end{array}\]
\[\Rightarrow f(x)=(x+1)(x-2)\]
Eine Besonderheit der Linearfaktorform ist, dass diese nur dann existiert, wenn die Funktion \(f\) Nullstellen besitzt – im Gegensatz zur allgemeinen oder Scheitelpunktform die immer existieren.
Ebenso erhält man eine weitere Besonderheit, wenn beide Nullstellen gleich sind, also \(x_1=x_2\) gilt. Es folgt dann
\[f(x)=a(x-x_1)(x-x_2)=a(x-x_1)^2.\]
In diesem Fall ist die Linearfaktorform identisch zur Scheitelpunktform. Man kann nebenstehend als Scheitel \(S(1|0)\) ablesen.
\[f(x)=a(x-1)^2=a(x-1)(x-1)\]
Für den Leitkoeffizienten \(a\) folgt mit dem Punkt \(P\left(0\middle|-\frac12\right)\), dass \(a=-\frac12\) ergibt und damit folgt
\[f(x)=-\frac12(x-1)^2\]
Da in diesem Fall nur eine einzelne Nullstelle vorhanden ist, diese dafür aber doppelt in der Linearfaktorform auftritt, spricht man hierbei auch von einer doppelten Nullstelle. Im Graphen zeigt sich kein Schnittpunkt, sondern nur ein Berührpunkt mit der \(x\)-Achse.
Aufgabe
Ermitteln Sie anhand der gegebenen Funktionsgleichungen möglichst viele Informationen über die zugehörigen Funktionsgraphen (Öffnungsrichtung und -weite, Nullstellen):
| a. \(f(x)=-\frac13(x-3)(x-1)\) | b. \(g(x)=3,5 (x+1)(x-1)\) |
| c. \(h(x)=(x+2)(x+3)\) | d. \(i(x)=-3(x-2)(x-2)\) |
Aufgabe
Bestimmen Sie zu den gegebenen Graphen jeweils die Linearfaktorform.
