Einfache Maschinen – Übung
Aufgabe 1: Geneigte Ebene
1.0 Auf einer geneigten Ebene der Länge \( l= 9{,}5\: \mathrm{m} \) und der Höhe \( h= 3{,}0\: \mathrm{m} \) liegt ein Körper der Masse \( 8{,}0\: \mathrm{kg} \). Verwenden Sie bei dieser Aufgabe für den Ortsfaktor \(g=9{,}81\:\frac{N}{kg}\).
1.1 Berechnen Sie den Neigungswinkel der Ebene und den Betrag der Hangabtriebskraft.
1.2 Berechnen Sie den Betrag der Normalkraft.
Lösungen
Aufgabe 2: Geneigte Ebene
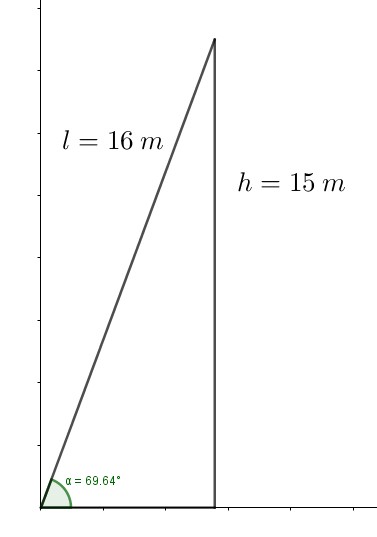
2.0 Ein Schrägaufzug der Länge \(l=16{,}0\:m\) schleift eine Masse von \(m = 980\:kg\) einen Höhenunterschied von \(h = 15{,}0\:m\) hoch.
2.1 Skizzieren Sie zunächst die geneigte Ebene und bestimmen Sie den Neigungswinkel der Ebene.
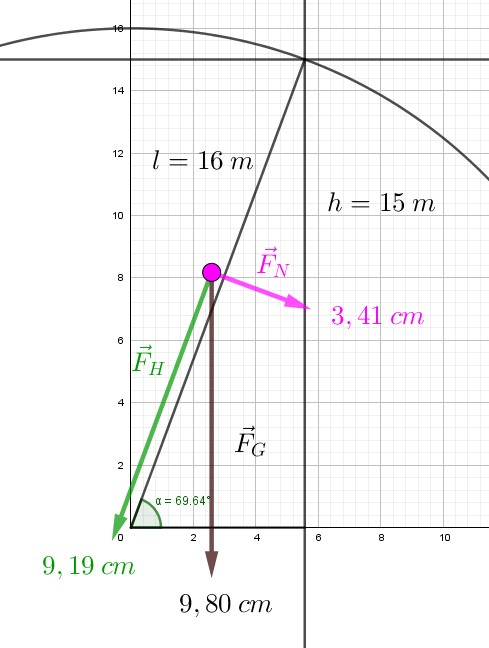
2.2 Berechnen Sie Gewichtskraft, Normalkraft und Hangabtriebskraft. Verwenden Sie \(g=10{,}0\:\frac{N}{kg}\).
2.3 Zeichnen Sie Ebene und alle Kräfte maßstabsgetreu. Bestimmen Sie so Normalkraft und Hangabtriebskraft zeichnerisch.
2.4 Berechnen Sie die Arbeit, die beim Heraufziehen der Masse verrichtet wird, wenn die Reibungskraft vernachlässigt wird.
2.5 Berechnen Sie die Arbeit, die beim Heraufziehen der Masse verrichtet wird, wenn die Reibungszahl \(\mu=0{,}180\) beträgt. Vergleichen Sie dies mit dem direkten Hochheben.
Lösungen
\(sin(\alpha)=\frac{h}{l}\)
\(\alpha=sin^{-1}(\frac{15\:m}{16\:m})\approx 69{,}64^{\circ}\)
\(F_G=m \cdot g=980\:kg \cdot 10{,}0\:\frac{N}{kg}=9800\:N=9{,}80\:kN\)
\(F_N=m \cdot g \cdot cos(\alpha)=980\:kg \cdot 10{,}0\:\frac{N}{kg} \cdot cos(69{,}64^{\circ})=3409{,}59\:N\approx 3{,}41\:kN\)
\(F_H=m \cdot g \cdot sin(\alpha)=980\:kg \cdot 10{,}0\:\frac{N}{kg} \cdot sin(69{,}64^{\circ})=9187{,}75\:N\approx 9{,}19\:kN\)
Der Höhenunterschied wird in der maßstabsgetreuen Zeichnung mit 15 cm Höhe eingetragen.
Für die Gewichtskraft \(F_G=9{,}80\:kN\) wird ein Pfeil der Länge 9,8 cm eingetragen.
Zeichnet man die Kräfte dann korrekt ein, so ergibt sich für die Normalkraft ein Pfeil der Länge 3,41 cm. Dies entspricht \(F_N=3{,}41\:kN\).
Für die Hangabtriebskraft entsteht ein Pfeil der Länge 9,19 cm. Dies entspricht \(F_N=9{,}19\:kN\).
Direkt über die Hubarbeit:
\(W_{Hub}=m \cdot g \cdot h =980\:kg \cdot 10{,}0\:\frac{N}{kg} \cdot 15\:m=147000\:J=147\:kJ\)
Über die geneigte Ebene gilt „Arbeit = Kraft mal Weg“, also „Hangabtriebskraft mal Länge der Ebene“:
\(W=F \cdot s=F_H \cdot l=9{,}19\:kN \cdot 16\:m\approx 147\:kJ\)
Über die geneigte Ebene gilt „Arbeit = Kraft mal Weg“, also „(Hangabtriebskraft+Reibungskraft) mal Länge der Ebene“:
\(W_{geneigt}=F \cdot s=(F_H+F_R) \cdot l\)
\(F_H=9{,}19\:kN\) ist bekannt, die Reibungskraft muss noch ausgerechnet werden:
\(F_R=\mu \cdot F_N=0{,}180 \cdot 3{,}41\:kN=0{,}6138\:kN\approx 0{,}614\:kN\)
\(W_{geneigt}=(F_H+F_R) \cdot l=(9{,}19\:kN+0{,}614\:kN) \cdot 16\:m=156{,}864\:kJ\approx 157\:kJ\)
Dies sind dann also ca. 10 kJ mehr Arbeit als beim direkten hochheben: \(W_{Hub}=147\:kJ\)
Tatsächlich lohnt sich die geneigte Ebene bei dieser Reibungszahl auch nicht mehr zur Kraftersparnis, da mit einer Zugkraft ähnlich der Gewichtskraft zum direkten Hochheben gezogen werden muss:
\(F_{Zug}=(F_H+F_R) =(9{,}19\:kN+0{,}614\:kN)\approx 9{,}80\:kN\)
\(F_G= 9{,}80\:kN\)
Aufgabe 3: Einfacher Flaschenzug
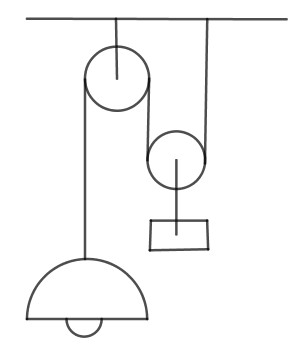
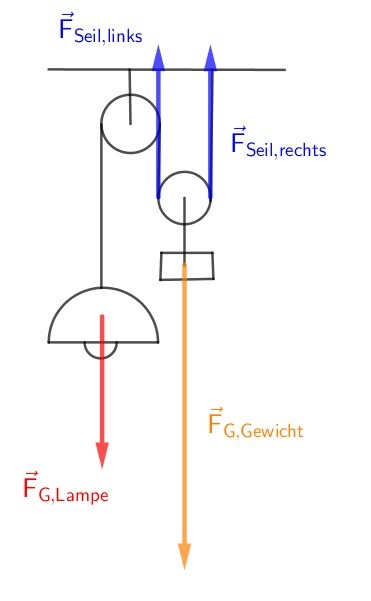
3.0 Eine Esstischlampe hat eine Masse von \(m = 2{,}8\: kg\). Sie hängt am losen Ende eines einfachen Flaschenzugs über dem Tisch, so dass sie in der Höhe verschoben werden kann. An der losen Rolle hängt ein Gegengewicht. Die Masse der losen Rolle wird vernachlässigt.
3.1 Skizzieren Sie die Anordnung. (Falls Sie nicht weiter kommen, machen Sie eine Bildersuche im Internet „Lampe Flaschenzug“.)
3.2 Bestimmen Sie die Masse des Gegengewichts, so dass die Anordnung im Gleichgewicht ist.
3.3 Tragen Sie maßstabsgetreu die Gewichtskraft der Lampe, die Gewichtskraft des Gegengewichts und die Kräfte an den beiden Seilstücken der losen Rolle in Ihre skizzierte Anordnung mit ein. Nutzen Sie für \(F_G\) den Ortsfaktor \(g=10\:\frac{N}{kg}\).
3.4 Sie möchten die Lampe um \(h=34\:cm\) anheben. Geben Sie an, wie viel Arbeit Sie dafür verrichten müssen, wenn die Reibung an den Rollen vernachlässigt wird. Bestimmen Sie, in welche Richtung und wie weit sich dabei das Gegengewicht bewegt.
Lösungen
Die Gewichtskraft des Gegengewichts an der losen Rolle teilt sich je zur Hälfte auf die beiden Seilstücke auf:
Die eine Hälfte hängt an der Decke, während die andere Hälfte über die feste Rolle zur Lampe umgelenkt wird. Für das Gegengewicht ist also die doppelte Masse der Lampe nötig \(m_{Gewicht}=5{,}6\:kg\).
Die Gewichtskraft der Lampe beträgt \(F_{G,Lampe}=m \cdot g=2{,}8\:kg \cdot 10\:\frac{N}{kg}=28\:N\).
Es empfiehlt sich zum Beispiel ein Maßstab von \(28\:N \:\widehat{=} \:5{,}6\:cm\), also \(5\:N \:\widehat{=} \:1\:cm\).
Somit sind \(F_{Seil, links}=F_{Seil, rechts}=28\:N\) (5,6 cm) und \(F_{G, Gewicht}=56\:N\) (11,2 cm):
Wenn die Reibung vernachlässigt wird ist keinerlei Arbeit für das Anheben der Lampe nötig. Die Hubarbeit an der Lampe wird durch das Herabsinken des Gegengewichts ausgeglichen. Somit ist klar: Das Gegengewicht senkt sich ab.
Da das Gegengewicht an zwei Seilen hängt, auf die sich die 34 cm Seillänge aufteilt, senkt sich das Gegengewicht nur um 17 cm ab.
\(W_{Hub, Lampe}=m \cdot g \cdot h=2{,}8\:kg \cdot 10\:\frac{N}{kg} \cdot 0{,}34\:m=9{,}52\:J\approx 9{,}5\:J\)
\(W_{Hub, Gewicht}=m \cdot g \cdot h=5{,}6\:kg \cdot 10\:\frac{N}{kg} \cdot 0{,}17\:m=9{,}52\:J\approx 9{,}5\:J\)
Aufgabe 4: Flaschenzug
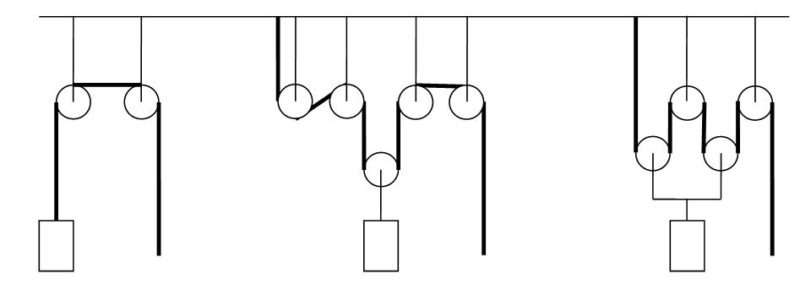
4.0 Unten aufgeführt sind drei Anordnungen von festen und losen Rollen. An allen drei Vorrichtungen hängt jeweils ein Körper der Masse \(m=50\:kg\). Das Gewicht der Rollen und die Reibung des Seils an den Rollen wird bei den folgenden Fragen vernachlässigt.
4.1 Bestimmen Sie die Arbeit, die an allen drei Konstruktionen verrichtet werden muss, um den jeweiligen Körper um die Höhe \(h=10\:m\) anzuheben.
4.2 Geben Sie jeweils an, mit welcher Kraft \(F_{Zug}\) am Seil gezogen werden muss. Geben Sie auch an, wie viele Meter jeweils am Seil gezogen werden muss, um die zehn Meter zusätzliche Höhe für den Körper zu erreichen.
