Komplexe technische Systeme – physikalische Grundlagen II

Maßeinheiten der Atomphysik

Da die üblichen Einheiten für Masse und Energie in der Atom- und Kernphysik zu groß sind, benutzt man hier üblicherweise andere Einheiten.

Masse

Massen gibt man in der atomaren Masseneinheit u an. Dabei legt man fest, dass 1 u der 12. Teil der Masse eines ¹²C-Nuklids ist. Es gilt folgende Umrechnung:

1 u = 1,66·10^-27 kg

Damit ist 1 u etwa die Masse eines Nukleons. Mit Hilfe der Massenspektrografie kann man Massen im atomaren Bereich sehr genau bestimmen. Für die Massen der Teilchen Elektron, Proton und Neutron gilt:

m_e = 0,000549 u; m_p = 1,007276 u;  m_n = 1,008665 u

Energie 

Energien gibt man in eV (Elektronenvolt) an, das ist die Energie, die ein Elektron aufnimmt, wenn es eine Spannungsdifferenz von 1 V durchläuft:

1 eV = 1,6·10^-19 J

Da die üblichen Einheiten für Masse und Energie in der Atom- und Kernphysik zu groß sind, benutzt man hier üblicherweise andere Einheiten.

Masse

Massen gibt man in der atomaren Masseneinheit u an. Dabei legt man fest, dass 1 u der 12. Teil der Masse eines ¹²C-Nuklids ist. Es gilt folgende Umrechnung:

1 u = 1,66·10^-27 kg

Damit ist 1 u etwa die Masse eines Nukleons. Mit Hilfe der Massenspektrografie kann man Massen im atomaren Bereich sehr genau bestimmen. Für die Massen der Teilchen Elektron, Proton und Neutron gilt:

m_e = 0,000549 u; m_p = 1,007276 u;  m_n = 1,008665 u

Energie 

Energien gibt man in eV (Elektronenvolt) an, das ist die Energie, die ein Elektron aufnimmt, wenn es eine Spannungsdifferenz von 1 V durchläuft:

Massendefekt

Betrachtet man einen Heliumkern , der aus zwei Protonen und zwei Neutronen besteht, so sollte man erwarten, dass seine Masse

m = 2 · m_p + 2 · m_n = 2 · 1,007276 u + 2 · 1,008665 u = 4,031882 u

beträgt. Tatsächlich misst man aber eine Nuklidmasse des He von nur

m( ) =  4,001506 u.

Es besteht also die Massendifferenz m = 4,031882 u – 4,001506 u = 0,030376 u. Eine Massendifferenz stellt man bei allen Kernen fest.

Allgemein lässt sich festhalten:

Die Masse eines Nuklids ist stets kleiner als die Summe der Massen seiner Nukleonen. Diese Differenz bezeichnet man als Massendefekt m. Er berechnet sich wie folgt:

m = Z · m_p + N · m_n – m

Dabei bezeichnet m die tatsächliche Masse des Kerns.

Äquivalenz von Masse und Energie 

Eine Deutung des Massendefekts gelingt mit der berühmten Formel Albert Einsteins, die er 1905 im Rahmen der speziellen Relativitätstheorie entwickelte:

Diese Formel besagt, dass Masse und Energie zwei einander äquivalente Größen sind. c² spielt in der Formel nur die Rolle einer Proportionalitätskonstanten. Um zu sehen, welche Energiemenge 1 g Masse entspricht, wird nach der Einstein’schen Formel folgende Umrechnung durchgeführt:

E = m · c² = 1 · 10^-3 kg · (3 · 10⁸ m/s)² = 9 · 10¹³ J

Zur besseren Beurteilung dieser Menge erfolgt noch die Umrechnung in kWh und in t SKE:

E = 9 · 10¹³ J = 2,5 · 10⁷ kWh = 3,1 · 10³ t SKE

In 1 g Masse steckt also die unvorstellbare Menge Energie von ca. 3000 t Steinkohle. Es existiert jedoch keine technische Möglichkeit, mit der diese Energie freigesetzt werden könnte.

Als zweites Beispiel wird hier berechnet, wie viel Energie einer atomaren Masseneinheit u entspricht:

E = m · c² = 1,66 · 10^-27 kg (3 · 10⁸ m/s)² = 1,49 · 10^-10 J

Schließlich wird dieser Wert noch in eV umgerechnet, man erhält:

1 u = 933 MeV

Bindungsenergie

Mit Hilfe der Einstein’schen Formel lässt sich der Massendefekt folgendermaßen deuten: Die beim Zusammenbau eines Kerns aus seinen Nukleonen „verloren gegangene“ Masse, der Massendefekt, wird als Energie freigesetzt, und zwar ist das genau die Bindungsenergie, mit der die Nukleonen im Kern zusammenhalten. Umgekehrt müsste man diese Energie aufwenden, wollte man einen Kern in seine Nukleonen zerlegen.

Als Beispiel wird im Folgenden die Bindungsenergie eines Heliumkerns berechnet. Nach der getroffenen Vorzeichenregel ist Bindungsenergie die beim Zusammenbau eines Kerns abgegebene Energie, sie müsste deshalb mit einem negativen Vorzeichen versehen werden. Zur Vereinfachung wird im Folgenden nur der Betrag der Bindungsenergie betrachtet. Wie oben berechnet, gilt für den Massendefekt eines Heliumkerns:

m = 0,030376 u

Mit dem Zusammenhang, dass 1u = 933 MeV ist, erhält man für die Bindungsenergie E_He = 28,3408 MeV. Zu Vergleichszwecken ist es sinnvoll, die Bindungsenergie pro Nukleon zu bestimmen; beim He-4-Kern bedeutet dies, dass man durch 4 dividiert:

E_B = 7,0852 MeV

So wie für den He-4-Kern dargestellt, kann man für jedes Isotop die Kernbindungsenergie pro Nukleon bestimmen. Trägt man diese Bindungsenergie gegen die Massenzahl A auf, so ergibt sich die nachfolgend dargestellte Kurve.

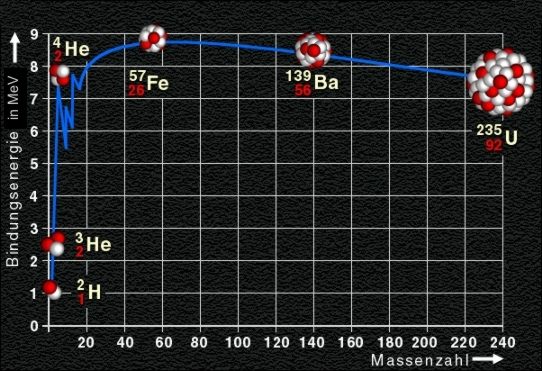
Man teilt die Nuklide in leichte Kerne, mittelschwere und schwere Kerne ein. Die Kurve zeigt demnach, dass die leichten Kerne, mit Ausnahme des He-4-Kerns, eine vergleichsweise niedrige Bindungsenergie aufweisen. Die mittelschweren Kerne zeigen ein Maximum bei der Bindungsenergie, während die schweren Kerne wiederum eine geringere Bindungsenergie besitzen.