Kräftezerlegung und schiefe Ebene
Einführung
Stellen Sie sich eine Geschicklichkeitsübung vor, bei der Sie mit einem Hammer einen Nagel mit einem einzigen Schlag in ein Holzbrett schlagen sollen. Dabei müssen Sie nicht nur die nötige Kraft aufbringen, vielmehr kommt es auch darauf an, den nagel gerade, also in der richtigen Richtung zu treffen.
Kräfte besitzen neben ihrem Betrag immer eine Richtung, sie sind vektorielle Größen. Bei der grafischen Darstellung einer Kraft durch einen Kraftpfeil ist die Länge des Pfeils ein Maß für den Betrag der Kraft, Richtung und Orientierung sind durch den Anfangspunkt und die Spitze des Pfeils festgelegt.
Greifen verschiedene Kräfte an einem Körper an, kann man die Einzelkräfte zu einer Gesamtkraft, der sogenannten Resultierenden, zusammenfassen. Bei dieser Addition muss man jedoch den Vektorcharakter der Kräfte berücksichtigen, d.h. man muss eine Vektoraddition durchführen. Graphisch geschieht dies mit Hilfe eines Parallelogramms.

Für viele Problemstellungen in der Physik ist es nötig, Kräfte zusammenzufassen oder in ihre Einzelkomponenten zu zerlegen.
Kräftezerlegung an der schiefe Ebene
Die schiefe Ebene gilt als eine der ältesten Maschinen der Menschheit. Man nimmt an, dass die Ägypter vor ca. 4000 Jahren große schiefe Ebenen aus Sand aufschütteten um beim Pyramidenbau Steinblöcke nach oben zu befördern.
Will man Beschleunigungs- oder Reibungskräfte an der schiefen ebene berechnen, muss man eine Kräftezerlegung durchführen.
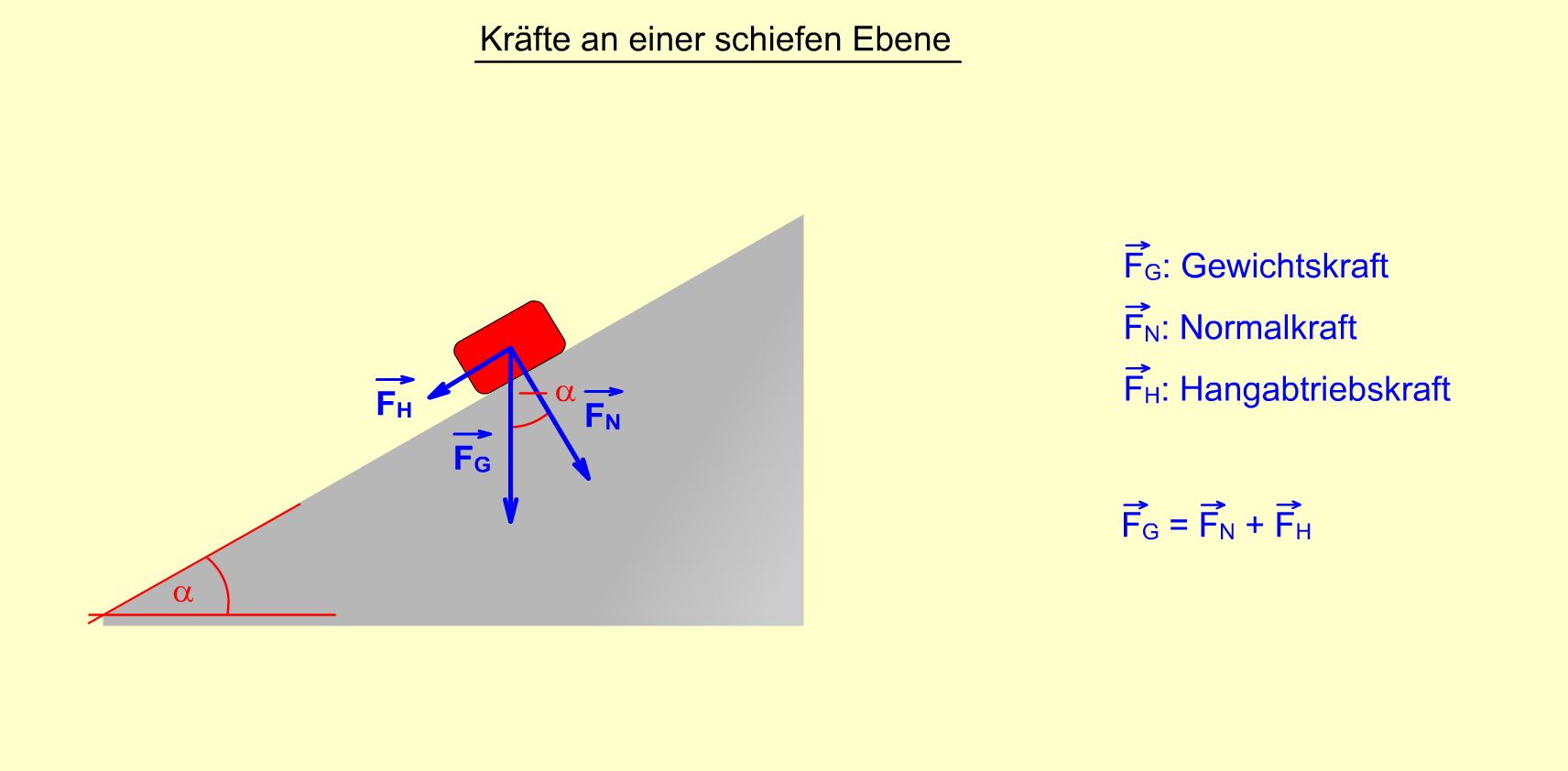
Unabhängig von der Stärke der Neigung der schiefen Ebene greift an einem Körper auf der schiefen Ebene seine Gewichtskraft mit dem Betrag \( F_{\mathrm{G}} = m\cdot g \) an. Die Gewichtskraft ist dabei immer senkrecht nach unten (zum Erdmittelpunkt hin) gerichtet.
Die Gewichtskraft \(\vec{ F_{\mathrm{G}}} \) kann in zwei Komponenten zerlegt werden. Die Komponente \(\vec{ F_{\mathrm{H}}} \) wirkt längs der Oberfläche und sorgt dafür, dass der Körper nach unten gezogen wird. Sie wird Hangabtriebskraft genannt. Die zweite Komponente heißt Normalkraft \(\vec{ F_{\mathrm{N}}} \) und steht senkrecht auf der Oberfläche. Sie gibt an, mit welcher Kraft der Körper auf die schiefe Ebene gedrückt wird und ist notwendig für die Berechnung von auftretenden Reibungskräften.
Der Winkel \( \alpha \), der ein Maß für die Neigung der Ebene ist, tritt auch in dem rechtwinkligen Kräftedreieck auf (siehe oben). Die Beträge der Hangabtriebskraft und der Normalkraft können mit Hilfe der Trigonometrie bestimmt werden:
Hangabtriebskraft: \( F_{\mathrm{H}} = F_{\mathrm{G}} \cdot \sin (\alpha) = m \cdot g \cdot \sin (\alpha) \)
Normalkraft: \( F_{\mathrm{N}} = F_{\mathrm{G}} \cdot \cos (\alpha) = m \cdot g \cdot \cos (\alpha) \)
Für die auftretende Reibungskräfte ist nur die Normalkraft wichtig, da sie die Komponente der Gewichtskraft ist, mit der der Körper senkrecht auf die Fläche gedrückt wird. Haft- bzw. Gleitreibungskraft können folgendermaßen ermittelt werden:
Reibungskraft: \( F_{\mathrm{R}} = \mu \cdot F_{\mathrm{N}} = \mu \cdot F_{\mathrm{G}} \cdot \cos (\alpha) = \mu \cdot m \cdot g \cdot \cos (\alpha) \)
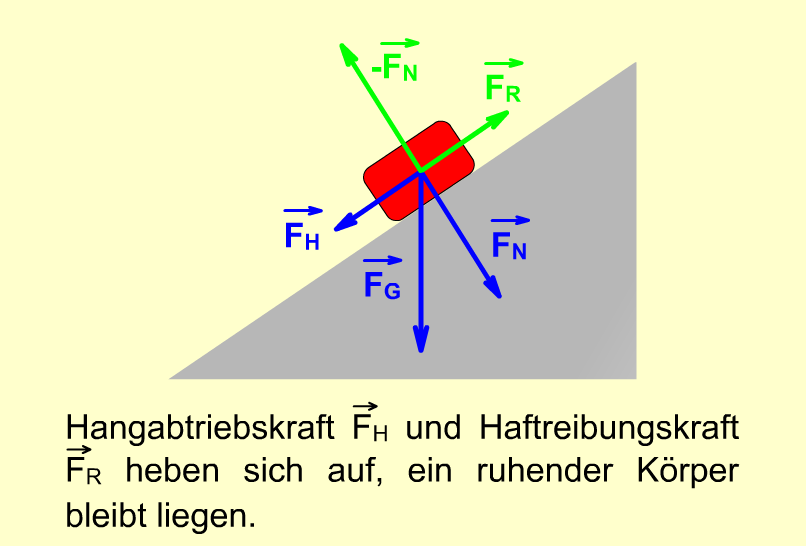
In obiger Zeichnung sind der Übersichtlichkeit halber die Gegenkräfte nicht eingezeichnet. Eine dieser Gegenkräfte ist die entgegengesetzt gerichtete Normalkraft \( – \vec{F_{\mathrm{N}}} \), mit der die schiefe Ebene gegen den Körper drückt (siehe Bilder unten).
Bleibt der Körper auf der schiefen Ebene in Ruhe, heben sich die Hangabtriebskraft \( \vec{F_{\mathrm{H}}} \) und die Haftreibungskraft \( \vec{F_{\mathrm{R}}} \) genau auf (siehe linkes Bild).
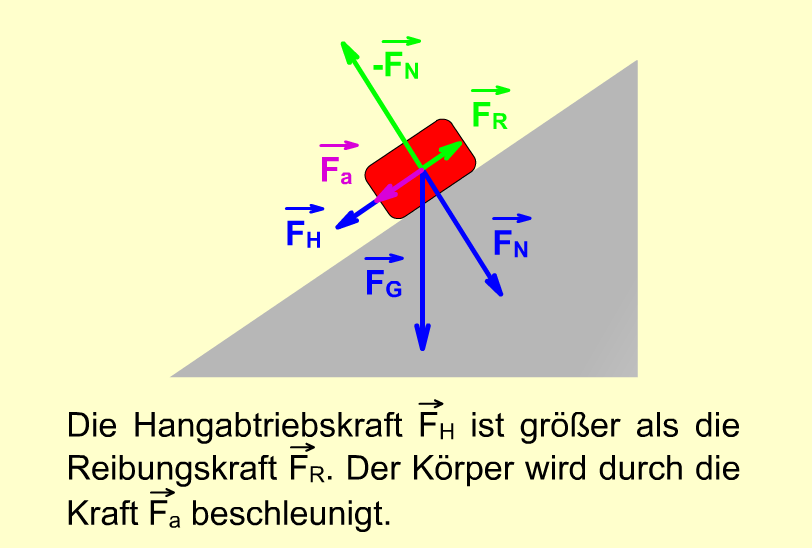
Bei einer genügend steilen Ebene oder glatter Oberfläche kann die Hangabtriebskraft \( \vec{F_{\mathrm{H}}} \) vom Betrag her größer sein als die entgegengesetzte Reibungskraft \( \vec{F_{\mathrm{R}}} \). In diesem Falll wird der Körper mit der Kraft \( \vec{F_{\mathrm{a}}} \) beschleunigt. Der Betrag von \( \vec{F_{\mathrm{a}}} \) berechnet sich aus der Differenz der Kraftbeträge von \( \vec{F_{\mathrm{H}}} \) und \( \vec{F_{\mathrm{R}}} \) (siehe rechtes Bild).