Das Urnenmodell
Ein häufig genutztes Modell ist das sogenannte Urnenmodell. Auf der vorherigen Seite wurde ein solches Urnenmodell schon behandelt, auch wenn der Name noch nicht erwähnt wurde. Das Urnenmodell geht stets von einem Gefäß (Urne) aus, in dem sich Kugeln befinden. Diese Kugeln sind äußerlich identisch (Größe, Material, etc.), so dass ohne das Herausnehmen einer Kugel nicht vorhergesagt werden kann, welche Kugel gezogen wird. Je nachdem wie das Zufallsexperiment abläuft unterscheidet man zwei grundsätzlich unterschiedliche Vorgänge: das Ziehen ohne Zurücklegen (ZoZ) und Ziehen mit Zurücklegen (ZmZ). Wie der Name bereits andeutet unterscheiden die beiden Vorgänge sich darin, ob eine gezogene Kugel zurück in die Urne gelegt wird, bevor der nächste Zug erfolgt oder nicht.
Insbesondere bei Vorgängen, die zu kompliziert sind, um die Ergebnisräume vollständig hinzuschreiben (z.B. Lottospielen mit \(\vert \Omega \vert \approx 140000000 \)), kann das Zurückführen auf das passende Urnenmodell helfen, die Situation zu erfassen. Dies wird in einem späteren Kapitel – der Kombinatorik – noch ausführlich behandelt. Für den Moment sollen zunächst anhand eines einfachen Beispiels das Ziehen mit bzw. ohne Zurücklegen verdeutlicht werden.
In einer Urne befinden sich drei Kugeln, die mit den Ziffern \(1, 2\) bzw. \(3\) beschriftet sind. Es werden nacheinander zwei Kugeln gezogen.
Ziehen ohne Zurücklegen
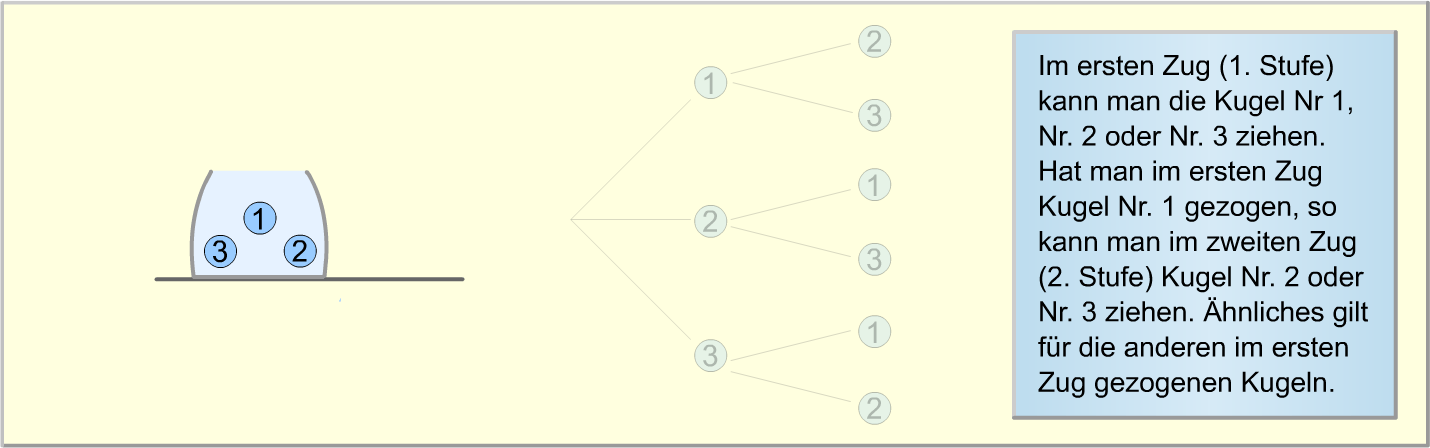
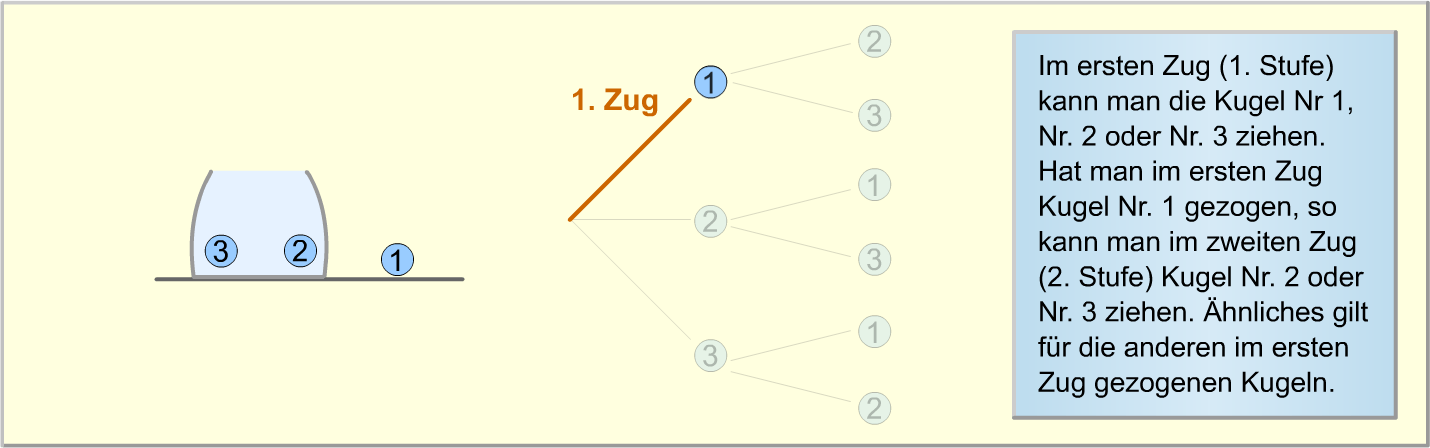
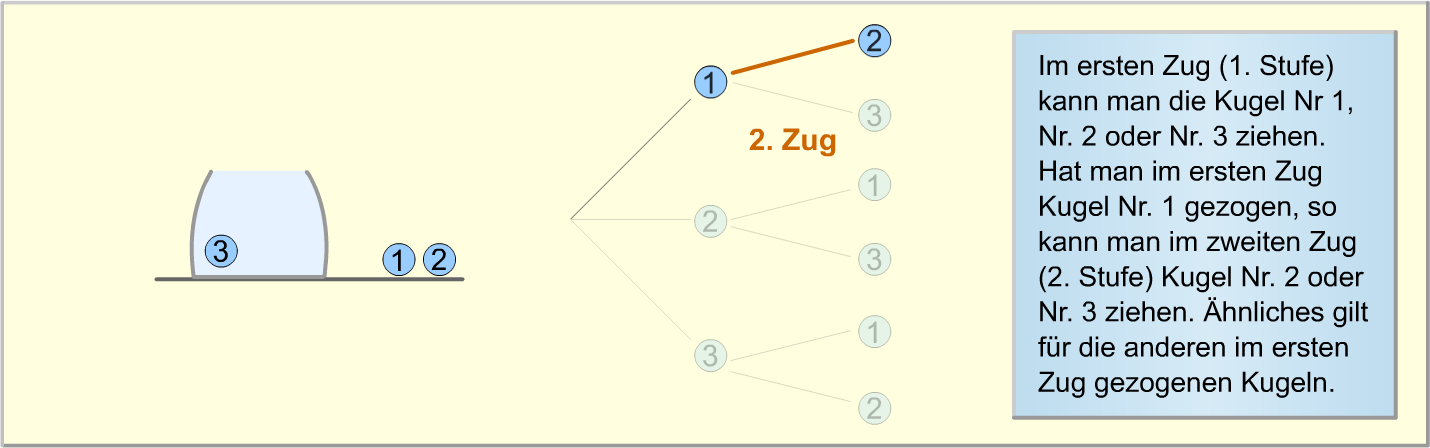
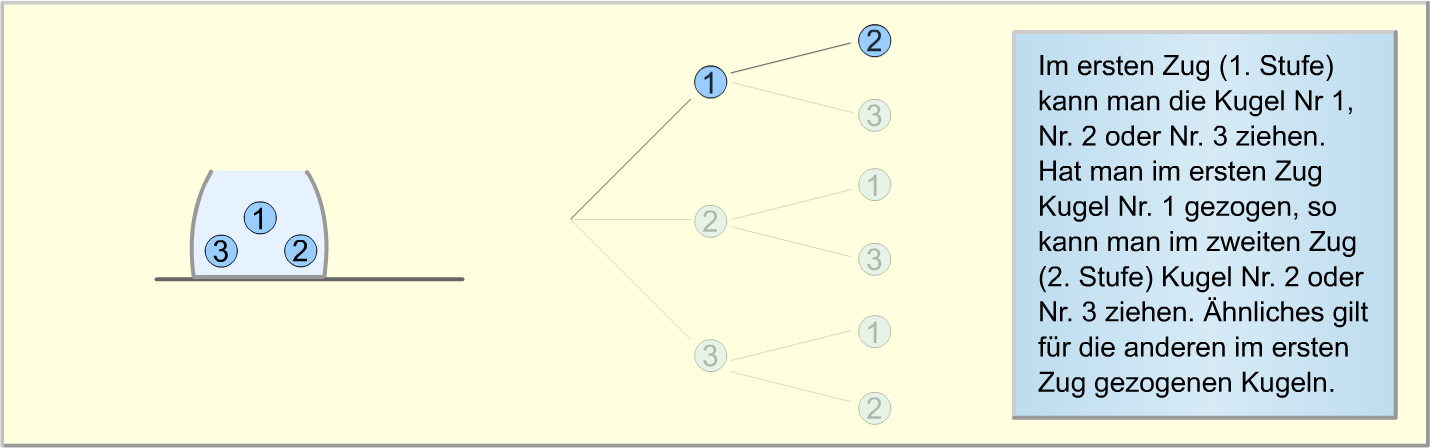
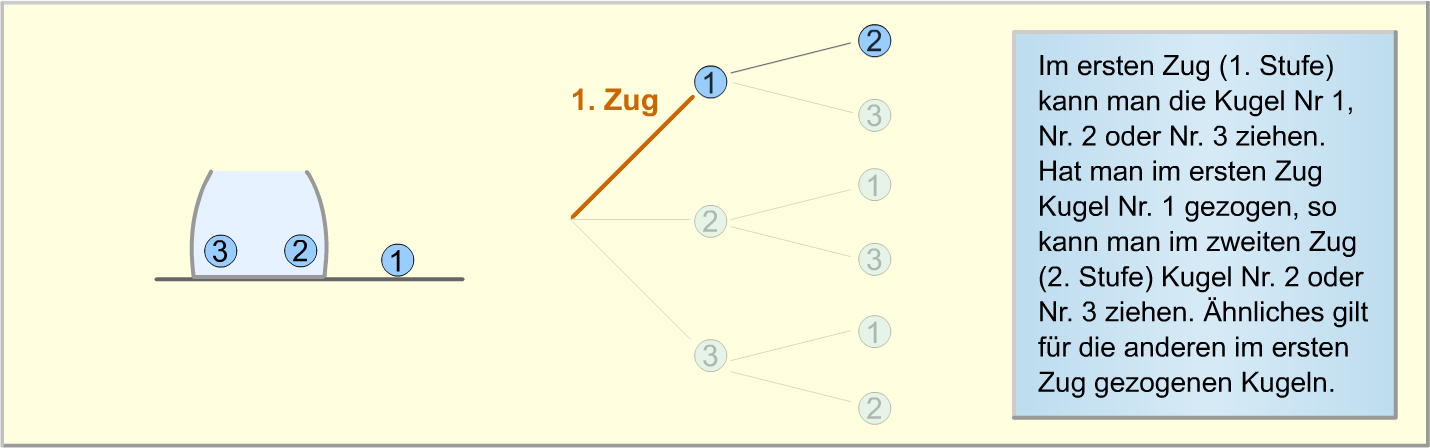
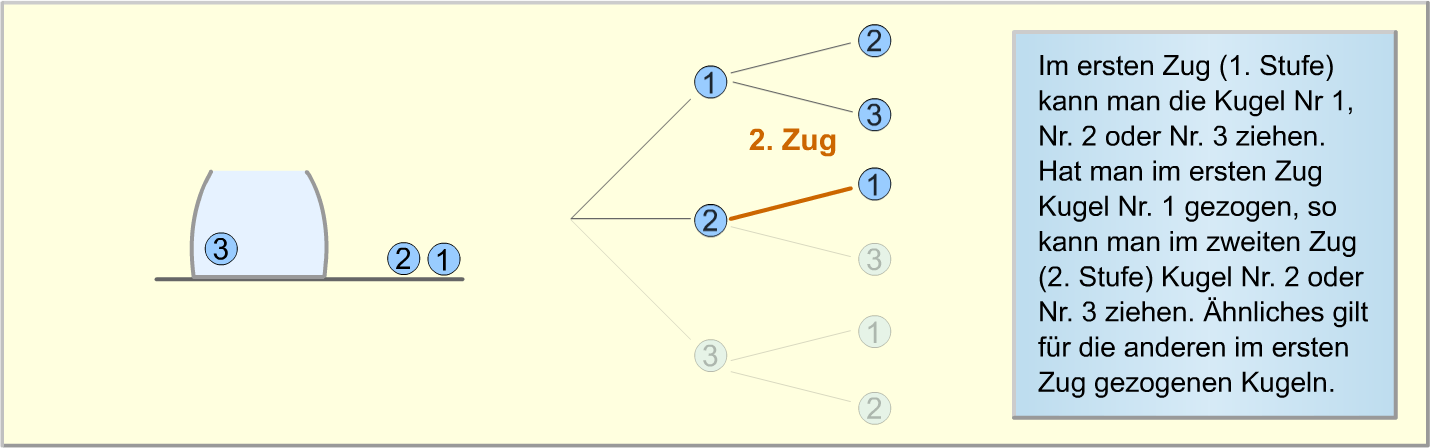
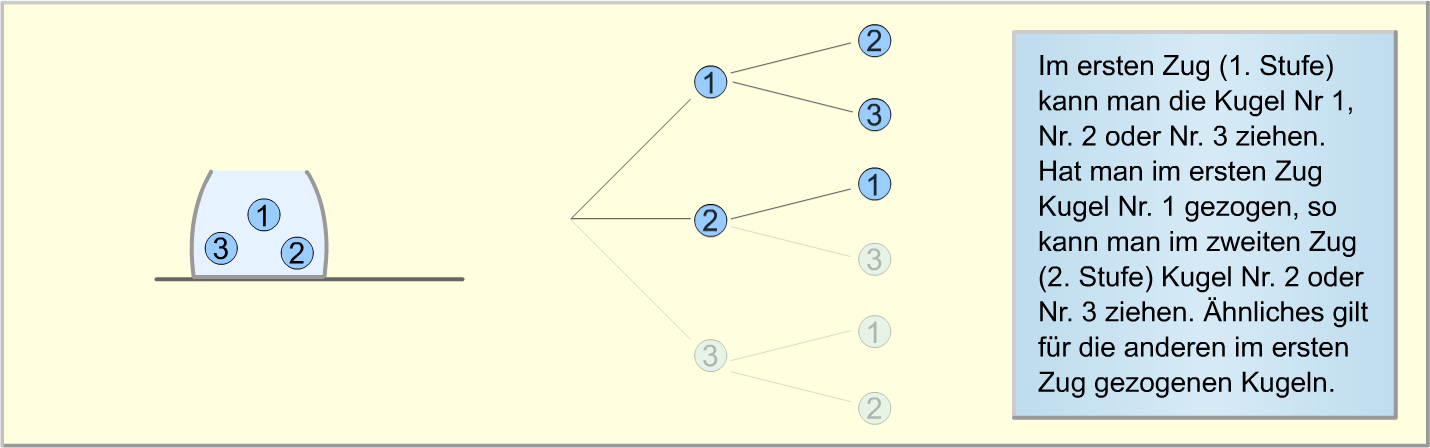
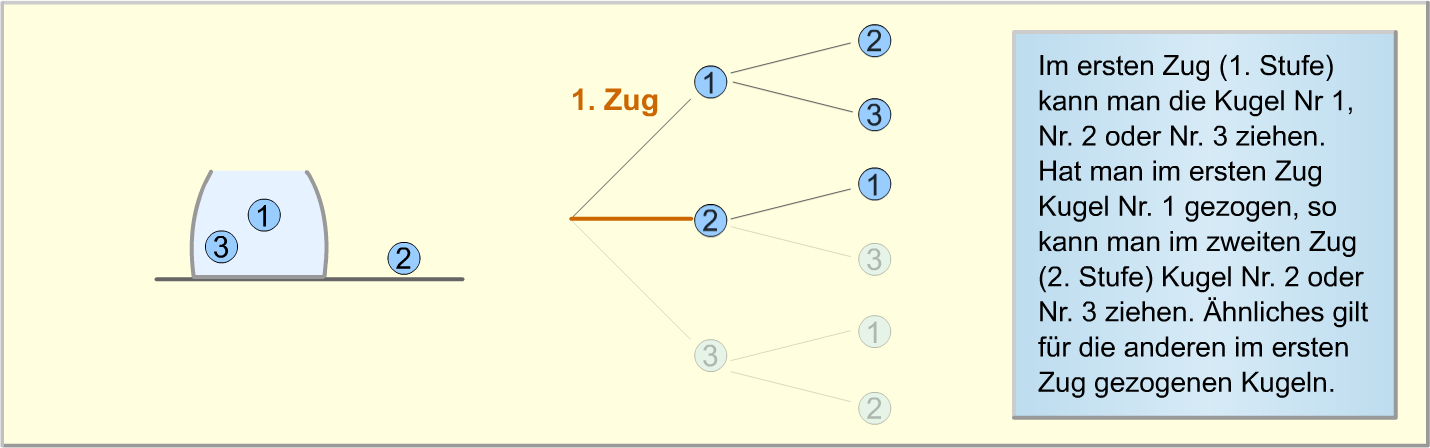
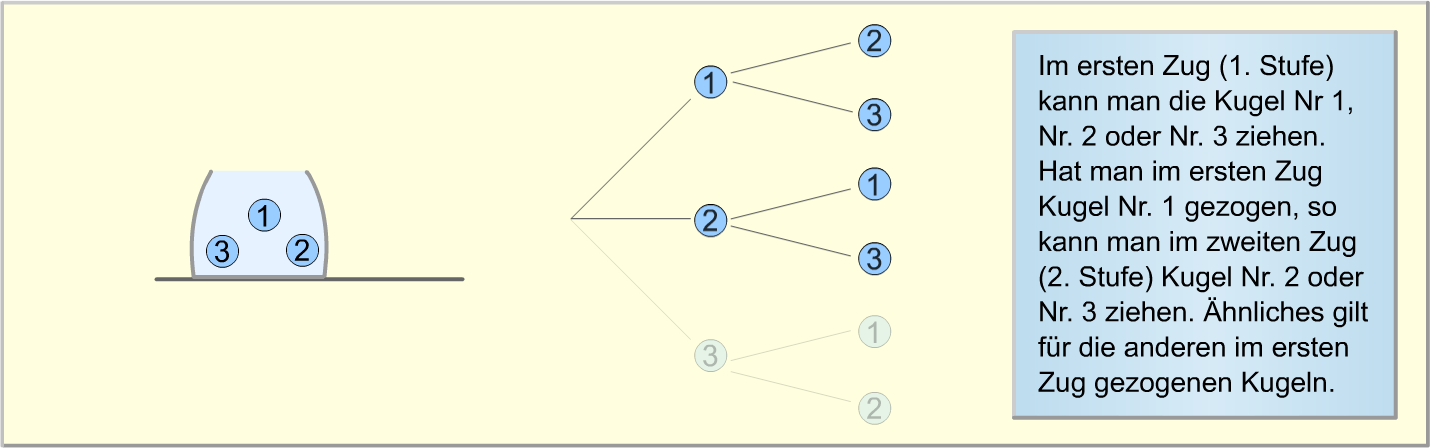
Die folgende Bilderstrecke verdeutlicht erneut, wie das Baumdiagramm zu diesem Zufallsexperiment aufgebaut wird.
Insgesamt besteht das Baumdiagramm damit aus \(6\) Pfaden und die Ergebnisse lauten:
\(\omega_1=(1,2), \omega_2=(1,3), \omega_3=(2,1), \omega_4=(2,3), \omega_5=(3,1), \omega_6=(3,2)\).
Folglich ist der zugehörige Ergebnisraum \(\Omega=\{(1,2);(1,3);(2,1);(2,3);(3,1);(3,2)\}\) und \(\vert \Omega \vert =6\).
Aufgabe
Geben Sie – ausgehend von oben stehendem Baumdiagramm – den Ergebnisraum an, wenn die Reihenfolge der gezogenen Zahlen nicht entscheidend ist. Geben Sie außerdem die Mächtigkeit dieses Ergebnisraums an.
Ziehen mit Zurücklegen
In analoger Weise zu obigem Beispiel kann man auch für das Ziehen mit Zurücklegen ein Baumdiagramm erstellen. Der Unterschied zum Ziehen ohne Zurücklegen besteht offensichtlich darin, dass für den zweiten Zug alle drei Kugeln zur Verfügung stehen. Das vollständige Baumdiagramm sieht also folgendermaßen aus:

Zusätzlich zu den bisherigen Ergebnissen kommen nun also noch drei weitere Ergebnisse hinzu: \((1,1), (2,2)\) und \((3,3)\).
Der neue Ergebnisraum besteht also aus insgesamt \(9\) Ergebnissen (\(\Rightarrow \vert \Omega \vert =9\)), nämlich:
\(\Omega=\{(1,1);(1,2);(1,3);(2,1);(2,2);(2,3);(3,1);(3,2);(3,3)\}\).
Aufgabe
Geben Sie auch hier den Ergebnisraum und seine Mächtigkeit an, wenn die Reihenfolge der gezogenen Kugeln keine Rolle spielt.