Verwendung des Tafelwerks
Aufbau der Tabellen für Wahrscheinlichkeiten in Bernoulli-Ketten
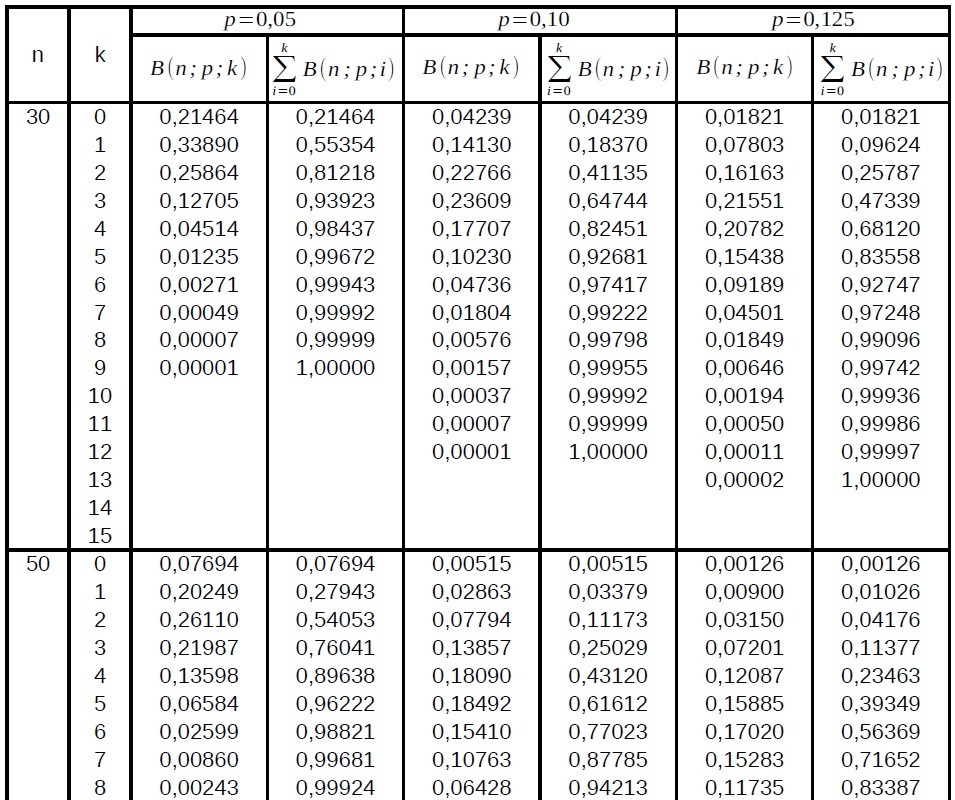
In Tafelwerken zur Stochastik sind Wahrscheinlichkeiten in Bernoulli-Ketten für ausgewählte Trefferwahrscheinlichkeiten \(p\) aufgelistet:
Einzelwahrscheinlichkeiten für genau \(k\) Treffer
aufsummierte (kumulierte) Wahrscheinlichkeiten von \(0\) bis \(k\) Treffer
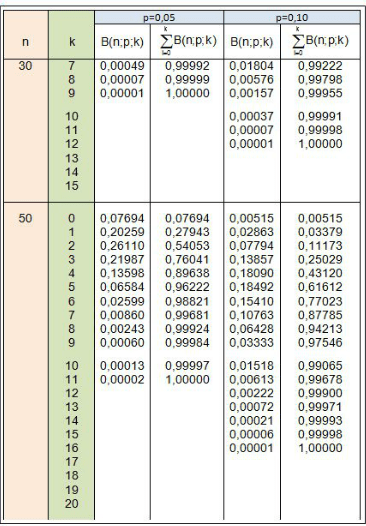
Bedeutung der einzelnen Tabellenbereiche
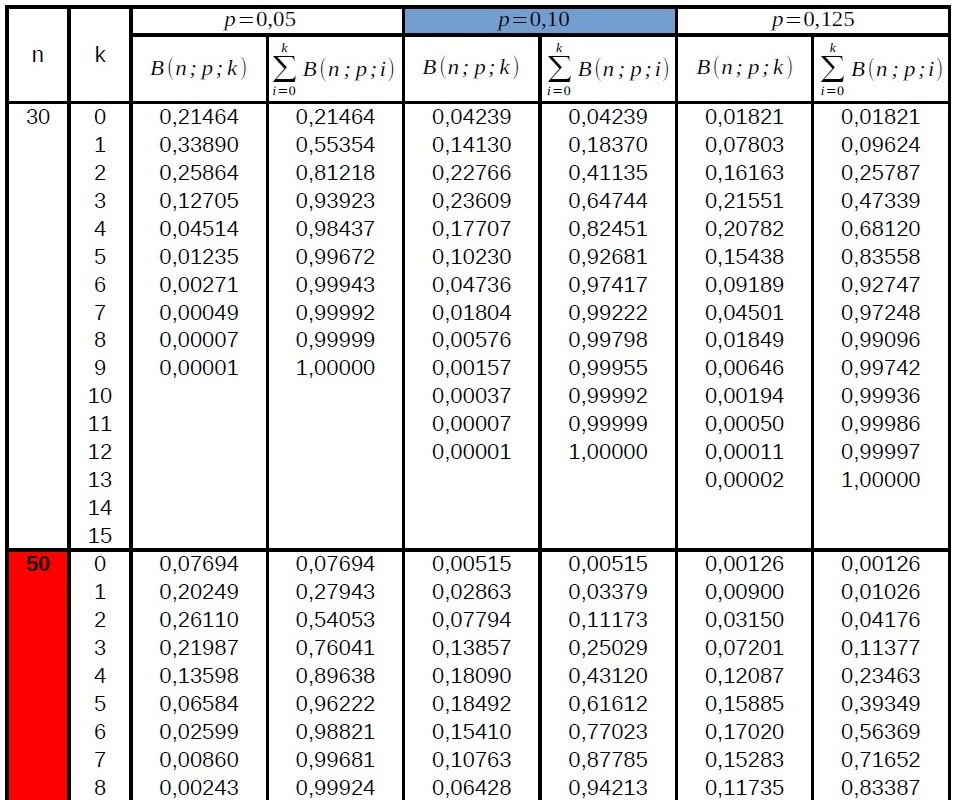
1. Kopfzeile (blau): Trefferwahrscheinlichkeit \(p\)
2. Randspalte (rot): Kettenlänge \(n\)
3. Randspalte (grün): Trefferanzahl \(k\)
Zu jeder Trefferwahrscheinlichkeit (z.B. \(p=0,05\)) gibt es zwei Spalten:
linke Spalte:
Wahrscheinlichkeit für genau \(k\) Treffer \((T)\)
\(P(T=k) = B(n;p;k)\)
rechte Spalte:
aufsummierte (kumulierte) Wahrscheinlichkeit für \(0\) bis \(k\) Treffer \(P(T \leq k) = F_p^n (k) = \sum_{ i=0 } ^k B(n;p;i)\)
Schrittfolge zum Ermitteln von WK mit dem Tafelwerk
1. Suche im Tafelwerk die Seite mit der benötigten Trefferwahrscheinlichkeit \(p\).
2. Gehe dort zur Tabellenzeile mit der benötigten Kettenlänge \(n\).
3. Suche dort die Zeile mit der benötigten Trefferanzahl \(k\).
4. Lies dort den Wert der Wahrscheinlichkeit ab:
a) bei Einzelwahrscheinlichkeiten in der linken Spalte
b) bei aufsummierten Wahrscheinlichkeiten in der rechten Spalte
Die Einzelwahrscheinlichkeiten in der jeweils linkten Spalte können auch mit der Bernoulli-Formel berechnet werden.
Die aufsummierten (kumulierten) Wahrscheinlichkeiten von \(0\) bis \(k\) Treffer können jeweils fertig in der jeweils rechten Spalte abgelesen werden, statt mühsam alle einzelnen Werte zu berechnen und anschließend zu addieren. Für die kumulierte Wahrscheinlichkeit gibt es verschiedene Schreibweisen: \(P(T \leq k) = F_p^n (k) =\) \( \sum_{ i=0 } ^k B(n;p;i)\)
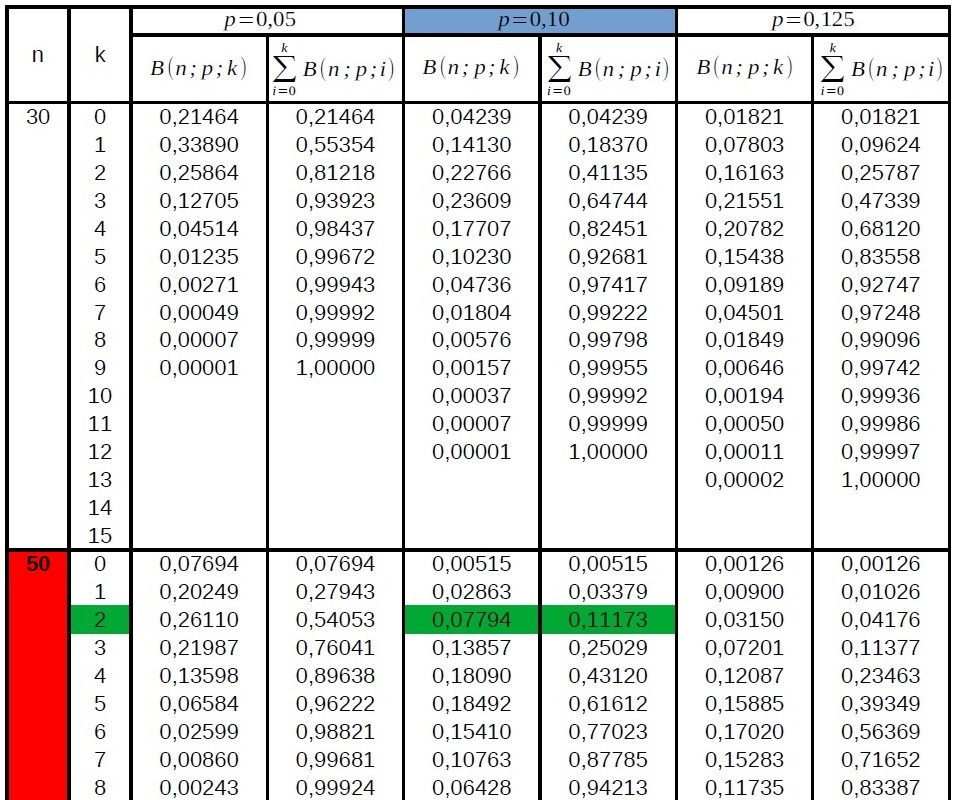
Beispiel für Einzelwahrscheinlichkeit:
gegeben: \(p = 0,10, n = 50\)
gesucht: WK für \(2\) Treffer
Ablesen in der Tabelle im Tafelwerk (linke Spalte): \(P(T=2) = B(50;0,10;2)=0,07794\)
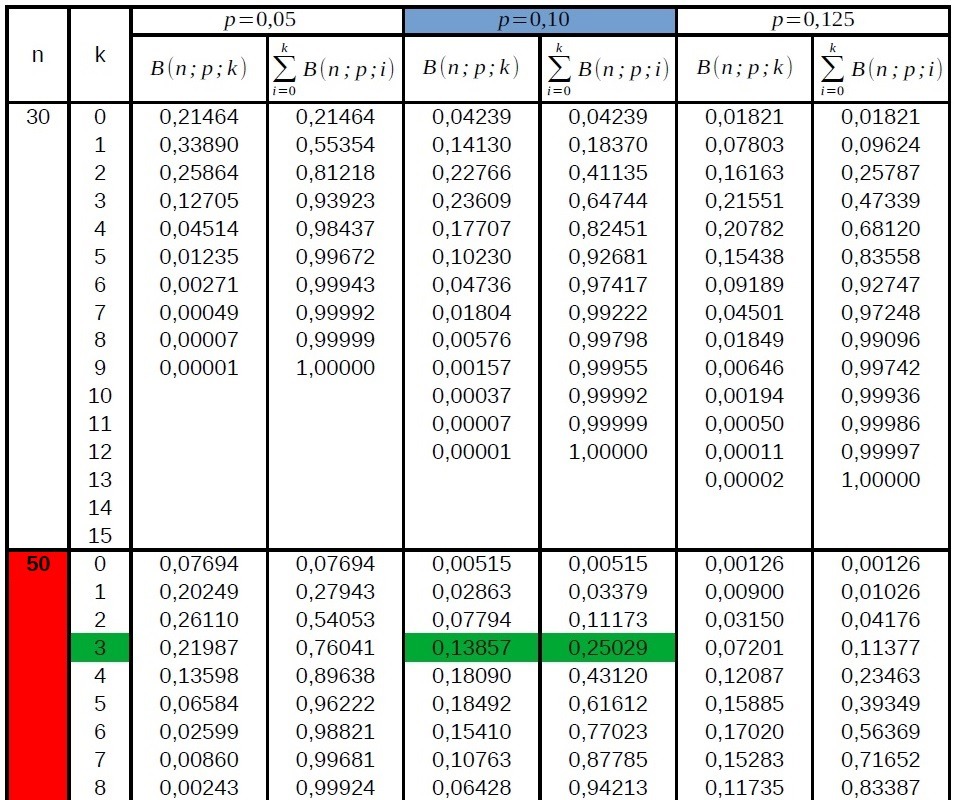
Beispiel für kumulierte Wahrscheinlichkeit:
gegeben: \(p = 0,10, n = 50\)
gesucht: aufsummierte WK für \(0\) bis \(3\) Treffer
Ablesen in der Tabelle im Tafelwerk (rechte Spalte): \(P(T \leq 3) = 0,25029\)
Testen Sie Ihr Können bei den folgenden Übungen
Übung 1
Übung 2
Verwenden Sie bei den folgenden Übungen das Tafelwerk zur Stochastik.
a) Gegeben ist eine Bernoulli-Kette mit \(n=30\) und \(p=0,10\). Ermitteln Sie die Wahrscheinlichkeit \(P(T=12)\).
b) Ermitteln Sie die Wahrscheinlichkeit für genau \(6\) Treffer in einer Bernoulli-Kette der Länge \(50\) mit Treffer-WK \(0,05\).
c) Ermitteln Sie die Wahrscheinlichkeit für genau \(10\) Treffer in einer Bernoulli-Kette der Länge \(30\) mit Treffer-WK \(0,10\).
d) Gegeben ist eine Bernoulli-Kette mit \(n=30\) und \(p=0,10\). Ermitteln Sie die Wahrscheinlichkeit \(P(T \leq 9)\).
e) Ermitteln Sie die aufsummierte Wahrscheinlichkeit für \(0\) bis \(5\) Treffer in einer Bernoulli-Kette der Länge \(50\) mit Treffer-WK \(0,05\).
f) Ermitteln Sie die kumulierte Wahrscheinlichkeit für weniger als \(9\) Treffer in einer Bernoulli-Kette der Länge \(50\) mit Treffer-WK \(0,10\).