Zufallsexperimente
Grundlagen
Die Grundlage der Zufallslehre (Stochastik) liegt darin, dass es manche Prozesse gibt, bei denen vor der Durchführung nicht vorhergesagt werden kann, welchen Ausgang der Prozess nehmen wird. Solche Prozesse heißen deshalb Zufallsexperimente. Damit ein Prozess mathematisch als Zufallsexperiment angesehen wird, müssen drei Bedingungen erfüllt sein:
Definition: Zufallsexperiment
- Das Experiment muss unter identischen Bedingungen beliebig oft wiederholbar sein.
- Die möglichen Ausgänge des Experiments müssen bekannt sein.
- Der genaue Ausgang der nächsten Durchführung kann nicht vorhergesagt werden.
Ein einfaches Beispiel für ein Zufallsexperiment ist das Werfen einer Münze. Die drei Bedingungen sind hierbei offensichtlich erfüllt:
- Die verwendete Münze kann beliebig oft geworfen werden.
- Bei jedem Münzwurf sind die Ausgänge Zahl \((Z)\) und Wappen \((W)\) (manchmal auch als Kopf \((K)\) bezeichnet) möglich.
- Bevor man die Münze wirft kann man nicht angeben, ob die Münze Zahl oder Wappen zeigen wird.
Entscheiden Sie jeweils, ob es sich bei den folgenden Vorgängen um ein Zufallsexperiment handelt oder nicht:
Aufgabe
Entscheiden Sie, ob es sich bei den folgenden Vorgängen jeweils um ein Zufallsexperiment handelt oder nicht. Geben Sie gegebenenfalls auch die möglichen Ausgänge des Experiments an.
- Ein sechsseitiger Würfel wird einmal geworfen.
- Ein Ball wird fallen gelassen.
- Ein Buch wird fallen gelassen und die Seitenzahlen die aufgeschlagen sind werden notiert.
Ergebnis und Ergebnisraum
Um Zufallsexperimente formal genauer beschreiben zu können, benötigen wir eine weitere Definition.
Definition: Ergebnis und Ergebnisraum
Die möglichen Ausgänge eines Zufallsexperiments heißen Ergebnisse. Wir verwenden hierfür das Symbol \(\omega\) (kleines griechisches Omega) und nummerieren diese von \(\omega_1\) bis \(\omega_n\), wobei \(n\) die Anzahl der Ergebnisse ist. Die Menge aller Ergebnisse heißt Ergebnisraum. Dieser wird mit \(\Omega\) (großes griechisches Omega) bezeichnet und es gilt \(\Omega=\{\omega_1;\omega_2;…;\omega_n\}\). Als Mächtigkeit des Ergebnisraums bezeichnet man die Anzahl der Elemente in \(\Omega\) und schreibt \(\vert \Omega \vert \). Hier wäre \(\vert \Omega \vert =n\).
Wenden wir dies auf ein das einmalige Werfen einer Münze (mögliche Ausgänge: Zahl und Wappen) an, so erhalten wir:
\[\omega_1 = Z, \omega_2 =W \Rightarrow \Omega=\, \vert \Omega \vert =2\]
Anmerkung: Die Reihenfolge der Benennung der Ergebnisse ist genau wie die Reihenfolge des Notierens der Ergebnisse im Ergebnisraum beliebig. Eine Systematik (Sortieren von kleinen zu großen Zahlen, Beibehalten der Reihenfolge des Aufgabentexts,…) kann zum Nachvollziehen von Aufgaben aber hilfreich sein.
Aufgabe
Geben Sie zu den folgenden Zufallsexperimenten jeweils die Ergebnisse \(\omega\), sowie den Ergebnisraum \(\Omega\) und dessen Mächtigkeit \(\vert\Omega\vert\) an.
- Werfen eines sechsseitigen Würfels.
- Ziehen eines Loses auf dem Volksfest, bei dem es Gewinne und Nieten gibt.
- Ziehen einer Kugel aus einem Beutel, in dem rote \((r)\), blaue \((b)\) und grüne \((g)\) Kugeln sind.
Baumdiagramme
Die Ergebnisse und der Ergebnisraum dieser einfachen Zufallsexperiments konnten ohne viel Aufwand einfach angegeben werden. Für kompliziertere Zufallsexperimente (z.B. mehrere Zufallsexperimente, die nacheinander ausgeführt werden. Man spricht von mehrstufigen Zufallsexperimenten) kann man sich mit einem Baumdiagramm helfen. Hierbei wird an jeder Verästelung untersucht, welche Ergebnisse im nächsten Schritt auftreten können. Jeder Pfad vom Startpunkt bis zu einem Ende des Baumes repräsentiert dann ein Ergebnis des Zufallsexperiments.
Beispiel: Zweimaliges Werfen einer Münze
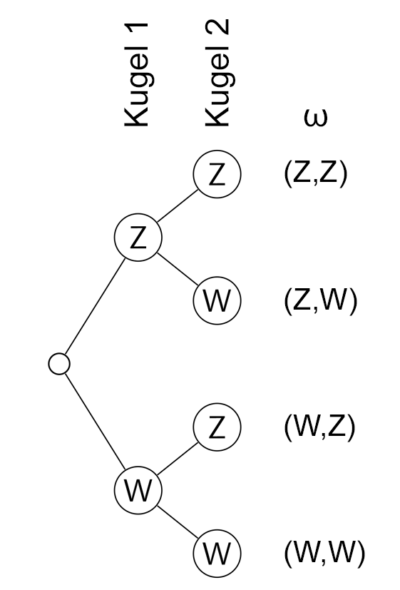
Um auch bei komplizierteren Baumdiagrammen den Überblick zu behalten notiert man z.B. oberhalb der jeweiligen Stufe kurz wofür diese steht. In einer weiteren Spalte hinter dem Baumdiagramm notiert man das zum entsprechenden Pfad gehörende Ergebnis \(\omega\).
Jedes Ergebnis besteht hier also aus zwei Teilen: dem Ergebnis des ersten Münzwurfs und dem des zweiten. Diese bilden zusammen ein Tupel, welches üblicherweise in runden Klammern notiert wird, beispielsweise \((Z,W)\), wenn der erste Münzwurf Zahl und der zweite Wappen ergeben hat. Die Reihenfolge ist bei einem Tupel von Bedeutung, also \((Z,W)\ne (W,Z)\).
Die Ergebnisse sind nun also:
\[\omega_1=(Z,Z), \omega_2=(Z,W), \omega_3=(W,Z), \omega_4=(W,W)\]
und folglich
\[\Omega=\{(Z,Z);(Z,W);(W,Z);(W,W)\}, \vert \Omega \vert =4\]
In manchen Situationen interessiert lediglich, welche Ausgänge aufgetreten sind und nicht in welcher Reihenfolge. Man ersetzt dann die Tupel entweder durch Mengen \((Z,W)\rightarrow \{Z,W\}\) oder lässt die Klammern komplett weg \( (Z,W)\rightarrow ZW\). Dies hat offensichtlich Einfluss auf den Ergebnisraum, denn nun ist \(\Omega =\{ZZ;ZW;WW\}\) und \(\vert\Omega\vert =3\).
Man spricht hierbei von einer Vergröberung des Ergebnisraums, da mehrere Elemente des ursprünglichen Ergebnisraums im neuen Ergebnisraum zusammenfallen. Umgekehrt spricht man von einer Verfeinerung des Ergebnisraum, wenn ein Element des Ergebnisraums in mehrere zerlegt wird (hier also z.B. der Übergang zurück von \(ZW\) zu \( (Z,W) \text{ und }(W,Z) \). Ein Ergebnisraum, bei dem eine weitere Verfeinerung nicht möglich ist, heißt feinster Ergebnisraum.
Wichtig ist, dass nicht ein Ergebnis des Zufallsexperiments mehreren Elemente des Ergebnisraums zugeordnet wird oder aber überhaupt kein passendes Element des Ergebnisraum vorkommt. Für den zweimaligen Münzwurf unzulässige Ergebnisräume wären beispielsweise \(\Omega_1 =\{ZZ;ZW;\text{gleicher Ausgang bei beiden Würfen}\}\) sowie \(\Omega_2=\{(Z,Z);(Z,W);(W,W)\}\).
Aufgabe
- Begründen Sie, weshalb die obigen Ergebnisräume \(\Omega_1\) und \(\Omega_2\) keine zulässigen Ergebnisräume des einmaligen Münzwurfs sind.
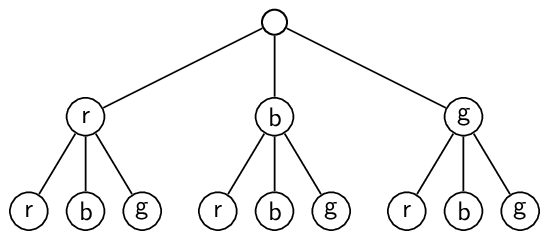
- In einem Beutel befinden sich rote \((r)\), blaue \((b)\) und grüne \((g)\) Kugeln. Es werden nacheinander zwei Kugeln aus dem Beutel gezogen. Fertigen Sie ein passendes Baumdiagramm an und geben Sie anschließend den feinsten Ergebnisraum \(\Omega\) und \(\vert\Omega\vert \) an.
- Geben Sie zum zweimaligen Würfeln den feinsten Ergebnisraum und dessen Mächtigkeit an. Nutzen Sie falls nötig …, um den Schreibaufwand zu minimieren.
- Beim Gesellschaftsspiel „Mensch ärgere dich nicht“ ist zu Beginn des Spiels zunächst nur entscheidend, ob die Augenzahl \(6\) gewürfelt wird oder nicht. Hierfür hat ein Spieler drei Versuche. Fällt in einem der drei Würfe die Augenzahl \(6\), so darf der Spieler ein weiteres Mal würfeln und die gewürfelte Augenzahl ziehen.
- Geben Sie einen Ergebnisraum für die bis zu drei Versuche eine \(6\) zu würfeln an.
- Geben Sie einen Ergebnisraum für den zusätzlichen Würfelwurf an, der entscheidet, wie weit der Spieler ziehen darf.
- Kombinieren Sie die beiden Ergebnisräume, um den gesamten Prozess der bis zu vier Würfelwürfe wiederzugeben. Geben Sie den Gesamtergebnisraum an. Hinweis: Der zweite Ergebnisraum kommt nur dann zum Einsatz, wenn erstmalig eine 6 gewürfelt wurde.
Wirft man in beiden Würfen das Ergebnis Zahl, so kommt im Ergebnisraum \(\Omega_1\) sowohl \(ZZ\) als auch \(\text{gleicher Ausgang bei beiden Würfen}\) in Frage.
Da bei \(\Omega_2\) die Reihenfolge der Ausgänge beachtet wird (Tupel), fehlt das Element \((W,Z)\).
\(\Omega=\{(r,r);(r,b);(r,g);(b,r);(b,b);(b,g);(g,r);(g,b);(g,g)\}, \vert \Omega \vert =9 \)
\( \begin{array} {lll}\Omega=\{ & (1,1), (1,2), … , (1,6),& \\ & (2,1), (2,2), … , (2,6),& \\ & \vdots & \\ & (6,1), (6,2), … , (6,6)&\} \\ \end{array} \)
\(\vert\Omega\vert =36\)
\(\Omega_1 = \{(6);(n6,6);(n6,n6,6);(n6,n6,n6)\}\)
Hierbei steht \(n6\) für „nicht \(6\)“, da für den Spieler egal ist, welche Augenzahl gewürfelt wird, solange es nicht die Augenzahl \(6\) ist.
\(\Omega_2=\{1;2;3;4;5;6\}\)
Da nun entschieden wird, wie weit der Spieler ziehen darf, muss nun jede Augenzahl einzeln betrachtet werden.
Wir kombinieren die beiden Ergebnisräume aus 4a und 4b, indem wir \(\Omega_2\) jedes Mal dann anfügen, wenn bei der Unterscheidung \(6\) oder \(n6\) die Augenzahl \(6\) gefallen ist. Damit gibt es folgenden Gesamtergebnisraum:
\(\begin{array}{ll} \Omega=\{ &\overbrace{(6,1);(6,2);…;(6,6)}^{\substack{\text{6 im ersten Wurf,}\\ \text{danachAugenzahlen 1 bis 6}}};\overbrace{(n6,6,1);(n6,6,2);…;(n6,6,6)}^{\substack{\text{n6 im ersten Wurf,}\\ \text{6 im zweiten Wurf,} \\ \text{danach Augenzahlen 1 bis 6}}};&\\ &\underbrace{(n6,n6,6,1);(n6,n6,6,2);…;(n6,n6,6,6)}_{\substack{\text{n6 im ersten Wurf,}\\ \text{n6 im zweiten Wurf,} \\ \text{6 im dritten Wurf,} \\ \text{danach Augenzahlen 1 bis 6}}};(n6;n6;n6) &\}\end{array}\)