Thermodynamische Prozesse
Zustandsdiagramme
Komplexe thermodynamische Vorgänge, wie sie sich beispielsweise in Verbrennungsmotoren abspielen, lassen sich aus einfachen thermodynamischen Prozessen zusammensetzen und damit näherungsweise beschreiben. Erst dadurch wird es möglich diese Vorgänge zu untersuchen und zu optimieren. Deshalb werden im folgenden die grundlegenden thermodynamischen Prozesse behandelt und grafisch in Zustandsdiagrammen dargestellt.
Isobarer Prozess
Hier handelt es sich um eine Zustandsänderung eines Gases von einem Zustand 1 in einen Zustand 2, wobei der Gasdruck während des Prozesses konstant bleibt. Damit der Druck während der Prozessführung von 1 zu 2 gleich bleibt, muss die von außen auf den Kolben wirkende Kraft konstant gehalten werden.
Den Zustand eines Systems stellt man in einem Diagramm dar, dem p(V)- oder Zustandsdiagramm. Ein Gas in einem Zustand 1 hat ein bestimmtes Volumen V1 und einen Druck p1. Dieser Zustand wird als Punkt 1 in das Zustandsdiagramm eingetragen. Im Zustand 2 hat das Gas ein anderes Volumen V2 und den Druck p2, der im Falle isobarer Prozessführung den gleichen Wert hat wie im Zustand 1. Man erhält dafür einen Punkt 2, der auf der gleichen Höhe liegt wie der Punkt 1.
Die Kurve, in diesem Falle ist es ein Geradenstück, zwischen den Zuständen 1 und 2 im Zustandsdiagramm stellt die Zustände des Gases während des Prozesses dar. Da im hier dargestellten Prozess der Druck konstant bleibt, bezeichnet man diese Prozesskurve als Isobare. Auch der Wärmeumsatz wird in das Zustandsdiagramm eingetragen.
Während des Prozessverlaufes verrichtet das Gas Arbeit, indem es den Kolben gegen die von außen einwirkende Kraft F um Ds verschiebt. Das Gasvolumen vergrößert sich dabei um
V = V2 – V1
V = A ·
s,
wobei A die Querschnittsfläche des Kolbens ist. Zur Berechnung dieser Arbeit werden folgende Überlegungen angestellt:
| Für die Arbeit gilt ganz allgemein: | W = F · |
| Die Formel für den Druck lautet: | p = F/A das ergibt umgestellt: F = p · A |
| Eingesetzt in die Arbeitsformel folgt: | W = p · A · |
Der Wert des Ausdrucks p · V ist anderseits (rein geometrisch) der Flächeninhalt des Rechtecks unter der Isobaren. Demnach ist die während des Prozesses zwischen den Zuständen 1 und 2 umgesetzte Arbeit W12 im Zustandsdiagramm der Inhalt der Fläche unter der Prozesskurve. Eine Korrektur an dem Ergebnis muss noch vorgenommen werden: Die Formel liefert bei Arbeitsabgabe (Expansion des Gases, also
V = V2 – V1 > 0) einen positiven Wert, bei Zufuhr von Arbeit einen negativen Wert. Die Vorzeichenvereinbarung für zugeführte/abgegebene Arbeit ist aber genau umgekehrt. Durch ein negatives Vorzeichen in der Formel wird das korrigiert.
Die zwischen den Zuständen 1 und 2 umgesetzte Arbeit W12 eines isobaren Prozesses ergibt sich wie folgt:
W12 = – V = – p·(V2 – V1)
Isochorer Prozess
Bei isochoren Prozessen wird keine Arbeit umgesetzt, da der Kolben festgehalten wird. Es gilt also:
W12 = 0
Wie der Abbildung zu entnehmen ist, existiert unter der isochoren Prozesskurve auch keine Fläche. Demzufolge gilt auch bei isochoren Prozessen, dass der Flächeninhalt unter der Prozesskurve dem Betrag der umgesetzten Arbeit entspricht.
Die zwischen den Zuständen 1 und 2 zugeführte Wärme Q12 geht nicht verloren (Energieerhaltungssatz!), sondern erhöht die im Gas gespeicherte Energie. Man nennt sie innere Energie und bezeichnet sie mit U. Die innere Energie ist wie das Volumen, der Druck und die Temperatur eine Zustandsgröße, die den Zustand des Gases charakterisiert. Sie hat im Zustand 1 einen bestimmten Wert; er wird mit U1 bezeichnet, entsprechend wird der Wert im Zustand 2 mit U2 gekennzeichnet. Da die zugeführte Wärme allein zur Veränderung der inneren Energie verwendet wird, muss nach dem Energieerhaltungssatz gelten:
U = Q12
Anmerkung: Das Differenzsymbol wird nur bei Zustandsgrößen verwendet, da nur diese einen eindeutigen Wert im Zustand 1 und im Zustand 2 besitzen, so dass diese Differenz berechnet werden kann. Bei den systemgrenzenüberschreitenden Größen W und Q ist eine Differenzbildung nicht möglich, da diese keinen bestimmten Wert in den Zuständen 1 und 2 besitzen. Der Doppelindex 12 bezeichnet hier die Menge der zwischen den Zuständen 1 und 2 übertragenen Energie Arbeit oder Wärme.
Isothermer Prozess
Im Zustandsdiagramm sind die Kurven konstanter Temperatur, die Isothermen, Hyperbeläste, wie das Gesetz von Boyle-Mariotte p·V = konstant zeigt. Je höher die konstante Temperatur gewählt wird, umso weiter nach oben verschiebt sich die zugehörige Isotherme im Diagramm. Dass die Isotherme bei höherer Temperatur weiter oben verläuft, sieht man leicht ein: Bei einem bestimmten festen Volumen hat das Gas mit höherer Temperatur einen höheren Druck; die zugehörige Prozesskurve muss deshalb im Diagramm weiter oben liegen.
Adiabater Prozess
Eine Zustandsänderung ohne Wärmeaustausch mit der Umgebung bezeichnet man als adiabat. Solche Vorgänge hat man beispielsweise bei wärmeisolierten Systemen. Viele Zustandsänderungen in Maschinen laufen adiabat ab, ohne dass eine besondere Wärmeisolierung erforderlich wäre. Diese Vorgänge, wie beispielsweise die Kompression eines Gases in einem Kolbenmotor, erfolgen so schnell, dass keine Zeit zu einem Wärmetausch bleibt. Adiabate Prozesse sind deshalb in der Praxis besonders wichtig.
Wird ein Gas adiabat komprimiert, so steigt – im Gegensatz zu einer isothermen Kompression – die Gastemperatur an. Aufgrund des Temperaturanstiegs steigt bei adiabater Prozessführung der Druck stärker als bei isothermer. Das zeigt sich in der Zustandsebene durch einen stärkeren Anstieg der Adiabaten im Vergleich zu Isothermen.
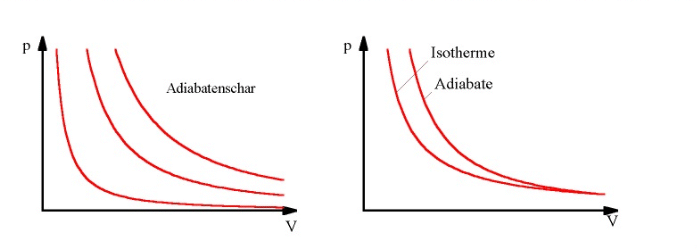
Im rechten Bild erkennt man diesen steileren Anstieg der Adiabaten gegenüber der Isothermen. Bei der adiabaten Zustandsgleichung, die experimentell ermittelt wird, muss der Adiabatenexponenten (kappa) eingeführt werden. Dabei handelt es sich um eine dimensionslose Zahl zwischen 1 und 1,67. Ihr Wert hängt von der Gasart ab und beträgt beispielsweise für Luft
= 1,40. Die wichtige Adiabatengleichung lautet:
Diese adiabate Zustandsgleichung unterscheidet sich von der isothermen pV = konst. nur durch den Adiabatenexponenten k. Mit Hilfe der allgemeinen Gasgleichung können aus obiger Zustandsgleichung eine Reihe weiterer, daraus abgeleiteter Adiabatengleichungen gewonnen werden:
Mit diesen Gleichungen ergeben sich die Zusammenhänge zwischen T und p, zwischen T und V sowie zwischen p und V.
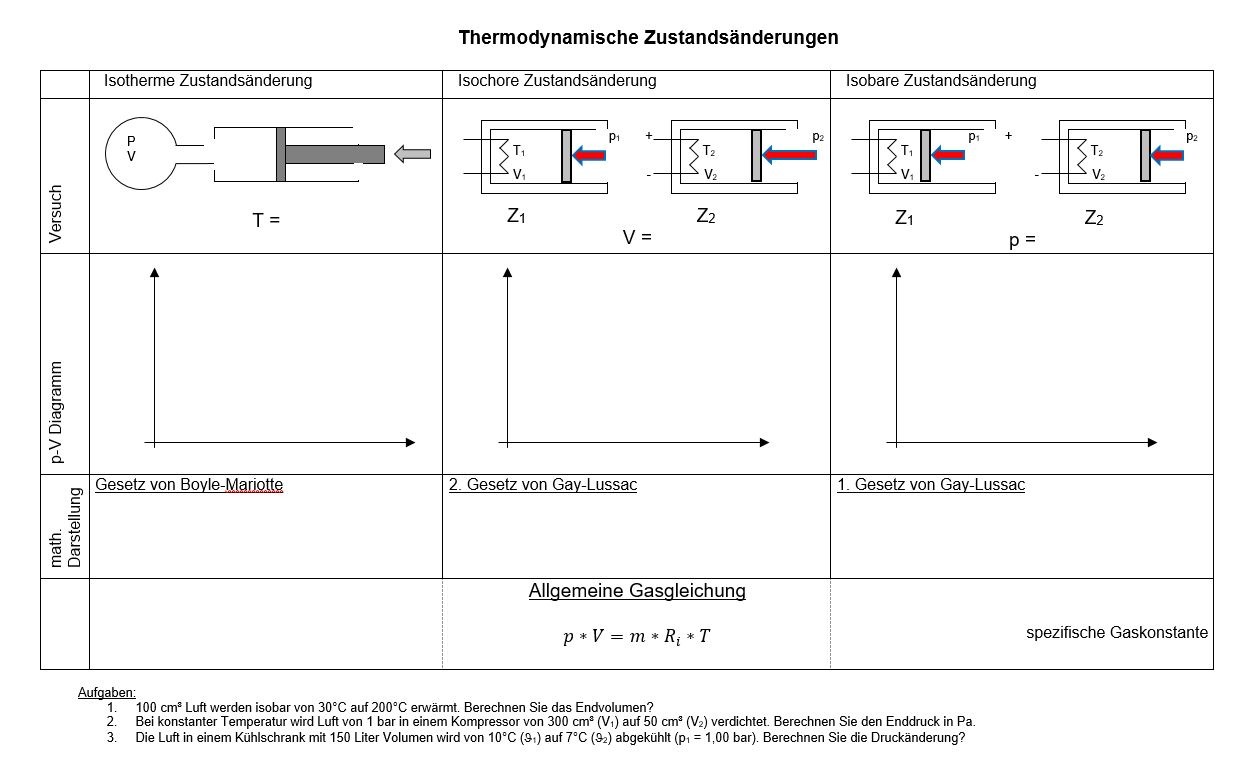
Die drei Zustandsänderungen isotherm, isochor und isobar sind in dem AB Thermodynamische Zustandsänderungen zusammengefasst: